
In elementary algebra, a trinomial is a polynomial consisting of three terms or monomials. [1]

In elementary algebra, a trinomial is a polynomial consisting of three terms or monomials. [1]
A trinomial equation is a polynomial equation involving three terms. An example is the equation studied by Johann Heinrich Lambert in the 18th century. [2]

In mathematics, a Diophantine equation is an equation, typically a polynomial equation in two or more unknowns with integer coefficients, for which only integer solutions are of interest. A linear Diophantine equation equates to a constant the sum of two or more monomials, each of degree one. An exponential Diophantine equation is one in which unknowns can appear in exponents.
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

Elementary algebra, also known as college algebra, encompasses the basic concepts of algebra. It is often contrasted with arithmetic: arithmetic deals with specified numbers, whilst algebra introduces variables.
In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.
In algebra, a quadratic equation is any equation that can be rearranged in standard form as
In mathematics, a coefficient is a multiplicative factor involved in some term of a polynomial, a series, or an expression. It may be a number (dimensionless), in which case it is known as a numerical factor. It may also be a constant with units of measurement, in which it is known as a constant multiplier. In general, coefficients may be any expression. When the combination of variables and constants is not necessarily involved in a product, it may be called a parameter.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.
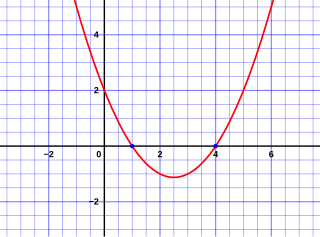
In elementary algebra, the quadratic formula is a formula that provides the two solutions, or roots, to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as completing the square.

In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is an integer factorization of 15, and (x – 2)(x + 2) is a polynomial factorization of x2 – 4.

In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic".
In mathematics, a quadratic form is a polynomial with terms all of degree two. For example,

In mathematics, a quintic function is a function of the form
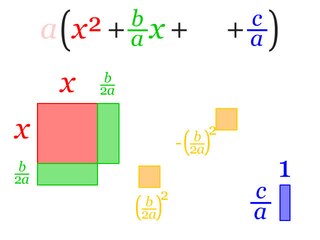
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the form

In algebra, a quartic function is a function of the form
In mathematics, a monomial is, roughly speaking, a polynomial which has only one term. Two definitions of a monomial may be encountered:
In mathematics, an algebraic equation or polynomial equation is an equation of the form , where P is a polynomial with coefficients in some field, often the field of the rational numbers. For example, is an algebraic equation with integer coefficients and
In algebra, a binomial is a polynomial that is the sum of two terms, each of which is a monomial. It is the simplest kind of a sparse polynomial after the monomials.
In mathematics, a variable is a symbol that represents a mathematical object. A variable may represent a number, a vector, a matrix, a function, the argument of a function, a set, or an element of a set.
In mathematics, an algebraic expression is an expression built up from constant algebraic numbers, variables, and the algebraic operations. For example, 3x2 − 2xy + c is an algebraic expression. Since taking the square root is the same as raising to the power 1/2, the following is also an algebraic expression:
In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. For a univariate polynomial, the degree of the polynomial is simply the highest exponent occurring in the polynomial. The term order has been used as a synonym of degree but, nowadays, may refer to several other concepts.