variance-gamma distribution| Parameters |  location (real) location (real)
 (real) (real)
 asymmetry parameter (real) asymmetry parameter (real)
 shape parameter (alternative parameterizations use shape parameter (alternative parameterizations use  [1] ) [1] )
 |
|---|
| Support |  |
|---|
| PDF | 
 denotes a modified Bessel function of the second kind denotes a modified Bessel function of the second kind
 denotes the Gamma function denotes the Gamma function |
|---|
| Mean |  |
|---|
| Variance |  |
|---|
| MGF |  |
|---|
The variance-gamma distribution, generalized Laplace distribution [2] or Bessel function distribution [2] is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the gamma distribution. The tails of the distribution decrease more slowly than the normal distribution. It is therefore suitable to model phenomena where numerically large values are more probable than is the case for the normal distribution. Examples are returns from financial assets and turbulent wind speeds. The distribution was introduced in the financial literature by Madan and Seneta. [3] The variance-gamma distributions form a subclass of the generalised hyperbolic distributions.
The fact that there is a simple expression for the moment generating function implies that simple expressions for all moments are available. The class of variance-gamma distributions is closed under convolution in the following sense. If  and
and  are independent random variables that are variance-gamma distributed with the same values of the parameters
are independent random variables that are variance-gamma distributed with the same values of the parameters  and
and  , but possibly different values of the other parameters,
, but possibly different values of the other parameters,  ,
,  and
and 
 , respectively, then
, respectively, then  is variance-gamma distributed with parameters
is variance-gamma distributed with parameters  ,
,  ,
,  and
and  .
.
The variance-gamma distribution can also be expressed in terms of three inputs parameters (C,G,M) denoted after the initials of its founders. If the "C",  here, parameter is integer then the distribution has a closed form 2-EPT distribution. See 2-EPT Probability Density Function. Under this restriction closed form option prices can be derived.
here, parameter is integer then the distribution has a closed form 2-EPT distribution. See 2-EPT Probability Density Function. Under this restriction closed form option prices can be derived.
If  ,
,  and
and  , the distribution becomes a Laplace distribution with scale parameter
, the distribution becomes a Laplace distribution with scale parameter  . As long as
. As long as  , alternative choices of
, alternative choices of  and
and  will produce distributions related to the Laplace distribution, with skewness, scale and location depending on the other parameters. [4]
will produce distributions related to the Laplace distribution, with skewness, scale and location depending on the other parameters. [4]
For a symmetric variance-gamma distribution, the kurtosis can be given by  . [1]
. [1]
See also Variance gamma process.

In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.

In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] or in terms of two positive parameters, denoted by alpha (α) and beta (β), that appear as exponents of the variable and its complement to 1, respectively, and control the shape of the distribution.
In Bayesian probability theory, if the posterior distribution is in the same probability distribution family as the prior probability distribution , the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood function .

In probability theory and statistics, the Laplace distribution is a continuous probability distribution named after Pierre-Simon Laplace. It is also sometimes called the double exponential distribution, because it can be thought of as two exponential distributions spliced together along the abscissa, although the term is also sometimes used to refer to the Gumbel distribution. The difference between two independent identically distributed exponential random variables is governed by a Laplace distribution, as is a Brownian motion evaluated at an exponentially distributed random time. Increments of Laplace motion or a variance gamma process evaluated over the time scale also have a Laplace distribution.

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.

The Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.

In probability theory and statistics, the generalized inverse Gaussian distribution (GIG) is a three-parameter family of continuous probability distributions with probability density function
The generalised hyperbolic distribution (GH) is a continuous probability distribution defined as the normal variance-mean mixture where the mixing distribution is the generalized inverse Gaussian distribution (GIG). Its probability density function is given in terms of modified Bessel function of the second kind, denoted by . It was introduced by Ole Barndorff-Nielsen, who studied it in the context of physics of wind-blown sand.
The normal-inverse Gaussian distribution is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the inverse Gaussian distribution. The NIG distribution was noted by Blaesild in 1977 as a subclass of the generalised hyperbolic distribution discovered by Ole Barndorff-Nielsen. In the next year Barndorff-Nielsen published the NIG in another paper. It was introduced in the mathematical finance literature in 1997.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
In probability theory and statistics, the normal-gamma distribution is a bivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and precision.
The Birnbaum–Saunders distribution, also known as the fatigue life distribution, is a probability distribution used extensively in reliability applications to model failure times. There are several alternative formulations of this distribution in the literature. It is named after Z. W. Birnbaum and S. C. Saunders.

In probability theory and statistics, the normal-inverse-gamma distribution is a four-parameter family of multivariate continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and variance.

In the theory of stochastic processes, a part of the mathematical theory of probability, the variance gamma process (VG), also known as Laplace motion, is a Lévy process determined by a random time change. The process has finite moments distinguishing it from many Lévy processes. There is no diffusion component in the VG process and it is thus a pure jump process. The increments are independent and follow a variance-gamma distribution, which is a generalization of the Laplace distribution.
The generalized normal distribution or generalized Gaussian distribution (GGD) is either of two families of parametric continuous probability distributions on the real line. Both families add a shape parameter to the normal distribution. To distinguish the two families, they are referred to below as "symmetric" and "asymmetric"; however, this is not a standard nomenclature.
A geometric stable distribution or geo-stable distribution is a type of leptokurtic probability distribution. Geometric stable distributions were introduced in Klebanov, L. B., Maniya, G. M., and Melamed, I. A. (1985). A problem of Zolotarev and analogs of infinitely divisible and stable distributions in a scheme for summing a random number of random variables. These distributions are analogues for stable distributions for the case when the number of summands is random, independent of the distribution of summand, and having geometric distribution. The geometric stable distribution may be symmetric or asymmetric. A symmetric geometric stable distribution is also referred to as a Linnik distribution. The Laplace distribution and asymmetric Laplace distribution are special cases of the geometric stable distribution. The Mittag-Leffler distribution is also a special case of a geometric stable distribution.

The Lomax distribution, conditionally also called the Pareto Type II distribution, is a heavy-tail probability distribution used in business, economics, actuarial science, queueing theory and Internet traffic modeling. It is named after K. S. Lomax. It is essentially a Pareto distribution that has been shifted so that its support begins at zero.
In probability theory and statistics, the noncentral beta distribution is a continuous probability distribution that is a noncentral generalization of the (central) beta distribution.
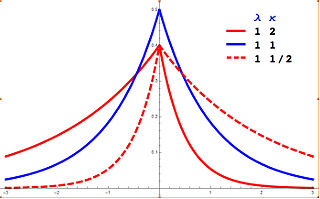
In probability theory and statistics, the asymmetric Laplace distribution (ALD) is a continuous probability distribution which is a generalization of the Laplace distribution. Just as the Laplace distribution consists of two exponential distributions of equal scale back-to-back about x = m, the asymmetric Laplace consists of two exponential distributions of unequal scale back to back about x = m, adjusted to assure continuity and normalization. The difference of two variates exponentially distributed with different means and rate parameters will be distributed according to the ALD. When the two rate parameters are equal, the difference will be distributed according to the Laplace distribution.





































