
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation
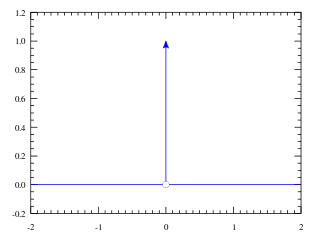
In mathematical analysis, the Dirac delta function, also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Since there is no function having this property, to model the delta "function" rigorously involves the use of limits or, as is common in mathematics, measure theory and the theory of distributions.
In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state that has dynamics most closely resembling the oscillatory behavior of a classical harmonic oscillator. It was the first example of quantum dynamics when Erwin Schrödinger derived it in 1926, while searching for solutions of the Schrödinger equation that satisfy the correspondence principle. The quantum harmonic oscillator arise in the quantum theory of a wide range of physical systems. For instance, a coherent state describes the oscillating motion of a particle confined in a quadratic potential well. The coherent state describes a state in a system for which the ground-state wavepacket is displaced from the origin of the system. This state can be related to classical solutions by a particle oscillating with an amplitude equivalent to the displacement.
Fourier optics is the study of classical optics using Fourier transforms (FTs), in which the waveform being considered is regarded as made up of a combination, or superposition, of plane waves. It has some parallels to the Huygens–Fresnel principle, in which the wavefront is regarded as being made up of a combination of spherical wavefronts whose sum is the wavefront being studied. A key difference is that Fourier optics considers the plane waves to be natural modes of the propagation medium, as opposed to Huygens–Fresnel, where the spherical waves originate in the physical medium.
In computational chemistry and molecular physics, Gaussian orbitals are functions used as atomic orbitals in the LCAO method for the representation of electron orbitals in molecules and numerous properties that depend on these.

In mathematics, the polylogarithm (also known as Jonquière's function, for Alfred Jonquière) is a special function Lis(z) of order s and argument z. Only for special values of s does the polylogarithm reduce to an elementary function such as the natural logarithm or a rational function. In quantum statistics, the polylogarithm function appears as the closed form of integrals of the Fermi–Dirac distribution and the Bose–Einstein distribution, and is also known as the Fermi–Dirac integral or the Bose–Einstein integral. In quantum electrodynamics, polylogarithms of positive integer order arise in the calculation of processes represented by higher-order Feynman diagrams.
Geometrical optics, or ray optics, is a model of optics that describes light propagation in terms of rays. The ray in geometrical optics is an abstraction useful for approximating the paths along which light propagates under certain circumstances.
In mathematics, the Helmholtz equation is the eigenvalue problem for the Laplace operator. It corresponds to the linear partial differential equation
In mathematics, the Hankel transform expresses any given function f(r) as the weighted sum of an infinite number of Bessel functions of the first kind Jν(kr). The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r axis. The necessary coefficient Fν of each Bessel function in the sum, as a function of the scaling factor k constitutes the transformed function. The Hankel transform is an integral transform and was first developed by the mathematician Hermann Hankel. It is also known as the Fourier–Bessel transform. Just as the Fourier transform for an infinite interval is related to the Fourier series over a finite interval, so the Hankel transform over an infinite interval is related to the Fourier–Bessel series over a finite interval.
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.

The Wigner quasiprobability distribution is a quasiprobability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics. The goal was to link the wavefunction that appears in Schrödinger's equation to a probability distribution in phase space.

In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field configurations. Any two detailed configurations in the same equivalence class are related by a certain transformation, equivalent to a shear along unphysical axes in configuration space. Most of the quantitative physical predictions of a gauge theory can only be obtained under a coherent prescription for suppressing or ignoring these unphysical degrees of freedom.
In physics, the optical theorem is a general law of wave scattering theory, which relates the zero-angle scattering amplitude to the total cross section of the scatterer. It is usually written in the form
In optics, the Fresnel diffraction equation for near-field diffraction is an approximation of the Kirchhoff–Fresnel diffraction that can be applied to the propagation of waves in the near field. It is used to calculate the diffraction pattern created by waves passing through an aperture or around an object, when viewed from relatively close to the object. In contrast the diffraction pattern in the far field region is given by the Fraunhofer diffraction equation.
The Sommerfeld identity is a mathematical identity, due Arnold Sommerfeld, used in the theory of propagation of waves,
In physics, the plane-wave expansion expresses a plane wave as a linear combination of spherical waves:
In physics and mathematics, the spacetime triangle diagram (STTD) technique, also known as the Smirnov method of incomplete separation of variables, is the direct space-time domain method for electromagnetic and scalar wave motion.
In optics, the Ewald–Oseen extinction theorem, sometimes referred to as just the extinction theorem, is a theorem that underlies the common understanding of scattering. It is named after Paul Peter Ewald and Carl Wilhelm Oseen, who proved the theorem in crystalline and isotropic media, respectively, in 1916 and 1915. Originally, the theorem applied to scattering by an isotropic dielectric objects in free space. The scope of the theorem was greatly extended to encompass a wide variety of bianisotropic media.
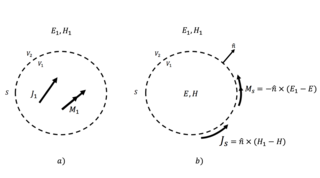
In electromagnetism, surface equivalence principle or surface equivalence theorem relates an arbitrary current distribution within an imaginary closed surface with an equivalent source on the surface. It is also known as field equivalence principle, Huygens' equivalence principle or simply as the equivalence principle. Being a more rigorous reformulation of the Huygens–Fresnel principle, it is often used to simplify the analysis of radiating structures such as antennas.

The method of moments (MoM), also known as the moment method and method of weighted residuals, is a numerical method in computational electromagnetics. It is used in computer programs that simulate the interaction of electromagnetic fields such as radio waves with matter, for example antenna simulation programs like NEC that calculate the radiation pattern of an antenna. Generally being a frequency-domain method, it involves the projection of an integral equation into a system of linear equations by the application of appropriate boundary conditions. This is done by using discrete meshes as in finite difference and finite element methods, often for the surface. The solutions are represented with the linear combination of pre-defined basis functions; generally, the coefficients of these basis functions are the sought unknowns. Green's functions and Galerkin method play a central role in the method of moments.












