Allais effect

Last updated
Allais' paraconical pendulum Litbourgeot.jpg
Allais' paraconical pendulum
Photo taken during the French 1999 eclipse Solar eclipse 1999 4.jpg
Photo taken during the French 1999 eclipse

The Allais effect is the alleged anomalous behavior of pendulums or gravimeters which is sometimes purportedly observed during a solar eclipse. The effect was first reported as an anomalous precession of the plane of oscillation of a Foucault pendulum during the solar eclipse of June 30, 1954 by Maurice Allais, a French polymath who later won the Nobel Prize in Economics. [1] Allais reported another observation of the effect during the solar eclipse of October 2, 1959 using the paraconical pendulum he invented. [2] [3] This study earned him the 1959 Galabert Prize of the French Astronautical Society and made him a laureate of the U.S. Gravity Research Foundation for his 1959 memoir on gravity. [4] The veracity of the Allais effect remains controversial among the scientific community, as its testing has frequently met with inconsistent or ambiguous results over more than five decades of observation.

Contents

Experimental observations

Maurice Allais emphasized the "dynamic character" of the effects he observed: [5]

The observed effects are only seen when the pendulum is moving. They are not connected with the intensity of weight (gravimetry), but with the variation of weight (or of inertia) in the space swept by the pendulum. Actually, while the movement of the plane of oscillation of the pendulum is inexplicable by the theory of gravitation, the deviations from the vertical are explained perfectly by that theory. The deviations from the vertical […] correspond to a static phenomenon, while my experiments correspond to a dynamic phenomenon.

Besides Allais' own experiments, related research about a possible effect of the Moon's shielding, absorption or bending of the Sun's gravitational field during a solar eclipse have been conducted by scientists around the world. Some observations have yielded positive results, seemingly confirming that minute but detectable variations in the expected behavior of devices dependent on gravity do indeed occur within the umbra of an eclipse, but others have failed to detect any noticeable effect.

Anomalous results

Romanian physicist Gheorghe Jeverdan et al. observed the Allais effect and the so-called Jeverdan-Rusu-Antonescu effect or Jeverdan effect (i.e. the change in the oscillation period of a pendulum during an eclipse) while monitoring a Foucault pendulum during the solar eclipse of February 15, 1961. The authors made two hypotheses regarding their observation: during an eclipse, the Moon exerts a screening effect on the gravitational attraction of the Sun so that the attraction of the Earth is indirectly increased, a phenomenon that could also be studied with tides. If the hypothesis of the screening effect is wrong, another explanation could be that the variation of the Earth's gravity might be considered as a result of the diffraction of gravitational waves. [6] [7] Erwin Saxl and Mildred Allen similarly reported strong anomalous changes in the period of a torsion pendulum during the solar eclipse of March 7, 1970 and concluded that "gravitational theory needs to be modified". [8]

Dr. Leonid Savrov of the Sternberg Astronomical Institute built a dedicated paraconical pendulum to test the Allais effect during the solar eclipse of July 11, 1991 in Mexico and the eclipse of November 3, 1994 in Brazil. While he could not observe Allais' claim that there is a diurnal periodicity in the motion of a paraconical pendulum, he did, however, write: "The most interesting result of the Mexico and Brazil experiments is the increase of rotational velocity of the pendulum oscillation plane in the direction of the Foucault effect during the eclipse. It seems that we have some kind of special effect." [9] [10] [11] [12]

Various other experiments using atomic clocks and gravimeters instead of pendulums also recorded significant anomalous gravitational effects which can neither be caused by a tidal effect or drift of the gravimeters, nor by high-frequency noise which has special patterns. These experiments were set up by different teams during solar eclipses in China in 1992, [13] India in 1995, [14] and China in 1997. [15]

Results reporting the observation of the Allais and Jeverdan-Rusu-Antonescu effects during the annular solar eclipse of September 22, 2006 were presented the following year by a Romanian team, with a quantization of the behavior of the paraconical pendulum. [16] During the solar eclipse of August 1, 2008, a Ukrainian team and two Romanian teams worked together hundreds of kilometers apart with different apparatuses: five independent miniature torsion balances for the Ukrainian team, two independent short ball-borne pendulums for a Romanian team and a long Foucault pendulum for the third team. All three teams detected unexplained and mutually correlated disturbances. [17] The same teams repeated a dual experiment during the annular solar eclipse of January 26, 2009, this time outside of the umbra, with the same significant correlation between the behavior of light torsion balances and a Foucault pendulum. [18] They also registered similar anomalies using a Foucault pendulum and a very light torsion balance, both located underground in a disused salt mine with minimal interference, during the partial solar eclipse of June 1, 2011.

Inconclusive or negative results

Louis B. Slichter, using a gravimeter during the solar eclipse of February 15, 1961 in Florence, Italy, failed to detect an associated gravitational signal. [19]

During the solar eclipse of July 22, 1990, no anomalous period increase of a torsion pendulum was detected independently by a team in Finland [20] and another team in Belomorsk, USSR. [21]

The total solar eclipse of August 11, 1999 had been a good opportunity to solve a 45-year mystery, thanks to an international collaboration. NASA's Marshall Space Flight Center first inquired about experimental protocols to Maurice Allais, [5] in order to coordinate ahead of the event a worldwide effort to test the Allais effect between observatories and universities over seven countries (United States, Austria, Germany, Italy, Australia, England and four sites in the United Arab Emirates). The lead supervisor then stated: "The initial interpretation of the record points to three possibilities: a systematic error, a local effect, or the unexplored. To eliminate the first two possibilities, we and several other observers will use different kinds of measuring instruments in a distributed global network of observing stations." [22] [23] However, after the eclipse, Allais criticized the experiments in his final NASA report, writing the period of observation was "much too short […] to detect anomalies properly". [5] Moreover, the lead supervisor left NASA shortly thereafter with the gathered data and the NASA study has never been published. [24]

Further observations conducted by the team led by Xin-She Yang appear to have yielded much weaker evidence of anomalies than their first 1997 study. The authors first posited a more conventional explanation based on temperature changes causing ground tilting, but later suggested that this explanation was unlikely. [25] A possible yet controversial explanation was finally proposed by the same author and Tom Van Flandern which conjectured that the anomaly is due to the gravitational effect of an increased air density spot in the upper atmosphere created by cooling winds during the solar eclipse. They conclude there have been "no unambiguous detections [of an Allais effect] within the past 30 years when consciousness of the importance of [experimental] controls was more widespread." They point out that "the gravitation anomaly discussed here is about a factor of 100,000 too small to explain the Allais excess pendulum precession […] during eclipses" and from this conclude that the original Allais anomaly was merely due to poor controls. [26]

Eight gravimeters and two pendulums were deployed across six monitoring sites in China for the solar eclipse of July 22, 2009. [27] Although one of the scientists involved described in an interview having observed the Allais effect, [28] no result has been published in any academic journal. An automated Foucault pendulum was also used during the solar eclipse of July 11, 2010 in Argentina, with no evidence of a precession change of the pendulum's oscillation plane (< 0.3 degree per hour). [29]

Aether hypothesis

Maurice Allais states that the eclipse effect is related to a gravitational anomaly that is inexplicable in the framework of the currently admitted theory of gravitation, without giving any explanation of his own. [30] Allais' explanation for another anomaly (the lunisolar periodicity in variations of the azimuth of a pendulum) is that space evinces certain anisotropic characteristics, which he ascribes to motion through an aether which is partially entrained by planetary bodies.

His hypothesis leads to a speed of light dependent on the moving direction with respect to a terrestrial observer, since the Earth moves within the aether but the rotation of the Moon induces a "wind" of about 8 km/s. Thus Allais rejects Einstein's interpretation of the Michelson–Morley experiment and the subsequent verification experiments of Dayton Miller. [31] [32]

In particular, the Michelson–Morley experiment did not give a zero speed difference, but at most 8 km/s, without being able to detect any regularity. This difference was therefore interpreted as due to measurement uncertainties. Similarly, Miller's experiments corroborated these results over a long period of time, but Miller could not explain the source of the irregularities. At the time, temperature problems were invoked to explain the cause, as concluded by Robert S. Shankland. [33] By re-analyzing the data from this experiment, Allais reported a periodicity using sidereal time rather than civil time used by Miller (daytime sidereal variation of the speed of light over a period of 23 hours 56 minutes with an amplitude of about 8 km/s). [34]

Applying the Titius–Bode law to the Earth–Moon system, which he generalizes to aether, Allais calculates a "wind" of 7.95 km/s, which is comparable to the values found by the experiments of Michelson and Miller. Hence Allais deduces that the aether turns with the stars, as proposed by the aether drag hypothesis, and is not fixed as Hendrik Lorentz thought when inventing his famous transformation and his ether theory. But the majority of scientists at the end of the 19th century imagined that such an aether crossed the Earth so that the rotation of the Earth around the Sun would cause an important variation of 30 km/s. Consequently, since the third postulate on which special relativity is based is the constancy of the speed of light in a vacuum, Allais considers it unfounded. In order to measure a change in the speed of light, one would have to get back to the definition of the 1960 meter, since confidence in the theory of relativity nowadays is such that current metrology uses constancy of the speed of light as an axiom.

Allais summarized his experimental work in English in his 1999 memoir on behalf of NASA. [5] He detailed his aether hypothesis in the books L'Anisotropie de l'Espace, published in 1997, [30] and L'Effondrement de la Théorie de la Relativité, published in 2004. [35] A book on Allais' scientific legacy has been edited in English in 2011, [36] yet his aether hypothesis has not gained significant traction among mainstream scientists. Nevertheless, after Allais' death in 2010, experiments on the Allais effect continue. [37]

See also

Related Research Articles

<span class="mw-page-title-main">Gravitational constant</span> Physical constant relating the gravitational force between objects to their mass and distance

The gravitational constant, denoted by the capital letter G, is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's theory of general relativity.

The following is a timeline of gravitational physics and general relativity.

In physics, there are four observed fundamental interactions that form the basis of all known interactions in nature: gravitational, electromagnetic, strong nuclear, and weak nuclear forces. Some speculative theories have proposed a fifth force to explain various anomalous observations that do not fit existing theories. The characteristics of this fifth force depend on the hypothesis being advanced. Many postulate a force roughly the strength of gravity with a range of anywhere from less than a millimeter to cosmological scales. Another proposal is a new weak force mediated by W′ and Z′ bosons.

<span class="mw-page-title-main">Maurice Allais</span> French economist (1911–2010)

Maurice Félix Charles Allais was a French physicist and economist, the 1988 winner of the Nobel Memorial Prize in Economic Sciences "for his pioneering contributions to the theory of markets and efficient utilization of resources", along with John Hicks and Paul Samuelson, to neoclassical synthesis. They formalize the self-regulation of markets, which Keynes refuted but reiterated some of Allais's ideas.

<span class="mw-page-title-main">Equivalence principle</span> The hypothesis that inertial and gravitational masses are equivalent

The equivalence principle is the hypothesis that the observed equivalence of gravitational and inertial mass is a consequence of nature. The weak form, known for centuries, relates to masses of any composition in free fall taking the same trajectories and landing at identical times. The extended form by Albert Einstein requires special relativity to also hold in free fall and requires the weak equivalence to be valid everywhere. This form was a critical input for the development of the theory of general relativity. The strong form requires Einstein's form to work for stellar objects. Highly precise experimental tests of the principle limit possible deviations from equivalence to be very small.

The Pioneer anomaly, or Pioneer effect, was the observed deviation from predicted accelerations of the Pioneer 10 and Pioneer 11 spacecraft after they passed about 20 astronomical units (3×109 km; 2×109 mi) on their trajectories out of the Solar System. The apparent anomaly was a matter of much interest for many years but has been subsequently explained by anisotropic radiation pressure caused by the spacecraft's heat loss.

<span class="mw-page-title-main">Gravimetry</span> Measurement of the strength of a gravitational field

Gravimetry is the measurement of the strength of a gravitational field. Gravimetry may be used when either the magnitude of a gravitational field or the properties of matter responsible for its creation are of interest. The study of gravity changes belongs to geodynamics.

In the 19th century, the theory of the luminiferous aether as the hypothetical medium for the propagation of light waves was widely discussed. The aether hypothesis arose because physicists of that era could not conceive of light waves propagating without a physical medium in which to do so. When experiments failed to detect the hypothesized luminiferous aether, physicists conceived explanations for the experiments' failure which preserved the hypothetical aether's existence.

Tests of general relativity serve to establish observational evidence for the theory of general relativity. The first three tests, proposed by Albert Einstein in 1915, concerned the "anomalous" precession of the perihelion of Mercury, the bending of light in gravitational fields, and the gravitational redshift. The precession of Mercury was already known; experiments showing light bending in accordance with the predictions of general relativity were performed in 1919, with increasingly precise measurements made in subsequent tests; and scientists claimed to have measured the gravitational redshift in 1925, although measurements sensitive enough to actually confirm the theory were not made until 1954. A more accurate program starting in 1959 tested general relativity in the weak gravitational field limit, severely limiting possible deviations from the theory.

General relativity is a theory of gravitation that was developed by Albert Einstein between 1907 and 1915, with contributions by many others after 1915. According to general relativity, the observed gravitational attraction between masses results from the warping of space and time by those masses.

In theoretical astrophysics, the Nordtvedt effect refers to the relative motion between the Earth and the Moon that would be observed if the gravitational self-energy of a body contributed differently to its gravitational mass than to its inertial mass. If observed, the Nordtvedt effect would violate the strong equivalence principle, which indicates that an object's movement in a gravitational field does not depend on its mass or composition. No evidence of the effect has been found.

The term gravitational shielding refers to a hypothetical process of shielding an object from the influence of a gravitational field. Such processes, if they existed, would have the effect of reducing the weight of an object. The shape of the shielded region would be similar to a shadow from the gravitational shield. For example, the shape of the shielded region above a disk would be conical. The height of the cone's apex above the disk would vary directly with the height of the shielding disk above the Earth. Experimental evidence to date indicates that no such effect exists. Gravitational shielding is considered to be a violation of the equivalence principle and therefore inconsistent with both Newtonian theory and general relativity.

The flyby anomaly is a discrepancy between current scientific models and the actual increase in speed observed during a planetary flyby by a spacecraft. In multiple cases, spacecraft have been observed to gain greater speed than scientists had predicted, but thus far no convincing explanation has been found. This anomaly has been observed as shifts in the S-band and X-band Doppler and ranging telemetry. The largest discrepancy noticed during a flyby has been 13.46 mm/s.

<span class="mw-page-title-main">Paraconical pendulum</span>

The paraconical pendulum is a type of pendulum invented in the 1950s by Maurice Allais, a French researcher. During the 1950s, Maurice Allais conducted six marathon series of long-term observations, during each of which his team manually operated and manually monitored his pendulum non-stop over about a month. The objective was to investigate possible changes over time of the characteristics of the motion, hypothesized to yield information about asymmetries of inertial space.

The Eötvös experiment was a famous physics experiment that measured the correlation between inertial mass and gravitational mass, demonstrating that the two were one and the same, something that had long been suspected but never demonstrated with the same accuracy. The earliest experiments were done by Isaac Newton (1642–1727) and improved upon by Friedrich Wilhelm Bessel (1784–1846). A much more accurate experiment using a torsion balance was carried out by Loránd Eötvös starting around 1885, with further improvements in a lengthy run between 1906 and 1909. Eötvös's team followed this with a series of similar but more accurate experiments, as well as experiments with different types of materials and in different locations around the Earth, all of which demonstrated the same equivalence in mass. In turn, these experiments led to the modern understanding of the equivalence principle encoded in general relativity, which states that the gravitational and inertial masses are the same.

Erwin Joseph Saxl was a physicist and inventor. He was born in Vienna in 1904 and received his Ph.D. there in 1927. In the late 1920s he emigrated to the United States. In 1935 he founded the Saxl Instrument Company, which designed and manufactured tension meters for use in the textile industry, and later in other industries. The company, which Saxl ran jointly with his wife, Lucretia Hildreth Saxl, from their home in Harvard, Massachusetts, was renamed Tensitron in 1953. Saxl is reported as having stated that he worked under Albert Einstein. He died in 1981.

<span class="mw-page-title-main">Mildred Allen (physicist)</span> American physicist

Mildred Allen was an American physicist.

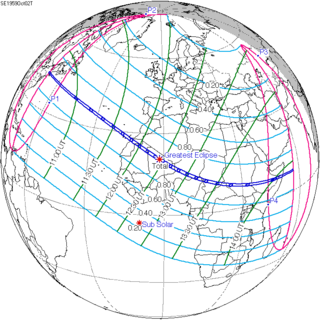
<span class="mw-page-title-main">Solar eclipse of October 2, 1959</span> Total eclipse

A total solar eclipse occurred on October 2, 1959. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. A total solar eclipse occurs when the Moon's apparent diameter is larger than the Sun's, blocking all direct sunlight, turning day into darkness. Totality occurs in a narrow path across Earth's surface, with the partial solar eclipse visible over a surrounding region thousands of kilometres wide. Totality was visible from northeastern Massachusetts and the southern tip of New Hampshire in the United States, Canary Islands, Morocco, Spanish Sahara including the capital city Laayoune, French Mauritania, Mali Federation, French Niger, British Nigeria, British Cameroons and French Cameroons, French Chad including the capital city Fort-Lamy, French Central Africa, Sudan, Ethiopia, and the Trust Territory of Somaliland.

Jens Horst Gundlach is a German physicist.

<span class="mw-page-title-main">Lunar Surface Gravimeter</span> 1972 Apollo lunar science experiment

The Lunar Surface Gravimeter (LSG) was a lunar science experiment that was deployed on the surface of the Moon by the astronauts of Apollo 17 on December 12, 1972. The LSG was conceived by its principal investigator Joseph Weber. Weber proposed a number of experimental methods for the detection of gravitational waves, and would go on to be described as the "founding father" of gravitational wave detection. The experiment aimed to measure changes in the local gravitational strength on the Moon's surface through the use of a gravimeter. These measurements were intended to provide insight into the internal structures of the Moon as it tidally deformed due interaction with the gravitational fields of the Earth and Sun. In addition the experiment hoped to contribute experimental evidence of the existence of gravitational waves.

References

  1. ↑ Hecht, Laurence (24 October 2010). "In Appreciation of Maurice Allais (1911-2010) The New Physical Field of Maurice Allais" (PDF). 21st Century Science & Technology. pp. 26–30.
  2. ↑ Allais, M. (September 1959). "Should the Laws of Gravitation Be reconsidered? Part I – Abnormalities in the Motion of a Paraconical Pendulum on an Anisotropic Support" (PDF). Aero/Space Engineering: 46–52. Archived from the original (PDF) on 2015-07-20.
  3. ↑ Allais, M. (October 1959). "Should the Laws of Gravitation Be reconsidered? Part II – Experiments in Connection with the Abnormalities Noted in the Motion of the Paraconical Pendulum With an Anisotropic Support" (PDF). Aero/Space Engineering: 51–55. Archived from the original (PDF) on 2016-06-22.
  4. ↑ Allais, Maurice (1959). New theoretical and experimental research work on gravity. Memoir (Report).
  5. 1 2 3 4 Allais, Maurice (November 1999). The 'Allais Effect' and my experiments with the paraconical pendulum (1954-1960) (PDF). Memoir C-6083 prepared for NASA (Report).
  6. ↑ Jeverdan, G. T.; Rusu, G. I.; Antonescu, V. I. (15 February 1961). "Date preliminare asupra comportarii unui pendul Foucault in timpul eclipsei de soare de la 15 februarie 1961" [Preliminary data about the behavior of a Foucault pendulum during the Sun eclipse of 15 February 15, 1961]. Annals of the Alexandru Ioan Cuza University (in Romanian). 7 (2): 457.
  7. ↑ Jeverdan, G. T.; Rusu, G. I.; Antonescu, V. I. (1981). "Experiments using the Foucault pendulum during the solar eclipse of 15 February, 1961" (PDF). The Biblical Astronomer. 1 (55): 18–20. Archived from the original (PDF) on 2008-08-27. Retrieved 2017-03-28.
  8. ↑ Saxl, Erwin J.; Allen, Mildred (15 February 1971). "1970 Solar Eclipse as 'Seen' by a Torsion Pendulum" (PDF). Physical Review D. 3 (4): 823–825. Bibcode:1971PhRvD...3..823S. doi:10.1103/PhysRevD.3.823. Archived from the original (PDF) on 2017-05-19. Retrieved 2017-03-27.
  9. ↑ Savrov, L. A.; Yushkin, V. D. (January 1995). "Paraconical pendulum as a detector of gravitational effects during solar eclipses (processing data and results)" (PDF). Measurement Techniques. 38 (1). Springer Science+Business Media: 9–13. Bibcode:1995MeasT..38..253S. doi:10.1007/BF00976738. S2CID   120963357. Archived from the original (PDF) on 2017-03-29. Retrieved 2017-03-28.
  10. ↑ Savrov, L. A. (March 1995). "Paraconical pendulum as a detector of gravitational effects during solar eclipses (processing data and results)" (PDF). Measurement Techniques. 38 (3). Springer Science+Business Media: 253–260. Bibcode:1995MeasT..38..253S. doi:10.1007/BF00977602. S2CID   122031984. Archived from the original (PDF) on 2017-03-29. Retrieved 2017-03-28.
  11. ↑ Savrov, L. A. (April 2009). "Improved determination of variation of rate of rotation of oscillation plane of a paraconic pendulum during the solar eclipse in Mexico on July 11, 1991". Measurement Techniques. 52 (4). Springer Science+Business Media: 339–343. doi:10.1007/s11018-009-9291-6. S2CID   122985875.
  12. ↑ Savrov, L. A. (June 1997). "Experiment with paraconic pendulums during the November 3, 1994 solar eclipse in Brazil". Measurement Techniques. 40 (6). Springer Science+Business Media: 511–516. Bibcode:1997MeasT..40..511S. doi:10.1007/BF02504372. S2CID   120976498.
  13. ↑ Zhou, S. W.; Huang, B. J.; Ren, Z. M. (1995). "The abnormal influence of the partial solar eclipse on December 24th, 1992, on the time comparisons between atomic clocks". Il Nuovo Cimento C. 18 (2): 223–236. Bibcode:1995NCimC..18..223Z. doi:10.1007/BF02512022. S2CID   123012966.
  14. ↑ Mishra, D. C.; Rao, M. B. S. Vyaghreswara (1997). "Temporal variation in gravity field during solar eclipse on 24 October 1995". Current Science. 72 (11): 782–783.
  15. ↑ Wang, Q.S.; Yang, X.S.; Wu, C.Z.; Guo, G.H.; Liu, H.C.; Hua, C.C. (14 July 2000). "Precise measurement of gravity variations during a total solar eclipse" (PDF). Physical Review D. 62 (4): 041101. arXiv: 1003.4947 . Bibcode:2000PhRvD..62d1101W. doi:10.1103/PhysRevD.62.041101. S2CID   6846335.
  16. ↑ Popescu, V. A.; Olenici, D. (August 2007). A confirmation of the Allais and Jeverdan-Rusu-Antonescu effects during the solar eclipse from 22 September 2006, and the quantization of behaviour of pendulum (PDF). 7th Biennial European SSE Meeting. Røros, Norway: Society for Scientific Exploration.
  17. ↑ Goodey, T. J.; Pugach, A. F.; Olenici, D. (2010). "Correlated anomalous effects observed during a solar eclipse". Journal of Advanced Research in Physics. 1 (2). Archived from the original on 2017-03-29. Retrieved 2017-03-28.
  18. ↑ Pugach, A. F.; Olenici, D. (2012). "Observations of Correlated Behavior of Two Light Torsion Balances and a Paraconical Pendulum in Separate Locations during the Solar Eclipse of January 26th, 2009" (PDF). Advances in Astronomy. 2012: 263818. Bibcode:2012AdAst2012E...2P. doi: 10.1155/2012/263818 .
  19. ↑ Slichter, L. B.; Caputo, M.; Hager, C. L. (15 March 1965). "An experiment concerning gravitational shielding". Journal of Geophysical Research. 70 (6): 1541–1551. Bibcode:1965JGR....70.1541S. doi:10.1029/JZ070i006p01541.
  20. ↑ Kuusela, T. (15 March 1991). "Effect of the solar eclipse on the period of a torsion pendulum". Physical Review D. 43 (6): 2041–2043. Bibcode:1991PhRvD..43.2041K. doi:10.1103/PhysRevD.43.2041. PMID   10013582.
  21. ↑ Jun, Luo; Jianguo, Li; Xuerong, Zhang; Liakhovets, V.; Lomonosov, M.; Ragyn, A. (15 October 1991). "Observation of 1990 solar eclipse by a torsion pendulum". Physical Review D. 44 (8): 2611–2613. Bibcode:1991PhRvD..44.2611L. doi:10.1103/PhysRevD.44.2611. PMID   10014147.
  22. ↑ Leslie Mullen (1999). "Decrypting the Eclipse". Archived copy of NASA web page. Archived from the original on 2008-05-16.
  23. ↑ Dave Dooling (12 October 1999). "French Nobel Laureate turns back clock". NASA.
  24. ↑ Thomas Goodey (2000). "Information available about what happened in the NASA 1999 Eclipse Experiments". allais.wiki.
  25. ↑ Yang, Xin-She; Wang, Qian-Shen (October 2002). "Gravity Anomaly During the Mohe Total Solar Eclipse and New Constraint on Gravitational Shielding Parameter" (PDF). Astrophysics and Space Science. 282 (1): 245–253. Bibcode:2002Ap&SS.282..245Y. doi:10.1023/A:1021119023985. S2CID   118497439. Archived from the original (PDF) on 2012-01-12. Retrieved 2017-03-27.
  26. ↑ Van Flandern, T.; Yang, X. S. (15 January 2003). "Allais gravity and pendulum effects during solar eclipses explained" (PDF). Physical Review D. 67 (2): 022002. Bibcode:2003PhRvD..67b2002V. doi:10.1103/PhysRevD.67.022002.
  27. ↑ Phil McKenna (19 July 2009). "July eclipse is best chance to look for gravity anomaly". NewScientist.
  28. ↑ "Eclipse at Sheshan Hill". The Atlantic. July 2009.
  29. ↑ Salva, Horacio R. (15 March 2011). "Searching the Allais effect during the total sun eclipse of 11 July 2010". Physical Review D. 83 (6): 067302. Bibcode:2011PhRvD..83f7302S. doi:10.1103/PhysRevD.83.067302.
  30. 1 2 Allais, Maurice (1997). L'Anisotropie de l'Espace [The Anisotropy of Space](PDF) (in French). Clément Juglar Editions. ISBN   978-2908735093.
  31. ↑ Miller, Dayton C. (July 1933). "The Ether-Drift experiment and the determination of the absolute motion of the Earth" (PDF). Reviews of Modern Physics. 5 (3): 203–254. Bibcode:1933RvMP....5..203M. doi:10.1103/RevModPhys.5.203. S2CID   4119615.
  32. ↑ Allais, Maurice (1998). "The experiments of Dayton C. Miller (1925-1926) and the theory of relativity" (PDF). 21st Century Science & Technology. pp. 26–32.
  33. ↑ Shankland, R. S.; McCuskey, S. W..; Leone, F. C.; Kuerti, G. (April 1955). "New Analysis of the Interferometer Observations of Dayton C. Miller". Reviews of Modern Physics. 27 (2): 167–178. Bibcode:1955RvMP...27..167S. doi:10.1103/RevModPhys.27.167.
  34. ↑ Deloly, Jean-Bernard. "The re-examination of Miller's interferometric observations and of Esclangon's observations". Maurice Allais Foundation.
  35. ↑ Allais, Maurice (2004). L'Effondrement de la Théorie de la Relativité – Implication irréfragable des données de l'expérience[The Collapse of the Theory of Relativity – Irrefutable implication of the empirical data] (in French). Clément Juglar Editions. ISBN   978-2908735185.
  36. ↑ Múnera, Héctor A., ed. (May 2011). Should the Laws of Gravitation be Reconsidered?: The Scientific Legacy of Maurice Allais. Apeiron. ISBN   978-0986492655.
  37. ↑ Deloly, Jean-Bernard (22 April 2016). "Continuation given to Maurice Allais's experimental works. State of the situation (2015)" (PDF). Maurice Allais Foundation.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.