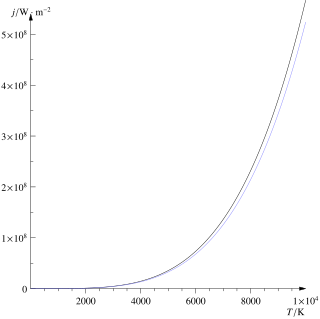
The Stefan–Boltzmann law, also known as Stefan's law, describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically.
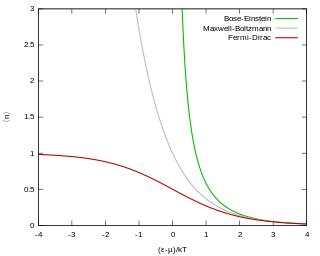
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics.

In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density is low enough to render quantum effects negligible.

A Fermi gas is an idealized model, an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi.

In quantum statistics, Bose–Einstein statistics describes one of two possible ways in which a collection of non-interacting identical particles may occupy a set of available discrete energy states at thermodynamic equilibrium. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose, who recognized that a collection of identical and indistinguishable particles can be distributed in this way. The idea was later adopted and extended by Albert Einstein in collaboration with Bose.

In physics, Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.

In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature (isothermal). The change in the Helmholtz energy during a process is equal to the maximum amount of work that the system can perform in a thermodynamic process in which temperature is held constant. At constant temperature, the Helmholtz free energy is minimized at equilibrium.

The internal energy of a thermodynamic system is the energy contained within it, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accounting for the gains and losses of energy due to changes in its internal state, including such quantities as magnetization. It excludes the kinetic energy of motion of the system as a whole and the potential energy of position of the system as a whole, with respect to its surroundings and external force fields. It includes the thermal energy, i.e., the constituent particles' kinetic energies of motion relative to the motion of the system as a whole. The internal energy of an isolated system cannot change, as expressed in the law of conservation of energy, a foundation of the first law of thermodynamics.

Certain systems can achieve negative thermodynamic temperature; that is, their temperature can be expressed as a negative quantity on the Kelvin or Rankine scales. This should be distinguished from temperatures expressed as negative numbers on non-thermodynamic Celsius or Fahrenheit scales, which are nevertheless higher than absolute zero. A system with a truly negative temperature on the Kelvin scale is hotter than any system with a positive temperature. If a negative-temperature system and a positive-temperature system come in contact, heat will flow from the negative- to the positive-temperature system. A standard example of such a system is population inversion in laser physics.

The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.

In classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in translational motion of a molecule should equal that in rotational motion.

The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials. Basically, Ohm's law was well established and stated that the current J and voltage V driving the current are related to the resistance R of the material. The inverse of the resistance is known as the conductance. When we consider a metal of unit length and unit cross sectional area, the conductance is known as the conductivity, which is the inverse of resistivity. The Drude model attempts to explain the resistivity of a conductor in terms of the scattering of electrons by the relatively immobile ions in the metal that act like obstructions to the flow of electrons.
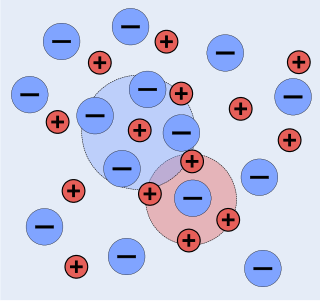
The chemists Peter Debye and Erich Hückel noticed that solutions that contain ionic solutes do not behave ideally even at very low concentrations. So, while the concentration of the solutes is fundamental to the calculation of the dynamics of a solution, they theorized that an extra factor that they termed gamma is necessary to the calculation of the activities of the solution. Hence they developed the Debye–Hückel equation and Debye–Hückel limiting law. The activity is only proportional to the concentration and is altered by a factor known as the activity coefficient . This factor takes into account the interaction energy of ions in solution.
Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed, stretched or generally deformed in any manner. Elasticity theory primarily develops formalisms for the mechanics of solid bodies and materials. The elastic potential energy equation is used in calculations of positions of mechanical equilibrium. The energy is potential as it will be converted into other forms of energy, such as kinetic energy and sound energy, when the object is allowed to return to its original shape (reformation) by its elasticity.
The Poisson–Boltzmann equation is a useful equation in many settings, whether it be to understand physiological interfaces, polymer science, electron interactions in a semiconductor, or more. It aims to describe the distribution of the electric potential in solution in the direction normal to a charged surface. This distribution is important to determine how the electrostatic interactions will affect the molecules in solution. The Poisson–Boltzmann equation is derived via mean-field assumptions. From the Poisson–Boltzmann equation many other equations have been derived with a number of different assumptions.

Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.

Anatoly Alexeyevich Karatsuba was a Russian mathematician working in the field of analytic number theory, p-adic numbers and Dirichlet series.

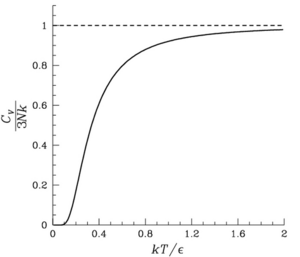
The Dulong–Petit law, a thermodynamic law proposed by French physicists Pierre Louis Dulong and Alexis Thérèse Petit, states that the classical expression for the molar specific heat capacity of certain chemical elements is constant for temperatures far from the absolute zero.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.
In solid state physics the electronic specific heat, sometimes called the electron heat capacity, is the specific heat of an electron gas. Heat is transported by phonons and by free electrons in solids. For pure metals, however, the electronic contributions dominate in the thermal conductivity. In impure metals, the electron mean free path is reduced by collisions with impurities, and the phonon contribution may be comparable with the electronic contribution.