In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
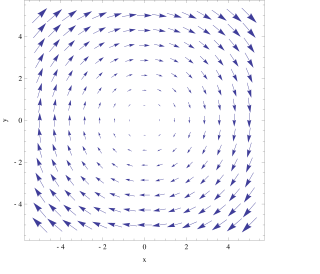
In vector calculus, the curl, also known as rotor, is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field.

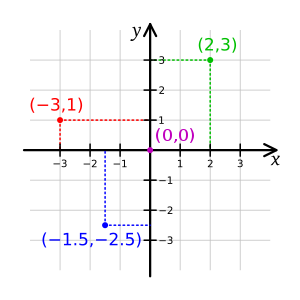
In geometry, a Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, called coordinate lines, coordinate axes or just axes of the system. The point where they meet is called the origin and has (0, 0) as coordinates.
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

In mathematics, a linear equation is an equation that may be put in the form where are the variables, and are the coefficients, which are often real numbers. The coefficients may be considered as parameters of the equation and may be arbitrary expressions, provided they do not contain any of the variables. To yield a meaningful equation, the coefficients are required to not all be zero.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three numbers, : the radial distance of the radial liner connecting the point to the fixed point of origin ; the polar angle θ of the radial line r; and the azimuthal angle φ of the radial line r.

In mathematics, physics, and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Euclidean vectors can be added and scaled to form a vector space. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by
Kinematics is a subfield of physics and mathematics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of both applied and pure mathematics since it can be studied without considering the mass of a body or the forces acting upon it. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.

In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcul, are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix. They are also used in fundamental elliptic curve cryptography algorithms.
In geometry, an incidence relation is a heterogeneous relation that captures the idea being expressed when phrases such as "a point lies on a line" or "a line is contained in a plane" are used. The most basic incidence relation is that between a point, P, and a line, l, sometimes denoted P I l. If P I l the pair (P, l) is called a flag. There are many expressions used in common language to describe incidence (for example, a line passes through a point, a point lies in a plane, etc.) but the term "incidence" is preferred because it does not have the additional connotations that these other terms have, and it can be used in a symmetric manner. Statements such as "line l1 intersects line l2" are also statements about incidence relations, but in this case, it is because this is a shorthand way of saying that "there exists a point P that is incident with both line l1 and line l2". When one type of object can be thought of as a set of the other type of object (viz., a plane is a set of points) then an incidence relation may be viewed as containment.

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in R3 passing through the origin. The real projective plane is then an extension of the (ordinary) plane — to every point (v1,v2) of the ordinary plane, the line spanned by (v1,v2,1) is associated (i.e., the real projective plane is the projective completion of the ordinary plane, cf. also the homogeneous coordinates below) while there are also some “points in the infinity”.
In projective geometry, duality or plane duality is a formalization of the striking symmetry of the roles played by points and lines in the definitions and theorems of projective planes. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.
In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogeneous coordinates to each line in projective 3-space, . Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines in and points on a quadric in . A predecessor and special case of Grassmann coordinates, Plücker coordinates arise naturally in geometric algebra. They have proved useful for computer graphics, and also can be extended to coordinates for the screws and wrenches in the theory of kinematics used for robot control.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.
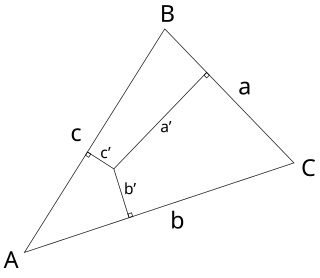
In geometry, the trilinear coordinatesx : y : z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x : y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y : z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z : x and vertices C and A.

In Euclidean geometry, the intersection of a line and a line can be the empty set, a point, or another line. Distinguishing these cases and finding the intersection have uses, for example, in computer graphics, motion planning, and collision detection.
In Euclidean space, the distance from a point to a plane is the distance between a given point and its orthogonal projection on the plane, the perpendicular distance to the nearest point on the plane.
In geometry, line coordinates are used to specify the position of a line just as point coordinates are used to specify the position of a point.