Grammatical evolution

Last updated

Grammatical evolution (GE) is an evolutionary computation and, more specifically, a genetic programming (GP) technique (or approach) pioneered by Conor Ryan, JJ Collins and Michael O'Neill in 1998 [1] at the BDS Group in the University of Limerick.

Contents

As in any other GP approach, the objective is to find an executable program, program fragment, or function, which will achieve a good fitness value for a given objective function. In most published work on GP, a LISP-style tree-structured expression is directly manipulated, whereas GE applies genetic operators to an integer string, subsequently mapped to a program (or similar) through the use of a grammar, which is typically expressed in Backus–Naur form. One of the benefits of GE is that this mapping simplifies the application of search to different programming languages and other structures.

Problem addressed

In type-free, conventional Koza-style GP, the function set must meet the requirement of closure: all functions must be capable of accepting as their arguments the output of all other functions in the function set. Usually, this is implemented by dealing with a single data-type such as double-precision floating point. While modern Genetic Programming frameworks support typing, such type-systems have limitations that Grammatical Evolution does not suffer from.

GE's solution

GE offers a solution to the single-type limitation by evolving solutions according to a user-specified grammar (usually a grammar in Backus-Naur form). Therefore the search space can be restricted, and domain knowledge of the problem can be incorporated. The inspiration for this approach comes from a desire to separate the "genotype" from the "phenotype": in GP, the objects the search algorithm operates on and what the fitness evaluation function interprets are one and the same. In contrast, GE's "genotypes" are ordered lists of integers which code for selecting rules from the provided context-free grammar. The phenotype, however, is the same as in Koza-style GP: a tree-like structure that is evaluated recursively. This model is more in line with how genetics work in nature, where there is a separation between an organism's genotype and the final expression of phenotype in proteins, etc.

Separating genotype and phenotype allows a modular approach. In particular, the search portion of the GE paradigm needn't be carried out by any one particular algorithm or method. Observe that the objects GE performs search on are the same as those used in genetic algorithms. This means, in principle, that any existing genetic algorithm package, such as the popular GAlib, can be used to carry out the search, and a developer implementing a GE system need only worry about carrying out the mapping from list of integers to program tree. It is also in principle possible to perform the search using some other method, such as particle swarm optimization (see the remark below); the modular nature of GE creates many opportunities for hybrids as the problem of interest to be solved dictates.

Brabazon and O'Neill have successfully applied GE to predicting corporate bankruptcy, forecasting stock indices, bond credit ratings, and other financial applications.[ citation needed ] GE has also been used with a classic predator-prey model to explore the impact of parameters such as predator efficiency, niche number, and random mutations on ecological stability. [2]

It is possible to structure a GE grammar that for a given function/terminal set is equivalent to genetic programming.

Criticism

Despite its successes, GE has been the subject of some criticism. One issue is that as a result of its mapping operation, GE's genetic operators do not achieve high locality [3] [4] which is a highly regarded property of genetic operators in evolutionary algorithms. [3]

Variants

Although GE was originally described in terms of using an Evolutionary Algorithm, specifically, a Genetic Algorithm, other variants exist. For example, GE researchers have experimented with using particle swarm optimization to carry out the searching instead of genetic algorithms with results comparable to that of normal GE; this is referred to as a "grammatical swarm"; using only the basic PSO model it has been found that PSO is probably equally capable of carrying out the search process in GE as simple genetic algorithms are. (Although PSO is normally a floating-point search paradigm, it can be discretized, e.g., by simply rounding each vector to the nearest integer, for use with GE.)

Yet another possible variation that has been experimented with in the literature is attempting to encode semantic information in the grammar in order to further bias the search process. Other work showed that, with biased grammars that leverage domain knowledge, even random search can be used to drive GE. [5]

GE was originally a combination of the linear representation as used by the Genetic Algorithm for Developing Software (GADS)[ citation needed ] and Backus Naur Form grammars, which were originally used in tree-based GP by Wong and Leung [6] in 1995 and Whigham in 1996. [7] Other related work noted in the original GE paper was that of Frederic Gruau, [8] who used a conceptually similar "embryonic" approach, as well as that of Keller and Banzhaf, [9] which similarly used linear genomes.

Implementations

There are several implementations of GE. These include the following.

Project nameLanguageYearLocation
GELabMatlab2018https://github.com/adilraja/GELAB
PonyGE2Python2017https://arxiv.org/abs/1703.08535
gramEvolR2016https://cran.r-project.org/web/packages/gramEvol/vignettes/ge-intro.pdf
PyNeurGenPython2012http://pyneurgen.sourceforge.net/
Grammatical_ evolutionRuby2011http://www.cleveralgorithms.com/nature-inspired/evolution/grammatical_evolution.rb
AGEC, Lua2011http://nohejl.name/age/pdf/AGE-Documentation-1.0.2.pdf
PonyGEPython2010https://code.google.com/archive/p/ponyge/downloads
GERETRuby2010https://github.com/bver/GERET/
GEVAJava2008http://ncra.ucd.ie/Site/GEVA.html
ECJJava2008https://cs.gmu.edu/~eclab/projects/ecj/
GENNC++2007https://ritchielab.org/research/past-research/52-grammatical-evolution-neural-networks
libGEC++, S-Lang, tinycc2004http://bds.ul.ie/libGE/

See also

Notes

  1. ↑ "Grammatical Evolution: Evolving Programs for an Arbitrary Language".
  2. ↑ Alfonseca, Manuel; Soler Gil, Francisco José (2 January 2015). "Evolving a predator-prey ecosystem of mathematical expressions with grammatical evolution". Complexity. 20 (3): 66–83. Bibcode:2015Cmplx..20c..66A. doi:10.1002/cplx.21507. hdl: 10486/663611 .
  3. 1 2 DOI.org
  4. ↑ "Publication: Positional Effect of Crossover and Mutation in Grammatical Evolution - School of Computing - University of Kent".
  5. ↑ O’Sullivan, John; Ryan, Conor (2002), Foster, James A.; Lutton, Evelyne; Miller, Julian; Ryan, Conor (eds.), "An Investigation into the Use of Different Search Strategies with Grammatical Evolution", Genetic Programming, Berlin, Heidelberg: Springer Berlin Heidelberg, vol. 2278, pp. 268–277, doi:10.1007/3-540-45984-7_26, ISBN   978-3-540-43378-1 , retrieved 2022-08-08
  6. ↑ Wong, Man Leung; Leung, Kwong Sak (November 1995). "Applying logic grammars to induce sub-functions in genetic programming". Proceedings of 1995 IEEE International Conference on Evolutionary Computation. Vol. 2. pp. 737–740 vol.2. doi:10.1109/ICEC.1995.487477. ISBN   0-7803-2759-4. S2CID   16071918.
  7. ↑ Whigham, P. (1996). "Search Bias, Language Bias and Genetic ProgrammingP". S2CID   16631215.{{cite web}}: Missing or empty |url= (help)
  8. ↑ Gruau, Frédéric (1994), Neural Network Synthesis Using Cellular Encoding And The Genetic Algorithm, CiteSeerX   10.1.1.29.5939
  9. ↑ Kellere, Robert E. (1996). "Genetic Programming Using Mutation, Reproduction and Genotype-phenotype Mapping from Linear Binary Genomes into Linear Lalr(1) Phenotypes Paper Category: Genetic Programming (gp)". S2CID   18095204.{{cite web}}: Missing or empty |url= (help)

Resources

Related Research Articles

In artificial intelligence, genetic programming (GP) is a technique of evolving programs, starting from a population of unfit programs, fit for a particular task by applying operations analogous to natural genetic processes to the population of programs.

<span class="mw-page-title-main">Genetic algorithm</span> Competitive algorithm for searching a problem space

In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on biologically inspired operators such as mutation, crossover and selection. Some examples of GA applications include optimizing decision trees for better performance, solving sudoku puzzles, hyperparameter optimization, causal inference, etc.

In computational intelligence (CI), an evolutionary algorithm (EA) is a subset of evolutionary computation, a generic population-based metaheuristic optimization algorithm. An EA uses mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions. Evolution of the population then takes place after the repeated application of the above operators.

In computer science, evolutionary computation is a family of algorithms for global optimization inspired by biological evolution, and the subfield of artificial intelligence and soft computing studying these algorithms. In technical terms, they are a family of population-based trial and error problem solvers with a metaheuristic or stochastic optimization character.

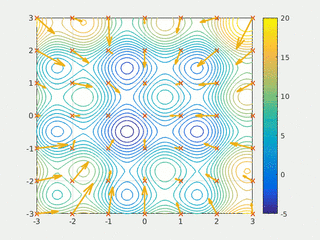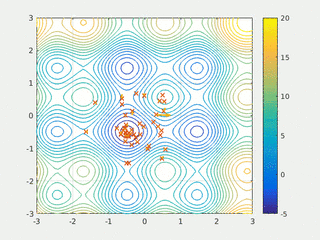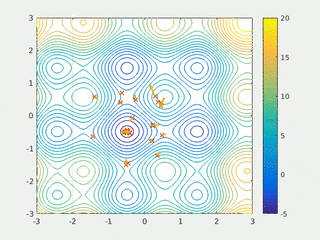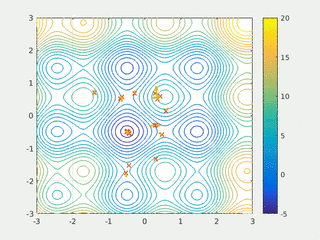
<span class="mw-page-title-main">Particle swarm optimization</span> Iterative simulation method

In computational science, particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formula over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.

Neuroevolution, or neuro-evolution, is a form of artificial intelligence that uses evolutionary algorithms to generate artificial neural networks (ANN), parameters, and rules. It is most commonly applied in artificial life, general game playing and evolutionary robotics. The main benefit is that neuroevolution can be applied more widely than supervised learning algorithms, which require a syllabus of correct input-output pairs. In contrast, neuroevolution requires only a measure of a network's performance at a task. For example, the outcome of a game can be easily measured without providing labeled examples of desired strategies. Neuroevolution is commonly used as part of the reinforcement learning paradigm, and it can be contrasted with conventional deep learning techniques that use backpropagation with a fixed topology.

In genetic algorithms (GA), or more general, evolutionary algorithms (EA), a chromosome is a set of parameters which define a proposed solution of the problem that the evolutionary algorithm is trying to solve. The set of all solutions, also called individuals according to the biological model, is known as the population. The genome of an individual consists of one, more rarely of several, chromosomes and corresponds to the genetic representation of the task to be solved. A chromosome is composed of a set of genes, where a gene consists of one or more semantically connected parameters, which are often also called decision variables. They determine one or more phenotypic characteristics of the individual or at least have an influence on them. In the basic form of genetic algorithms, the chromosome is represented as a binary string, while in later variants and in EAs in general, a wide variety of other data structures are used.

In computer science and mathematical optimization, a metaheuristic is a higher-level procedure or heuristic designed to find, generate, tune, or select a heuristic that may provide a sufficiently good solution to an optimization problem or a machine learning problem, especially with incomplete or imperfect information or limited computation capacity. Metaheuristics sample a subset of solutions which is otherwise too large to be completely enumerated or otherwise explored. Metaheuristics may make relatively few assumptions about the optimization problem being solved and so may be usable for a variety of problems.

In computer programming, gene expression programming (GEP) is an evolutionary algorithm that creates computer programs or models. These computer programs are complex tree structures that learn and adapt by changing their sizes, shapes, and composition, much like a living organism. And like living organisms, the computer programs of GEP are also encoded in simple linear chromosomes of fixed length. Thus, GEP is a genotype–phenotype system, benefiting from a simple genome to keep and transmit the genetic information and a complex phenotype to explore the environment and adapt to it.

Linear genetic programming (LGP) is a particular method of genetic programming wherein computer programs in a population are represented as a sequence of instructions from an imperative programming language or machine language. The adjective "linear" stems from the fact that the sequence of instructions is normally executed in a linear fashion. Like in other programs, the data flow in LGP can be modeled as a graph that will visualize the potential multiple usage of register contents and the existence of structurally noneffective code (introns) which are two main differences of this genetic representation from the more common tree-based genetic programming (TGP) variant.

In natural evolution and artificial evolution the fitness of a schema is rescaled to give its effective fitness which takes into account crossover and mutation.

In computer science and operations research, Genetic fuzzy systems are fuzzy systems constructed by using genetic algorithms or genetic programming, which mimic the process of natural evolution, to identify its structure and parameter.

<span class="mw-page-title-main">Syntax (programming languages)</span> Set of rules defining correctly structured programs

In computer science, the syntax of a computer language is the rules that define the combinations of symbols that are considered to be correctly structured statements or expressions in that language. This applies both to programming languages, where the document represents source code, and to markup languages, where the document represents data.

In computer programming, genetic representation is a way of presenting solutions/individuals in evolutionary computation methods. The term encompasses both the concrete data structures and data types used to realize the genetic material of the candidate solutions in the form of a genome, and the relationships between search space and problem space. In the simplest case, the search space corresponds to the problem space. The choice of problem representation is tied to the choice of genetic operators, both of which have a decisive effect on the efficiency of the optimization. Genetic representation can encode appearance, behavior, physical qualities of individuals. Difference in genetic representations is one of the major criteria drawing a line between known classes of evolutionary computation.

ECJ is a freeware evolutionary computation research system written in Java. It is a framework that supports a variety of evolutionary computation techniques, such as genetic algorithms, genetic programming, evolution strategies, coevolution, particle swarm optimization, and differential evolution. The framework models iterative evolutionary processes using a series of pipelines arranged to connect one or more subpopulations of individuals with selection, breeding (such as crossover, and mutation operators that produce new individuals. The framework is open source and is distributed under the Academic Free License. ECJ was created by Sean Luke, a computer science professor at George Mason University, and is maintained by Sean Luke and a variety of contributors.

GeneNetwork is a combined database and open-source bioinformatics data analysis software resource for systems genetics. This resource is used to study gene regulatory networks that link DNA sequence differences to corresponding differences in gene and protein expression and to variation in traits such as health and disease risk. Data sets in GeneNetwork are typically made up of large collections of genotypes and phenotypes from groups of individuals, including humans, strains of mice and rats, and organisms as diverse as Drosophila melanogaster, Arabidopsis thaliana, and barley. The inclusion of genotypes makes it practical to carry out web-based gene mapping to discover those regions of genomes that contribute to differences among individuals in mRNA, protein, and metabolite levels, as well as differences in cell function, anatomy, physiology, and behavior.

The MOEA Framework is an open-source evolutionary computation library for Java that specializes in multi-objective optimization. It supports a variety of multiobjective evolutionary algorithms (MOEAs), including genetic algorithms, genetic programming, grammatical evolution, differential evolution, and particle swarm optimization. As a result, it has been used to conduct numerous comparative studies to assess the efficiency, reliability, and controllability of state-of-the-art MOEAs.

Multi Expression Programming (MEP) is an evolutionary algorithm for generating mathematical functions describing a given set of data. MEP is a Genetic Programming variant encoding multiple solutions in the same chromosome. MEP representation is not specific. In the simplest variant, MEP chromosomes are linear strings of instructions. This representation was inspired by Three-address code. MEP strength consists in the ability to encode multiple solutions, of a problem, in the same chromosome. In this way, one can explore larger zones of the search space. For most of the problems this advantage comes with no running-time penalty compared with genetic programming variants encoding a single solution in a chromosome.

The following outline is provided as an overview of and topical guide to machine learning:

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.