Graph dynamical system

Last updated March 30, 2023

In mathematics, the concept of graph dynamical systems can be used to capture a wide range of processes taking place on graphs or networks. A major theme in the mathematical and computational analysis of GDSs is to relate their structural properties (e.g. the network connectivity) and the global dynamics that result.

The work on GDSs considers finite graphs and finite state spaces. As such, the research typically involves techniques from, e.g., graph theory, combinatorics, algebra, and dynamical systems rather than differential geometry. In principle, one could define and study GDSs over an infinite graph (e.g. cellular automata or probabilistic cellular automata over $\mathbb {Z} ^{k}$ or interacting particle systems when some randomness is included), as well as GDSs with infinite state space (e.g. $\mathbb {R}$ as in coupled map lattices); see, for example, Wu.^[1] In the following, everything is implicitly assumed to be finite unless stated otherwise.

Formal definition

A graph dynamical system is constructed from the following components:

A finite graphY with vertex set v[Y] = {1,2, ... , n}. Depending on the context the graph can be directed or undirected.
A state x_v for each vertex v of Y taken from a finite set K. The system state is the n-tuple x = (x₁, x₂, ... , x_n), and x[v] is the tuple consisting of the states associated to the vertices in the 1-neighborhood of v in Y (in some fixed order).
A vertex functionf_v for each vertex v. The vertex function maps the state of vertex v at time t to the vertex state at time t + 1 based on the states associated to the 1-neighborhood of v in Y.
An update scheme specifying the mechanism by which the mapping of individual vertex states is carried out so as to induce a discrete dynamical system with map F: Kⁿ → Kⁿ.

The phase space associated to a dynamical system with map F: Kⁿ → Kⁿ is the finite directed graph with vertex set Kⁿ and directed edges (x, F(x)). The structure of the phase space is governed by the properties of the graph Y, the vertex functions (f_i)_i, and the update scheme. The research in this area seeks to infer phase space properties based on the structure of the system constituents. The analysis has a local-to-global character.

Generalized cellular automata (GCA)

If, for example, the update scheme consists of applying the vertex functions synchronously one obtains the class of generalized cellular automata (CA). In this case, the global map F: Kⁿ → Kⁿ is given by

$F(x)_{v}=f_{v}(x[v])\;.$

This class is referred to as generalized cellular automata since the classical or standard cellular automata are typically defined and studied over regular graphs or grids, and the vertex functions are typically assumed to be identical.

Example: Let Y be the circle graph on vertices {1,2,3,4} with edges {1,2}, {2,3}, {3,4} and {1,4}, denoted Circ₄. Let K = {0,1} be the state space for each vertex and use the function nor₃ : K³ → K defined by nor₃(x,y,z) = (1 + x)(1 + y)(1 + z) with arithmetic modulo 2 for all vertex functions. Then for example the system state (0,1,0,0) is mapped to (0, 0, 0, 1) using a synchronous update. All the transitions are shown in the phase space below.

Sequential dynamical systems (SDS)

If the vertex functions are applied asynchronously in the sequence specified by a word w = (w₁, w₂, ... , w_m) or permutation $\pi$ = ( $\pi _{1}$ , $\pi _{2},\dots ,\pi _{n}$ ) of v[Y] one obtains the class of Sequential dynamical systems (SDS).^[2] In this case it is convenient to introduce the Y-local maps F_i constructed from the vertex functions by

F_{i}(x)=(x_{1},x_{2},\ldots ,x_{i-1},f_{i}(x[i]),x_{i+1},\ldots ,x_{n})\;.

The SDS map F = [F_Y , w] : Kⁿ → Kⁿ is the function composition

[F_{Y},w]=F_{w(m)}\circ F_{w(m-1)}\circ \cdots \circ F_{w(2)}\circ F_{w(1)}\;.

If the update sequence is a permutation one frequently speaks of a permutation SDS to emphasize this point.

Example: Let Y be the circle graph on vertices {1,2,3,4} with edges {1,2}, {2,3}, {3,4} and {1,4}, denoted Circ₄. Let K={0,1} be the state space for each vertex and use the function nor₃ : K³ → K defined by nor₃(x, y, z) = (1 + x)(1 + y)(1 + z) with arithmetic modulo 2 for all vertex functions. Using the update sequence (1,2,3,4) then the system state (0, 1, 0, 0) is mapped to (0, 0, 1, 0). All the system state transitions for this sequential dynamical system are shown in the phase space below.

Stochastic graph dynamical systems

From, e.g., the point of view of applications it is interesting to consider the case where one or more of the components of a GDS contains stochastic elements. Motivating applications could include processes that are not fully understood (e.g. dynamics within a cell) and where certain aspects for all practical purposes seem to behave according to some probability distribution. There are also applications governed by deterministic principles whose description is so complex or unwieldy that it makes sense to consider probabilistic approximations.

Every element of a graph dynamical system can be made stochastic in several ways. For example, in a sequential dynamical system the update sequence can be made stochastic. At each iteration step one may choose the update sequence w at random from a given distribution of update sequences with corresponding probabilities. The matching probability space of update sequences induces a probability space of SDS maps. A natural object to study in this regard is the Markov chain on state space induced by this collection of SDS maps. This case is referred to as update sequence stochastic GDS and is motivated by, e.g., processes where "events" occur at random according to certain rates (e.g. chemical reactions), synchronization in parallel computation/discrete event simulations, and in computational paradigms described later.

This specific example with stochastic update sequence illustrates two general facts for such systems: when passing to a stochastic graph dynamical system one is generally led to (1) a study of Markov chains (with specific structure governed by the constituents of the GDS), and (2) the resulting Markov chains tend to be large having an exponential number of states. A central goal in the study of stochastic GDS is to be able to derive reduced models.

One may also consider the case where the vertex functions are stochastic, i.e., function stochastic GDS. For example, Random Boolean networks are examples of function stochastic GDS using a synchronous update scheme and where the state space is K = {0, 1}. Finite probabilistic cellular automata (PCA) is another example of function stochastic GDS. In principle the class of Interacting particle systems (IPS) covers finite and infinite PCA, but in practice the work on IPS is largely concerned with the infinite case since this allows one to introduce more interesting topologies on state space.

Applications

Graph dynamical systems constitute a natural framework for capturing distributed systems such as biological networks and epidemics over social networks, many of which are frequently referred to as complex systems.

Related Research Articles

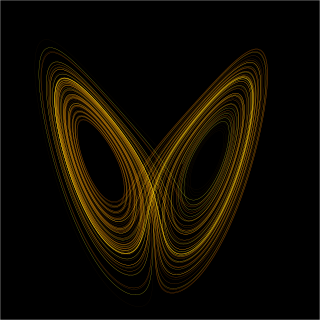
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.

In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variablesX_i are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin. Every variable X_i in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes ; this generalization is known as the Bernoulli scheme.

In mathematics, a function from a set $X$ to a set $Y$ assigns to each element of $X$ exactly one element of $Y$ . The set $X$ is called the domain of the function and the set $Y$ is called the codomain of the function.

In mathematics, Hall's marriage theorem, proved by Philip Hall (1935), is a theorem with two equivalent formulations:

In graph theory, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation $V$ of a quiver assigns a vector space $V (x)$ to each vertex $x$ of the quiver and a linear map $V (a)$ to each arrow $a$ .

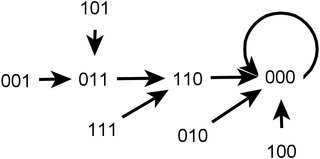
In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.

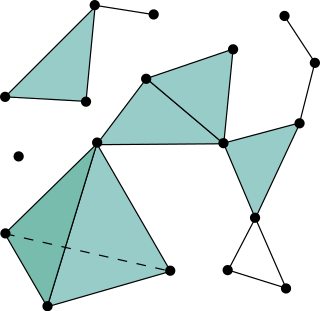
In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.

A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines relations between sets of strings.

In mathematics, a Markov decision process (MDP) is a discrete-time stochastic control process. It provides a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying optimization problems solved via dynamic programming. MDPs were known at least as early as the 1950s; a core body of research on Markov decision processes resulted from Ronald Howard's 1960 book, Dynamic Programming and Markov Processes. They are used in many disciplines, including robotics, automatic control, economics and manufacturing. The name of MDPs comes from the Russian mathematician Andrey Markov as they are an extension of Markov chains.

A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs have many applications throughout pure mathematics and are used to model various behaviours of stochastic models such as stock prices, random growth models or physical systems that are subjected to thermal fluctuations.

In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine. The most widely studied shift spaces are the subshifts of finite type.

In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity.

In mathematics, two functions are said to be topologically conjugate if there exists a homeomorphism that will conjugate the one into the other. Topological conjugacy, and related-but-distinct § Topological equivalence of flows, are important in the study of iterated functions and more generally dynamical systems, since, if the dynamics of one iterative function can be determined, then that for a topologically conjugate function follows trivially.

In topology, a branch of mathematics, the ends of a topological space are, roughly speaking, the connected components of the "ideal boundary" of the space. That is, each end represents a topologically distinct way to move to infinity within the space. Adding a point at each end yields a compactification of the original space, known as the end compactification.

In the mathematical field of dynamical systems, a random dynamical system is a dynamical system in which the equations of motion have an element of randomness to them. Random dynamical systems are characterized by a state space S, a set of maps $from S into itself that can be thought of as the set of all possible equations of motion, and a probability distribution Q on the set that represents the random choice of map. Motion in a random dynamical system can be informally thought of as a state evolving according to a succession of maps randomly chosen according to the distribution Q .$

<span class="mw-page-title-main">Sequential dynamical system</span> Class of graph dynamical systems

Sequential dynamical systems (SDSs) are a class of graph dynamical systems. They are discrete dynamical systems which generalize many aspects of for example classical cellular automata, and they provide a framework for studying asynchronous processes over graphs. The analysis of SDSs uses techniques from combinatorics, abstract algebra, graph theory, dynamical systems and probability theory.

<span class="mw-page-title-main">Abelian sandpile model</span> Cellular automaton

The Abelian sandpile model (ASM) is the more popular name of the original Bak–Tang–Wiesenfeld model (BTW). BTW model was the first discovered example of a dynamical system displaying self-organized criticality. It was introduced by Per Bak, Chao Tang and Kurt Wiesenfeld in a 1987 paper.

In the mathematics of infinite graphs, an end of a graph represents, intuitively, a direction in which the graph extends to infinity. Ends may be formalized mathematically as equivalence classes of infinite paths, as havens describing strategies for pursuit–evasion games on the graph, or as topological ends of topological spaces associated with the graph.

Stochastic cellular automata or probabilistic cellular automata (PCA) or random cellular automata or locally interacting Markov chains are an important extension of cellular automaton. Cellular automata are a discrete-time dynamical system of interacting entities, whose state is discrete.

In mathematics, a Markov odometer is a certain type of topological dynamical system. It plays a fundamental role in ergodic theory and especially in orbit theory of dynamical systems, since a theorem of H. Dye asserts that every ergodic nonsingular transformation is orbit-equivalent to a Markov odometer.

References

↑ Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007. S2CID 122111995.
↑ Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4.

External links

Graph Dynamical Systems – A Mathematical Framework for Interaction-Based Systems, Their Analysis and Simulations by Henning Mortveit

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[wu-05-1] Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007. S2CID 122111995.

[Mortveit-08-2] Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4.

[1]

[2]