
The travelling salesman problem, also known as the travelling salesperson problem (TSP), asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.
The nearest neighbor algorithm was one of the first algorithms used to solve the travelling salesman problem approximately. In that problem, the salesman starts at a random city and repeatedly visits the nearest city until all have been visited. The algorithm quickly yields a short tour, but usually not the optimal one.

In computational complexity theory, a computational problem H is called NP-hard if, for every problem L which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from L to H. That is, assuming a solution for H takes 1 unit time, H's solution can be used to solve L in polynomial time. As a consequence, finding a polynomial time algorithm to solve a single NP-hard problem would give polynomial time algorithms for all the problems in the complexity class NP. As it is suspected that P≠NP, it is unlikely that such an algorithm exists. It is suspected that there are no polynomial-time algorithms for NP-hard problems, but that has not been proven. A simple example of an NP-hard problem is the subset sum problem.

A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.

In graph theory, a branch of mathematics and computer science, Guan's route problem, the Chinese postman problem, postman tour or route inspection problem is to find a shortest closed path or circuit that visits every edge of an (connected) undirected graph at least once. When the graph has an Eulerian circuit, that circuit is an optimal solution. Otherwise, the optimization problem is to find the smallest number of graph edges to duplicate so that the resulting multigraph does have an Eulerian circuit. It can be solved in polynomial time, unlike the Travelling Salesman Problem which is NP-hard. It is different from the Travelling Salesman Problem in that the travelling salesman cannot repeat visited nodes.
The Bottleneck traveling salesman problem is a problem in discrete or combinatorial optimization. The problem is to find the Hamiltonian cycle in a weighted graph which minimizes the weight of the highest-weight edge of the cycle. It was first formulated by Gilmore & Gomory (1964) with some additional constraints, and in its full generality by Garfinkel & Gilbert (1978).

Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there are also many approximation algorithms that provide an additive guarantee on the quality of the returned solution. A notable example of an approximation algorithm that provides both is the classic approximation algorithm of Lenstra, Shmoys and Tardos for scheduling on unrelated parallel machines.
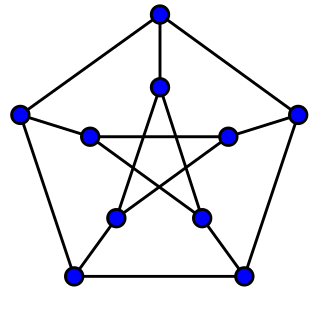
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.
The quadratic assignment problem (QAP) is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems first introduced by Koopmans and Beckmann.

A combinatorial auction is a type of smart market in which participants can place bids on combinations of discrete heterogeneous items, or “packages”, rather than individual items or continuous quantities. These packages can be also called lots and the whole auction a multi-lot auction. Combinatorial auctions are applicable when bidders have non-additive valuations on bundles of items, that is, they value combinations of items more or less than the sum of the valuations of individual elements of the combination.

Václav (Vašek) Chvátal is a Professor Emeritus in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Quebec, Canada, and a visiting professor at Charles University in Prague. He has published extensively on topics in graph theory, combinatorics, and combinatorial optimization.
An integer relation between a set of real numbers x1, x2, ..., xn and a set of integers a1, a2, ..., an, not all 0, such that
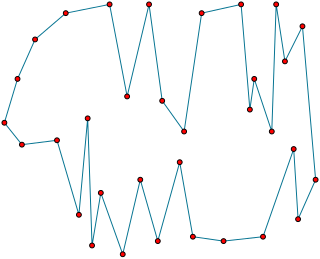
In computational geometry, a bitonic tour of a set of point sites in the Euclidean plane is a closed polygonal chain that has each site as one of its vertices, such that any vertical line crosses the chain at most twice.
The Concorde TSP Solver is a program for solving the travelling salesman problem. It was written by David Applegate, Robert E. Bixby, Vašek Chvátal, and William J. Cook, in ANSI C, and is freely available for academic use.

Alexander Hendrik George Rinnooy Kan is a Dutch politician, businessman and mathematician who served as Chairman of the Social and Economic Council from 2006 to 2012. A member of the Democrats 66 (D66) party, he was a member of the Senate from 2015 to 2019 and is a distinguished professor of Economics and Business Studies at the University of Amsterdam since 1 September 2012. He has also been president of the supervisory board of EYE Film Institute Netherlands since 2008 and of Museum Boerhaave since 2018.
Eugene Leighton (Gene) Lawler was an American computer scientist and a professor of computer science at the University of California, Berkeley.

William John Cook is an American operations researcher and mathematician, and Professor of Combinatorics and Optimization at the University of Waterloo.
David L. Applegate is an American computer scientist known for his research on the traveling salesperson problem.











