Related Research Articles

Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

A shape is a graphical representation of an object's form or its external boundary, outline, or external surface; it is distinct from other object properties, such as color, texture, or material type. In geometry, shape excludes information about the object's location, scale, orientation and reflection. A figure is a representation including both shape and size.

In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.
In geometry, an equilateral polygon is a polygon which has all sides of the same length. Except in the triangle case, an equilateral polygon does not need to also be equiangular, but if it does then it is a regular polygon. If the number of sides is at least five, an equilateral polygon does not need to be a convex polygon: it could be concave or even self-intersecting.

In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of equal measure, or as a trapezoid whose diagonals have equal length. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides are parallel, and the two other sides are of equal length, and the diagonals have equal length. The base angles of an isosceles trapezoid are equal in measure.

A Reuleaux triangle is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four sides of equal length and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ABCD would be denoted ABCD.

In geometry, lines in a plane or higher-dimensional space are concurrent if they intersect at a single point.

In geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figure F is inscribed in figure G" means precisely the same thing as "figure G is circumscribed about figure F". A circle or ellipse inscribed in a convex polygon is tangent to every side or face of the outer figure. A polygon inscribed in a circle, ellipse, or polygon has each vertex on the outer figure; if the outer figure is a polygon or polyhedron, there must be a vertex of the inscribed polygon or polyhedron on each side of the outer figure. An inscribed figure is not necessarily unique in orientation; this can easily be seen, for example, when the given outer figure is a circle, in which case a rotation of an inscribed figure gives another inscribed figure that is congruent to the original one.

In geometry, an antiparallelogram is a type of self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general parallel. Instead, each pair of sides is antiparallel with respect to the other, with sides in the longer pair crossing each other as in a scissors mechanism. Whereas a parallelogram's opposite angles are equal and oriented the same way, an antiparallelogram's are equal but oppositely oriented. Antiparallelograms are also called contraparallelograms or crossed parallelograms.
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.
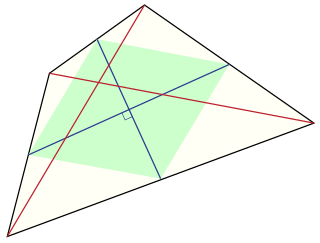
In Euclidean geometry, an equidiagonal quadrilateral is a convex quadrilateral whose two diagonals have equal length. Equidiagonal quadrilaterals were important in ancient Indian mathematics, where quadrilaterals were classified first according to whether they were equidiagonal and then into more specialized types.

In Euclidean geometry, a tangential polygon, also known as a circumscribed polygon, is a convex polygon that contains an inscribed circle. This is a circle that is tangent to each of the polygon's sides. The dual polygon of a tangential polygon is a cyclic polygon, which has a circumscribed circle passing through each of its vertices.