In machine learning, support vector machines are supervised max-margin models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories by Vladimir Vapnik with colleagues SVMs are one of the most studied models, being based on statistical learning frameworks or VC theory proposed by Vapnik and Chervonenkis (1974).

In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
- With a shape parameter k and a scale parameter θ
- With a shape parameter and an inverse scale parameter , called a rate parameter.
In mathematics, the Riemann–Liouville integral associates with a real function another function Iαf of the same kind for each value of the parameter α > 0. The integral is a manner of generalization of the repeated antiderivative of f in the sense that for positive integer values of α, Iαf is an iterated antiderivative of f of order α. The Riemann–Liouville integral is named for Bernhard Riemann and Joseph Liouville, the latter of whom was the first to consider the possibility of fractional calculus in 1832. The operator agrees with the Euler transform, after Leonhard Euler, when applied to analytic functions. It was generalized to arbitrary dimensions by Marcel Riesz, who introduced the Riesz potential.
Multi-task learning (MTL) is a subfield of machine learning in which multiple learning tasks are solved at the same time, while exploiting commonalities and differences across tasks. This can result in improved learning efficiency and prediction accuracy for the task-specific models, when compared to training the models separately. Early versions of MTL were called "hints".
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the linear rotor requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water, ammonia, or methane.
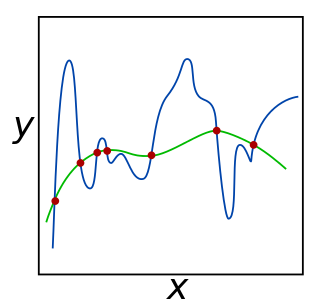
In mathematics, statistics, finance, computer science, particularly in machine learning and inverse problems, regularization is a process that changes the result answer to be "simpler". It is often used to obtain results for ill-posed problems or to prevent overfitting.
The Wigner D-matrix is a unitary matrix in an irreducible representation of the groups SU(2) and SO(3). It was introduced in 1927 by Eugene Wigner, and plays a fundamental role in the quantum mechanical theory of angular momentum. The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotors. The letter D stands for Darstellung, which means "representation" in German.
Linear Programming Boosting (LPBoost) is a supervised classifier from the boosting family of classifiers. LPBoost maximizes a margin between training samples of different classes and hence also belongs to the class of margin-maximizing supervised classification algorithms. Consider a classification function
Gradient boosting is a machine learning technique based on boosting in a functional space, where the target is pseudo-residuals rather than the typical residuals used in traditional boosting. It gives a prediction model in the form of an ensemble of weak prediction models, i.e., models that make very few assumptions about the data, which are typically simple decision trees. When a decision tree is the weak learner, the resulting algorithm is called gradient-boosted trees; it usually outperforms random forest. A gradient-boosted trees model is built in a stage-wise fashion as in other boosting methods, but it generalizes the other methods by allowing optimization of an arbitrary differentiable loss function.
In mathematics, the Kodaira–Spencer map, introduced by Kunihiko Kodaira and Donald C. Spencer, is a map associated to a deformation of a scheme or complex manifold X, taking a tangent space of a point of the deformation space to the first cohomology group of the sheaf of vector fields on X.

In physics, relativistic angular momentum refers to the mathematical formalisms and physical concepts that define angular momentum in special relativity (SR) and general relativity (GR). The relativistic quantity is subtly different from the three-dimensional quantity in classical mechanics.
Proximal gradientmethods for learning is an area of research in optimization and statistical learning theory which studies algorithms for a general class of convex regularization problems where the regularization penalty may not be differentiable. One such example is regularization of the form
In machine learning, the kernel embedding of distributions comprises a class of nonparametric methods in which a probability distribution is represented as an element of a reproducing kernel Hilbert space (RKHS). A generalization of the individual data-point feature mapping done in classical kernel methods, the embedding of distributions into infinite-dimensional feature spaces can preserve all of the statistical features of arbitrary distributions, while allowing one to compare and manipulate distributions using Hilbert space operations such as inner products, distances, projections, linear transformations, and spectral analysis. This learning framework is very general and can be applied to distributions over any space on which a sensible kernel function may be defined. For example, various kernels have been proposed for learning from data which are: vectors in , discrete classes/categories, strings, graphs/networks, images, time series, manifolds, dynamical systems, and other structured objects. The theory behind kernel embeddings of distributions has been primarily developed by Alex Smola, Le Song , Arthur Gretton, and Bernhard Schölkopf. A review of recent works on kernel embedding of distributions can be found in.

The theory of causal fermion systems is an approach to describe fundamental physics. It provides a unification of the weak, the strong and the electromagnetic forces with gravity at the level of classical field theory. Moreover, it gives quantum mechanics as a limiting case and has revealed close connections to quantum field theory. Therefore, it is a candidate for a unified physical theory. Instead of introducing physical objects on a preexisting spacetime manifold, the general concept is to derive spacetime as well as all the objects therein as secondary objects from the structures of an underlying causal fermion system. This concept also makes it possible to generalize notions of differential geometry to the non-smooth setting. In particular, one can describe situations when spacetime no longer has a manifold structure on the microscopic scale. As a result, the theory of causal fermion systems is a proposal for quantum geometry and an approach to quantum gravity.
Multiple kernel learning refers to a set of machine learning methods that use a predefined set of kernels and learn an optimal linear or non-linear combination of kernels as part of the algorithm. Reasons to use multiple kernel learning include a) the ability to select for an optimal kernel and parameters from a larger set of kernels, reducing bias due to kernel selection while allowing for more automated machine learning methods, and b) combining data from different sources that have different notions of similarity and thus require different kernels. Instead of creating a new kernel, multiple kernel algorithms can be used to combine kernels already established for each individual data source.
Regularized least squares (RLS) is a family of methods for solving the least-squares problem while using regularization to further constrain the resulting solution.
In statistical learning theory, a learnable function class is a set of functions for which an algorithm can be devised to asymptotically minimize the expected risk, uniformly over all probability distributions. The concept of learnable classes are closely related to regularization in machine learning, and provides large sample justifications for certain learning algorithms.
The convolutional sparse coding paradigm is an extension of the global sparse coding model, in which a redundant dictionary is modeled as a concatenation of circulant matrices. While the global sparsity constraint describes signal as a linear combination of a few atoms in the redundant dictionary , usually expressed as for a sparse vector , the alternative dictionary structure adopted by the convolutional sparse coding model allows the sparsity prior to be applied locally instead of globally: independent patches of are generated by "local" dictionaries operating over stripes of .
Weak supervision is a paradigm in machine learning, the relevance and notability of which increased with the advent of large language models due to large amount of data required to train them. It is characterized by using a combination of a small amount of human-labeled data, followed by a large amount of unlabeled data. In other words, the desired output values are provided only for a subset of the training data. The remaining data is unlabeled or imprecisely labeled. Intuitively, it can be seen as an exam and labeled data as sample problems that the teacher solves for the class as an aid in solving another set of problems. In the transductive setting, these unsolved problems act as exam questions. In the inductive setting, they become practice problems of the sort that will make up the exam. Technically, it could be viewed as performing clustering and then labeling the clusters with the labeled data, pushing the decision boundary away from high-density regions, or learning an underlying one-dimensional manifold where the data reside.
In complex geometry, the lemma is a mathematical lemma about the de Rham cohomology class of a complex differential form. The -lemma is a result of Hodge theory and the Kähler identities on a compact Kähler manifold. Sometimes it is also known as the -lemma, due to the use of a related operator , with the relation between the two operators being and so .







































































