Monodromy

Last updated July 14, 2023

In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology, algebraic geometry and differential geometry behave as they "run round" a singularity. As the name implies, the fundamental meaning of monodromy comes from "running round singly". It is closely associated with covering maps and their degeneration into ramification; the aspect giving rise to monodromy phenomena is that certain functions we may wish to define fail to be single-valued as we "run round" a path encircling a singularity. The failure of monodromy can be measured by defining a monodromy group: a group of transformations acting on the data that encodes what happens as we "run round" in one dimension. Lack of monodromy is sometimes called polydromy.^[1]

Definition

Let $X$ be a connected and locally connected based topological space with base point $x$ , and let $p:{\tilde {X}}\to X$ be a covering with fiber $F=p^{-1}(x)$ . For a loop $γ: [0, 1] \to X$ based at $x$ , denote a lift under the covering map, starting at a point ${\tilde {x}}\in F$ , by ${\tilde {\gamma }}$ . Finally, we denote by ${\tilde {x}}\cdot {\tilde {\gamma }}$ the endpoint ${\tilde {\gamma }}(1)$ , which is generally different from ${\tilde {x}}$ . There are theorems which state that this construction gives a well-defined group action of the fundamental group $π 1 (X, x)$ on $F$ , and that the stabilizer of ${\tilde {x}}$ is exactly $p_{*}\left(\pi _{1}\left({\tilde {X}},{\tilde {x}}\right)\right)$ , that is, an element $[γ]$ fixes a point in $F$ if and only if it is represented by the image of a loop in ${\tilde {X}}$ based at ${\tilde {x}}$ . This action is called the monodromy action and the corresponding homomorphism $π 1 (X, x) \to Aut(H * (F x))$ into the automorphism group on $F$ is the algebraic monodromy. The image of this homomorphism is the monodromy group. There is another map $π 1 (X, x) \to Diff(F x)/Is(F x)$ whose image is called the topological monodromy group.

Example

These ideas were first made explicit in complex analysis. In the process of analytic continuation, a function that is an analytic function $F (z)$ in some open subset $E$ of the punctured complex plane $\mathbb {C} \backslash \{0\}$ may be continued back into $E$ , but with different values. For example, take

{\begin{aligned}F(z)&=\log(z)\\E&=\{z\in \mathbb {C} \mid \operatorname {Re} (z)>0\}\end{aligned}}

then analytic continuation anti-clockwise round the circle

|z|=1

will result in the return, not to $F (z)$ but

F(z)+2\pi i

In this case the monodromy group is infinite cyclic and the covering space is the universal cover of the punctured complex plane. This cover can be visualized as the helicoid (as defined in the helicoid article) restricted to $ρ > 0$ . The covering map is a vertical projection, in a sense collapsing the spiral in the obvious way to get a punctured plane.

Differential equations in the complex domain

One important application is to differential equations, where a single solution may give further linearly independent solutions by analytic continuation. Linear differential equations defined in an open, connected set S in the complex plane have a monodromy group, which (more precisely) is a linear representation of the fundamental group of S, summarising all the analytic continuations round loops within S. The inverse problem, of constructing the equation (with regular singularities), given a representation, is called the Riemann–Hilbert problem.

For a regular (and in particular Fuchsian) linear system one usually chooses as generators of the monodromy group the operators M_j corresponding to loops each of which circumvents just one of the poles of the system counterclockwise. If the indices j are chosen in such a way that they increase from 1 to p + 1 when one circumvents the base point clockwise, then the only relation between the generators is the equality $M_{1}\cdots M_{p+1}=\operatorname {id}$ . The Deligne–Simpson problem is the following realisation problem: For which tuples of conjugacy classes in GL(n, C) do there exist irreducible tuples of matrices M_j from these classes satisfying the above relation? The problem has been formulated by Pierre Deligne and Carlos Simpson was the first to obtain results towards its resolution. An additive version of the problem about residua of Fuchsian systems has been formulated and explored by Vladimir Kostov. The problem has been considered by other authors for matrix groups other than GL(n, C) as well.^[2]

Topological and geometric aspects

In the case of a covering map, we look at it as a special case of a fibration, and use the homotopy lifting property to "follow" paths on the base space X (we assume it path-connected for simplicity) as they are lifted up into the cover C. If we follow round a loop based at x in X, which we lift to start at c above x, we'll end at some c* again above x; it is quite possible that c ≠ c*, and to code this one considers the action of the fundamental group $π$ ₁(X, x) as a permutation group on the set of all c, as a monodromy group in this context.

In differential geometry, an analogous role is played by parallel transport. In a principal bundle B over a smooth manifold M, a connection allows "horizontal" movement from fibers above m in M to adjacent ones. The effect when applied to loops based at m is to define a holonomy group of translations of the fiber at m; if the structure group of B is G, it is a subgroup of G that measures the deviation of B from the product bundle M × G.

Monodromy groupoid and foliations

Analogous to the fundamental groupoid it is possible to get rid of the choice of a base point and to define a monodromy groupoid. Here we consider (homotopy classes of) lifts of paths in the base space X of a fibration $p:{\tilde {X}}\to X$ . The result has the structure of a groupoid over the base space X. The advantage is that we can drop the condition of connectedness of X.

Moreover the construction can also be generalized to foliations: Consider $(M,{\mathcal {F}})$ a (possibly singular) foliation of M. Then for every path in a leaf of ${\mathcal {F}}$ we can consider its induced diffeomorphism on local transversal sections through the endpoints. Within a simply connected chart this diffeomorphism becomes unique and especially canonical between different transversal sections if we go over to the germ of the diffeomorphism around the endpoints. In this way it also becomes independent of the path (between fixed endpoints) within a simply connected chart and is therefore invariant under homotopy.

Definition via Galois theory

Let F(x) denote the field of the rational functions in the variable x over the field F, which is the field of fractions of the polynomial ring F[x]. An element y = f(x) of F(x) determines a finite field extension [F(x) : F(y)].

This extension is generally not Galois but has Galois closure L(f). The associated Galois group of the extension [L(f) : F(y)] is called the monodromy group of f.

In the case of F = C Riemann surface theory enters and allows for the geometric interpretation given above. In the case that the extension [C(x) : C(y)] is already Galois, the associated monodromy group is sometimes called a group of deck transformations.

This has connections with the Galois theory of covering spaces leading to the Riemann existence theorem.

Notes

↑ König, Wolfgang; Sprekels, Jürgen (2015). Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes – Aspects of his Life and Work (in German). Springer-Verlag. pp. 200–201. ISBN 9783658106195 . Retrieved 5 October 2017.
↑ V. P. Kostov (2004), "The Deligne–Simpson problem — a survey", J. Algebra, 281 (1): 83–108, arXiv: math/0206298 , doi:10.1016/j.jalgebra.2004.07.013, MR 2091962, S2CID 119634752 and the references therein.

Related Research Articles

In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent have isomorphic fundamental groups. The fundamental group of a topological space $is denoted by .$

In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:

A covering of a topological space $is a continuous map with special properties.$

In the mathematical disciplines of topology and geometry, an orbifold is a generalization of a manifold. Roughly speaking, an orbifold is a topological space which is locally a finite group quotient of a Euclidean space.

In mathematics, a Lie algebroid is a vector bundle $together with a Lie bracket on its space of sections and a vector bundle morphism, satisfying a Leibniz rule. A Lie algebroid can thus be thought of as a "many-object generalisation" of a Lie algebra.$

In mathematics, a Lie groupoid is a groupoid where the set $of objects and the set of morphisms are both manifolds, all the category operations are smooth, and the source and target operations$

<span class="mw-page-title-main">Foliation</span> In mathematics, a type of equivalence relation on an n-manifold

In mathematics, a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rⁿ into the cosets x + R^p of the standardly embedded subspace R^p. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable, or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class C^r it is usually understood that r ≥ 1. The number p is called the dimension of the foliation and q = n − p is called its codimension.

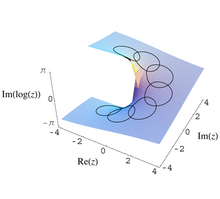
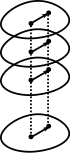
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that if the function is n-valued at that point, all of its neighborhoods contain a point that has more than n values. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept.

In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence $of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group . These concepts are named after the mathematician J. H. C. Whitehead.$

In mathematics, the Teichmüller space $of a (real) topological surface, is a space that parametrizes complex structures on up to the action of homeomorphisms that are isotopic to the identity homeomorphism. Teichmüller spaces are named after Oswald Teichmüller.$

In mathematics, a local system on a topological space X is a tool from algebraic topology which interpolates between cohomology with coefficients in a fixed abelian group A, and general sheaf cohomology in which coefficients vary from point to point. Local coefficient systems were introduced by Norman Steenrod in 1943.

In geometric group theory and dynamical systems the iterated monodromy group of a covering map is a group describing the monodromy action of the fundamental group on all iterations of the covering. A single covering map between spaces is therefore used to create a tower of coverings, by placing the covering over itself repeatedly. In terms of the Galois theory of covering spaces, this construction on spaces is expected to correspond to a construction on groups. The iterated monodromy group provides this construction, and it is applied to encode the combinatorics and symbolic dynamics of the covering, and provide examples of self-similar groups.

In mathematics, the term Riemann–Hilbert correspondence refers to the correspondence between regular singular flat connections on algebraic vector bundles and representations of the fundamental group, and more generally to one of several generalizations of this. The original setting appearing in Hilbert's twenty-first problem was for the Riemann sphere, where it was about the existence of systems of linear regular differential equations with prescribed monodromy representations. First the Riemann sphere may be replaced by an arbitrary Riemann surface and then, in higher dimensions, Riemann surfaces are replaced by complex manifolds of dimension > 1. There is a correspondence between certain systems of partial differential equations and possible monodromies of their solutions.

In complex analysis, the monodromy theorem is an important result about analytic continuation of a complex-analytic function to a larger set. The idea is that one can extend a complex-analytic function along curves starting in the original domain of the function and ending in the larger set. A potential problem of this analytic continuation along a curve strategy is there are usually many curves which end up at the same point in the larger set. The monodromy theorem gives sufficient conditions for analytic continuation to give the same value at a given point regardless of the curve used to get there, so that the resulting extended analytic function is well-defined and single-valued.

In the mathematical subject of group theory, the Grushko theorem or the Grushko–Neumann theorem is a theorem stating that the rank of a free product of two groups is equal to the sum of the ranks of the two free factors. The theorem was first obtained in a 1940 article of Grushko and then, independently, in a 1943 article of Neumann.

In the mathematical theory of special functions, Schwarz's list or the Schwartz table is the list of 15 cases found by Hermann Schwarz when hypergeometric functions can be expressed algebraically. More precisely, it is a listing of parameters determining the cases in which the hypergeometric equation has a finite monodromy group, or equivalently has two independent solutions that are algebraic functions. It lists 15 cases, divided up by the isomorphism class of the monodromy group, and was first derived by Schwarz by methods of complex analytic geometry. Correspondingly the statement is not directly in terms of the parameters specifying the hypergeometric equation, but in terms of quantities used to describe certain spherical triangles.

In mathematics, and more precisely in topology, the mapping class group of a surface, sometimes called the modular group or Teichmüller modular group, is the group of homeomorphisms of the surface viewed up to continuous deformation. It is of fundamental importance for the study of 3-manifolds via their embedded surfaces and is also studied in algebraic geometry in relation to moduli problems for curves.

In mathematics, Picard–Lefschetz theory studies the topology of a complex manifold by looking at the critical points of a holomorphic function on the manifold. It was introduced by Émile Picard for complex surfaces in his book Picard & Simart (1897), and extended to higher dimensions by Solomon Lefschetz (1924). It is a complex analog of Morse theory that studies the topology of a real manifold by looking at the critical points of a real function. Pierre Deligne and Nicholas Katz (1973) extended Picard–Lefschetz theory to varieties over more general fields, and Deligne used this generalization in his proof of the Weil conjectures.

In geometry, if X is a manifold with an action of a topological group G by analytical diffeomorphisms, the notion of a (G, X)-structure on a topological space is a way to formalise it being locally isomorphic to X with its G-invariant structure; spaces with a (G, X)-structure are always manifolds and are called (G, X)-manifolds. This notion is often used with G being a Lie group and X a homogeneous space for G. Foundational examples are hyperbolic manifolds and affine manifolds.

In the ADM formulation of general relativity one splits spacetime into spatial slices and time, the basic variables are taken to be the induced metric, $, on the spatial slice, and its conjugate momentum variable related to the extrinsic curvature,,. These are the metric canonical coordinates.$

References

V. I. Danilov (2001) [1994], "Monodromy", Encyclopedia of Mathematics , EMS Press
"Group-groupoids and monodromy groupoids", O. Mucuk, B. Kılıçarslan, T. ¸Sahan, N. Alemdar, Topology and its Applications 158 (2011) 2034–2042 doi:10.1016/j.topol.2011.06.048
R. Brown Topology and Groupoids (2006).
P.J. Higgins, "Categories and groupoids", van Nostrand (1971) TAC Reprint
H. Żołądek, "The Monodromy Group", Birkhäuser Basel 2006; doi: 10.1007/3-7643-7536-1

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[König2015-1] König, Wolfgang; Sprekels, Jürgen (2015). Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes – Aspects of his Life and Work (in German). Springer-Verlag. pp. 200–201. ISBN 9783658106195 . Retrieved 5 October 2017.

[2] V. P. Kostov (2004), "The Deligne–Simpson problem — a survey", J. Algebra, 281 (1): 83–108, arXiv: math/0206298 , doi:10.1016/j.jalgebra.2004.07.013, MR 2091962, S2CID 119634752 and the references therein.

[1]

[2]