In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:
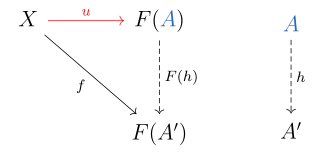
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In category theory, a branch of mathematics, an enriched category generalizes the idea of a category by replacing hom-sets with objects from a general monoidal category. It is motivated by the observation that, in many practical applications, the hom-set often has additional structure that should be respected, e.g., that of being a vector space of morphisms, or a topological space of morphisms. In an enriched category, the set of morphisms associated with every pair of objects is replaced by an object in some fixed monoidal category of "hom-objects". In order to emulate the (associative) composition of morphisms in an ordinary category, the hom-category must have a means of composing hom-objects in an associative manner: that is, there must be a binary operation on objects giving us at least the structure of a monoidal category, though in some contexts the operation may also need to be commutative and perhaps also to have a right adjoint.
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions. Many important categories have obvious interpretations as concrete categories, for example the category of topological spaces and the category of groups, and trivially also the category of sets itself. On the other hand, the homotopy category of topological spaces is not concretizable, i.e. it does not admit a faithful functor to the category of sets.
In category theory, a branch of mathematics, a monad is a monoid in the category of endofunctors. An endofunctor is a functor mapping a category to itself, and a monad is an endofunctor together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories. Monads are also useful in the theory of datatypes and in functional programming languages, allowing languages with non-mutable states to do things such as simulate for-loops; see Monad.
In category theory, a branch of mathematics, a functor category is a category where the objects are the functors and the morphisms are natural transformations between the functors. Functor categories are of interest for two main reasons:
In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere, although the technique did not become generally known until many years later. Several mathematical concepts can be treated as comma categories. Comma categories also guarantee the existence of some limits and colimits. The name comes from the notation originally used by Lawvere, which involved the comma punctuation mark. The name persists even though standard notation has changed, since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category".
In mathematics, the derived categoryD(A) of an abelian category A is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on A. The construction proceeds on the basis that the objects of D(A) should be chain complexes in A, with two such chain complexes considered isomorphic when there is a chain map that induces an isomorphism on the level of homology of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hypercohomology. The definitions lead to a significant simplification of formulas otherwise described (not completely faithfully) by complicated spectral sequences.
Fibred categories are abstract entities in mathematics used to provide a general framework for descent theory. They formalise the various situations in geometry and algebra in which inverse images of objects such as vector bundles can be defined. As an example, for each topological space there is the category of vector bundles on the space, and for every continuous map from a topological space X to another topological space Y is associated the pullback functor taking bundles on Y to bundles on X. Fibred categories formalise the system consisting of these categories and inverse image functors. Similar setups appear in various guises in mathematics, in particular in algebraic geometry, which is the context in which fibred categories originally appeared. Fibered categories are used to define stacks, which are fibered categories with "descent". Fibrations also play an important role in categorical semantics of type theory, and in particular that of dependent type theories.
This is a glossary of properties and concepts in category theory in mathematics.
In category theory, a Kleisli category is a category naturally associated to any monad T. It is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the Eilenberg–Moore category. Kleisli categories are named for the mathematician Heinrich Kleisli.
In category theory, a monoidal monad is a monad on a monoidal category such that the functor is a lax monoidal functor and the natural transformations and are monoidal natural transformations. In other words, is equipped with coherence maps and satisfying certain properties, and the unit and multiplication are monoidal natural transformations. By monoidality of , the morphisms and are necessarily equal.
In category theory, a branch of mathematics, the diagonal functor is given by , which maps objects as well as morphisms. This functor can be employed to give a succinct alternate description of the product of objects within the category : a product is a universal arrow from to . The arrow comprises the projection maps.
In homological algebra, the hyperhomology or hypercohomology is a generalization of (co)homology functors which takes as input not objects in an abelian category but instead chain complexes of objects, so objects in . It is a sort of cross between the derived functor cohomology of an object and the homology of a chain complex since hypercohomology corresponds to the derived global sections functor .
In mathematics, mixed Hodge modules are the culmination of Hodge theory, mixed Hodge structures, intersection cohomology, and the decomposition theorem yielding a coherent framework for discussing variations of degenerating mixed Hodge structures through the six functor formalism. Essentially, these objects are a pair of a filtered D-module together with a perverse sheaf such that the functor from the Riemann–Hilbert correspondence sends to . This makes it possible to construct a Hodge structure on intersection cohomology, one of the key problems when the subject was discovered. This was solved by Morihiko Saito who found a way to use the filtration on a coherent D-module as an analogue of the Hodge filtration for a Hodge structure. This made it possible to give a Hodge structure on an intersection cohomology sheaf, the simple objects in the Abelian category of perverse sheaves.
In mathematics a stack or 2-sheaf is, roughly speaking, a sheaf that takes values in categories rather than sets. Stacks are used to formalise some of the main constructions of descent theory, and to construct fine moduli stacks when fine moduli spaces do not exist.
In mathematics, the quotient of an abelian category by a Serre subcategory is the abelian category which, intuitively, is obtained from by ignoring all objects from . There is a canonical exact functor whose kernel is , and is in a certain sense the most general abelian category with this property.
In mathematics, an Abelian 2-group is a higher dimensional analogue of an Abelian group, in the sense of higher algebra, which were originally introduced by Alexander Grothendieck while studying abstract structures surrounding Abelian varieties and Picard groups. More concretely, they are given by groupoids which have a bifunctor which acts formally like the addition an Abelian group. Namely, the bifunctor has a notion of commutativity, associativity, and an identity structure. Although this seems like a rather lofty and abstract structure, there are several examples of Abelian 2-groups. In fact, some of which provide prototypes for more complex examples of higher algebraic structures, such as Abelian n-groups.