The Rulkov map is a two-dimensional iterated map used to model a biological neuron. It was proposed by Nikolai F. Rulkov in 2001. [1] The use of this map to study neural networks has computational advantages because the map is easier to iterate than a continuous dynamical system. This saves memory and simplifies the computation of large neural networks.
The Rulkov map, with as discrete time, can be represented by the following dynamical equations:
where represents the membrane potential of the neuron. The variable in the model is a slow variable due to a very small value of . Unlike variable , variable does not have explicit biological meaning, though some analogy to gating variables can be drawn. [2] The parameter can be thought of as an external dc current given to the neuron and is a nonlinearity parameter of the map. Different combinations of parameters and give rise to different dynamical states of the neuron like resting, tonic spiking and chaotic bursts. The chaotic bursting is enabled above
The dynamics of the Rulkov map can be analyzed by analyzing the dynamics of its one dimensional fast submap. Since the variable evolves very slowly, for moderate amount of time it can be treated as a parameter with constant value in the variable's evolution equation (which we now call as one dimensional fast submap because as compared to , is a fast variable). Depending on the value of , this submap can have either one or three fixed points. One of these fixed points is stable, another is unstable and third may change the stability. [3] As increases, two of these fixed points (stable one and unstable one) merge and disappear by saddle-node bifurcation.
Coupling of two neurons has been investigated by Irina Bashkirtseva and Alexander Pisarchik who explored transitions between stationary, periodic, quasiperiodic, and chaotic regimes. [4] They also addresses the additional consequences of random disturbances on this system, leading to noise-induced transitions between periodic and chaotic stochastic oscillations. [5]
Adaptations of the Rulkov map have found applications in labor and industrial economics, particularly in the realm of corporate dynamics. [6] The proposed framework leverages synchronization and chaos regularization to account for dynamic transitions among multiple equilibria, incorporate skewness and idiosyncratic elements, and unveil the influence of effort on corporate profitability. The results are substantiated through empirical validation with real-world data. [6] Orlando and Bufalo introduced a deterministic model based on the Rulkov map, [7] effectively modeling volatility fluctuations in corporate yields and spreads, even during distressed periods like COVID-19. Comparing it to the ARIMA-EGARCH model, designed for handling various volatility aspects, both models yield comparable results. Nevertheless, the deterministic nature of the Rulkov map model may provide enhanced explanatory capabilities. [8]
Other applications of the Rulkov map include memristors, [9] [10] financial markets, [11] [12] biological systems, [13] etc.
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state.
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Texas can cause a tornado in Brazil.
A complex system is a system composed of many components which may interact with each other. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication systems, complex software and electronic systems, social and economic organizations, an ecosystem, a living cell, and ultimately the entire universe.
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.
An artificial neuron is a mathematical function conceived as a model of biological neurons in a neural network. Artificial neurons are the elementary units of artificial neural networks. The artificial neuron receives one or more inputs and sums them to produce an output. Usually, each input is separately weighted, and the sum is often added to a term known as a bias, before being passed through a non-linear function known as an activation function or transfer function. The transfer functions usually have a sigmoid shape, but they may also take the form of other non-linear functions, piecewise linear functions, or step functions. They are also often monotonically increasing, continuous, differentiable and bounded. Non-monotonic, unbounded and oscillating activation functions with multiple zeros that outperform sigmoidal and ReLU-like activation functions on many tasks have also been recently explored. The thresholding function has inspired building logic gates referred to as threshold logic; applicable to building logic circuits resembling brain processing. For example, new devices such as memristors have been extensively used to develop such logic in recent times.
In the study of dynamical systems, a delay embedding theorem gives the conditions under which a chaotic dynamical system can be reconstructed from a sequence of observations of the state of that system. The reconstruction preserves the properties of the dynamical system that do not change under smooth coordinate changes, but it does not preserve the geometric shape of structures in phase space.
A Hopfield network is a form of recurrent artificial neural network and a type of spin glass system popularised by John Hopfield in 1982 as described by Shun'ichi Amari in 1972 and by Little in 1974 based on Ernst Ising's work with Wilhelm Lenz on the Ising model. Hopfield networks serve as content-addressable ("associative") memory systems with binary threshold nodes, or with continuous variables. Hopfield networks also provide a model for understanding human memory.
The Granger causality test is a statistical hypothesis test for determining whether one time series is useful in forecasting another, first proposed in 1969. Ordinarily, regressions reflect "mere" correlations, but Clive Granger argued that causality in economics could be tested for by measuring the ability to predict the future values of a time series using prior values of another time series. Since the question of "true causality" is deeply philosophical, and because of the post hoc ergo propter hoc fallacy of assuming that one thing preceding another can be used as a proof of causation, econometricians assert that the Granger test finds only "predictive causality". Using the term "causality" alone is a misnomer, as Granger-causality is better described as "precedence", or, as Granger himself later claimed in 1977, "temporally related". Rather than testing whether Xcauses Y, the Granger causality tests whether X forecastsY.
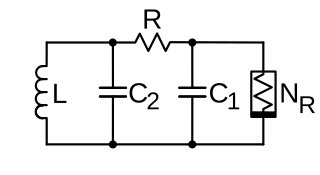
Chua's circuit is a simple electronic circuit that exhibits classic chaotic behavior. This means roughly that it is a "nonperiodic oscillator"; it produces an oscillating waveform that, unlike an ordinary electronic oscillator, never "repeats". It was invented in 1983 by Leon O. Chua, who was a visitor at Waseda University in Japan at that time. The ease of construction of the circuit has made it a ubiquitous real-world example of a chaotic system, leading some to declare it "a paradigm for chaos".
Bursting, or burst firing, is an extremely diverse general phenomenon of the activation patterns of neurons in the central nervous system and spinal cord where periods of rapid action potential spiking are followed by quiescent periods much longer than typical inter-spike intervals. Bursting is thought to be important in the operation of robust central pattern generators, the transmission of neural codes, and some neuropathologies such as epilepsy. The study of bursting both directly and in how it takes part in other neural phenomena has been very popular since the beginnings of cellular neuroscience and is closely tied to the fields of neural synchronization, neural coding, plasticity, and attention.
In dynamical systems theory, a period-doubling bifurcation occurs when a slight change in a system's parameters causes a new periodic trajectory to emerge from an existing periodic trajectory—the new one having double the period of the original. With the doubled period, it takes twice as long for the numerical values visited by the system to repeat themselves.
A memristor is a non-linear two-terminal electrical component relating electric charge and magnetic flux linkage. It was described and named in 1971 by Leon Chua, completing a theoretical quartet of fundamental electrical components which also comprises the resistor, capacitor and inductor.
Biological neuron models, also known as spiking neuron models, are mathematical descriptions of neurons. In particular, these models describe how the voltage potential across the cell membrane changes over time. In an experimental setting, stimulating neurons with an electrical current generates an action potential, that propagates down the neuron's axon. This axon can branch out and connect to a large number of downstream neurons at sites called synapses. At these synapses, the spike can cause release of a biochemical substance (neurotransmitter), which in turn can change the voltage potential of downstream neurons, potentially leading to spikes in those downstream neurons, thus propagating the signal. As many as 85% of neurons in the neocortex, the outermost layer of the mammalian brain, consists of excitatory pyramidal neurons, and each pyramidal neuron receives tens of thousands of inputs from other neurons. Thus, spiking neurons are a major information processing unit of the nervous system.
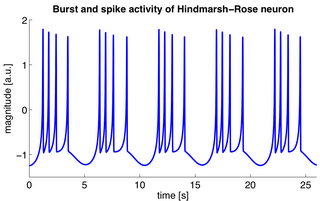
The Hindmarsh–Rose model of neuronal activity is aimed to study the spiking-bursting behavior of the membrane potential observed in experiments made with a single neuron. The relevant variable is the membrane potential, x(t), which is written in dimensionless units. There are two more variables, y(t) and z(t), which take into account the transport of ions across the membrane through the ion channels. The transport of sodium and potassium ions is made through fast ion channels and its rate is measured by y(t), which is called the spiking variable. z(t) corresponds to an adaptation current, which is incremented at every spike, leading to a decrease in the firing rate. Then, the Hindmarsh–Rose model has the mathematical form of a system of three nonlinear ordinary differential equations on the dimensionless dynamical variables x(t), y(t), and z(t). They read:
A coupled map lattice (CML) is a dynamical system that models the behavior of nonlinear systems. They are predominantly used to qualitatively study the chaotic dynamics of spatially extended systems. This includes the dynamics of spatiotemporal chaos where the number of effective degrees of freedom diverges as the size of the system increases.
The dynamical systems approach to neuroscience is a branch of mathematical biology that utilizes nonlinear dynamics to understand and model the nervous system and its functions. In a dynamical system, all possible states are expressed by a phase space. Such systems can experience bifurcation as a function of its bifurcation parameters and often exhibit chaos. Dynamical neuroscience describes the non-linear dynamics at many levels of the brain from single neural cells to cognitive processes, sleep states and the behavior of neurons in large-scale neuronal simulation.
In the context of artificial neural networks, the rectifier or ReLU activation function is an activation function defined as the positive part of its argument:
In biology exponential integrate-and-fire models are compact and computationally efficient nonlinear spiking neuron models with one or two variables. The exponential integrate-and-fire model was first proposed as a one-dimensional model. The most prominent two-dimensional examples are the adaptive exponential integrate-and-fire model and the generalized exponential integrate-and-fire model. Exponential integrate-and-fire models are widely used in the field of computational neuroscience and spiking neural networks because of (i) a solid grounding of the neuron model in the field of experimental neuroscience, (ii) computational efficiency in simulations and hardware implementations, and (iii) mathematical transparency.
Phase reduction is a method used to reduce a multi-dimensional dynamical equation describing a nonlinear limit cycle oscillator into a one-dimensional phase equation. Many phenomena in our world such as chemical reactions, electric circuits, mechanical vibrations, cardiac cells, and spiking neurons are examples of rhythmic phenomena, and can be considered as nonlinear limit cycle oscillators.
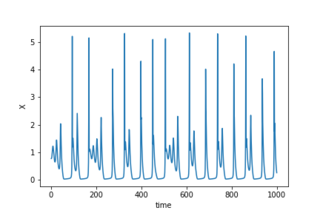
The Chialvo map is a two-dimensional map proposed by Dante R. Chialvo in 1995 to describe the generic dynamics of excitable systems. The model is inspired by Kunihiko Kaneko's Coupled map lattice (CML) numerical approach which considers time and space as discrete variables but state as a continuous one. Later on Rulkov popularized a similar approach. By using only three parameters the model is able to efficiently mimic generic neuronal dynamics in computational simulations, as single elements or as parts of inter-connected networks.
{{cite journal}}: CS1 maint: multiple names: authors list (link){{cite web}}: Missing or empty |title= (help){{cite web}}: Missing or empty |title= (help)