In physics and chemistry, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars.
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function has a root at , then , taking the limit value at , is an entire function. On the other hand, the natural logarithm, the reciprocal function, and the square root are all not entire functions, nor can they be continued analytically to an entire function.
In statistical mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by a conservative force, with that of the total potential energy of the system. Mathematically, the theorem states

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In fluid mechanics, hydrostatic equilibrium is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the planetary atmosphere into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space. In general, it is what causes objects in space to be spherical.
In fluid mechanics, the Grashof number is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number.

The van der Waals equation, named for its originator, the Dutch physicist Johannes Diderik van der Waals, is an equation of state that extends the ideal gas law to include the non-zero size of gas molecules and the interactions between them. As a result the equation is able to model the phase change, liquid vapor. It also produces simple analytic expressions for the properties of real substances that shed light on their behavior. One way to write this equation is:

In electromagnetism, the Mie solution to Maxwell's equations describes the scattering of an electromagnetic plane wave by a homogeneous sphere. The solution takes the form of an infinite series of spherical multipole partial waves. It is named after German physicist Gustav Mie.
The density of air or atmospheric density, denoted ρ, is the mass per unit volume of Earth's atmosphere. Air density, like air pressure, decreases with increasing altitude. It also changes with variations in atmospheric pressure, temperature and humidity. At 101.325 kPa (abs) and 20 °C, air has a density of approximately 1.204 kg/m3 (0.0752 lb/cu ft), according to the International Standard Atmosphere (ISA). At 101.325 kPa (abs) and 15 °C (59 °F), air has a density of approximately 1.225 kg/m3 (0.0765 lb/cu ft), which is about 1⁄800 that of water, according to the International Standard Atmosphere (ISA). Pure liquid water is 1,000 kg/m3 (62 lb/cu ft).
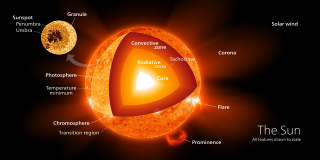
A radiation zone, or radiative region is a layer of a star's interior where energy is primarily transported toward the exterior by means of radiative diffusion and thermal conduction, rather than by convection. Energy travels through the radiation zone in the form of electromagnetic radiation as photons.
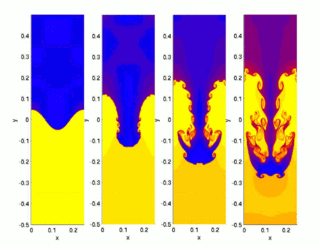
The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.

In atmospheric, earth, and planetary sciences, a scale height, usually denoted by the capital letter H, is a distance over which a physical quantity decreases by a factor of e.

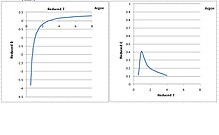
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behaviour. In general, deviation from ideal behaviour becomes more significant the closer a gas is to a phase change, the lower the temperature or the larger the pressure. Compressibility factor values are usually obtained by calculation from equations of state (EOS), such as the virial equation which take compound-specific empirical constants as input. For a gas that is a mixture of two or more pure gases, the gas composition must be known before compressibility can be calculated.
Alternatively, the compressibility factor for specific gases can be read from generalized compressibility charts that plot as a function of pressure at constant temperature.
In physics, the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on Brownian motion. The more general form of the equation in the classical case is
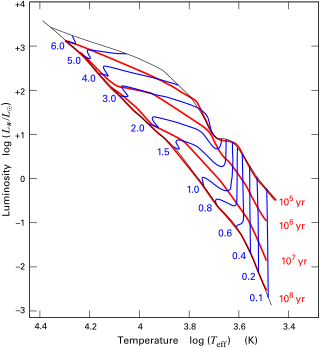
The Hayashi track is a luminosity–temperature relationship obeyed by infant stars of less than 3 M☉ in the pre-main-sequence phase of stellar evolution. It is named after Japanese astrophysicist Chushiro Hayashi. On the Hertzsprung–Russell diagram, which plots luminosity against temperature, the track is a nearly vertical curve. After a protostar ends its phase of rapid contraction and becomes a T Tauri star, it is extremely luminous. The star continues to contract, but much more slowly. While slowly contracting, the star follows the Hayashi track downwards, becoming several times less luminous but staying at roughly the same surface temperature, until either a radiative zone develops, at which point the star starts following the Henyey track, or nuclear fusion begins, marking its entry onto the main sequence.
A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca+ and Sr+ and other ions such as He+, Li2+, and Be3+ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
The shear viscosity of a fluid is a material property that describes the friction between internal neighboring fluid surfaces flowing with different fluid velocities. This friction is the effect of (linear) momentum exchange caused by molecules with sufficient energy to move between these fluid sheets due to fluctuations in their motion. The viscosity is not a material constant, but a material property that depends on temperature, pressure, fluid mixture composition, local velocity variations. This functional relationship is described by a mathematical viscosity model called a constitutive equation which is usually far more complex than the defining equation of shear viscosity. One such complicating feature is the relation between the viscosity model for a pure fluid and the model for a fluid mixture which is called mixing rules. When scientists and engineers use new arguments or theories to develop a new viscosity model, instead of improving the reigning model, it may lead to the first model in a new class of models. This article will display one or two representative models for different classes of viscosity models, and these classes are:
Cubic equations of state are a specific class of thermodynamic models for modeling the pressure of a gas as a function of temperature and density and which can be rewritten as a cubic function of the molar volume.