In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.

A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle.
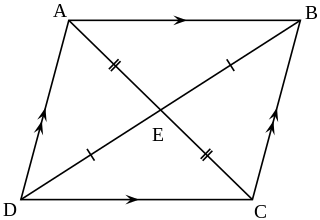
In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

In geometry, a trapezoid in North American English, or trapezium in British English, is a quadrilateral that has at least one pair of parallel sides.

In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.

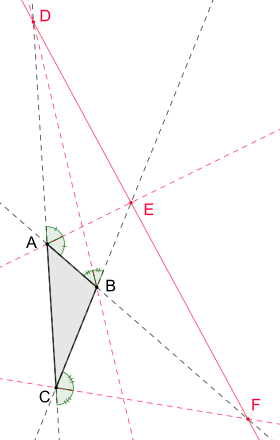
In geometry, symmedians are three particular lines associated with every triangle. They are constructed by taking a median of the triangle, and reflecting the line over the corresponding angle bisector. The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector.

In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of equal measure, or as a trapezoid whose diagonals have equal length. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides are parallel, and the two other sides are of equal length, and the diagonals have equal length. The base angles of an isosceles trapezoid are equal in measure.
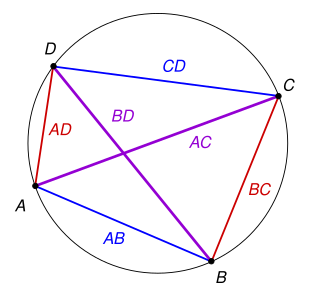
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.
In geometry, a cevian is a line segment which joins a vertex of a triangle to a point on the opposite side of the triangle. Medians and angle bisectors are special cases of cevians. The name "cevian" comes from the Italian mathematician Giovanni Ceva, who proved a well-known theorem about cevians which also bears his name.
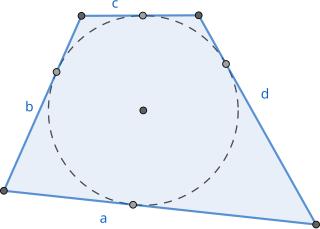
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all can be tangent to a single circle within the quadrilateral. This circle is called the incircle of the quadrilateral or its inscribed circle, its center is the incenter and its radius is called the inradius. Since these quadrilaterals can be drawn surrounding or circumscribing their incircles, they have also been called circumscribable quadrilaterals, circumscribing quadrilaterals, and circumscriptible quadrilaterals. Tangential quadrilaterals are a special case of tangential polygons.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:
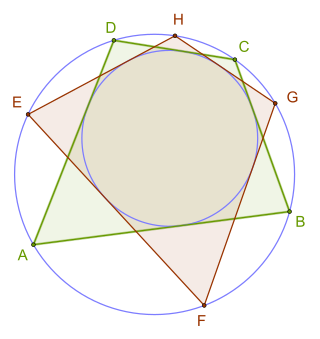
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. The radii and centers of these circles are called inradius and circumradius, and incenter and circumcenter respectively. From the definition it follows that bicentric quadrilaterals have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names for these quadrilaterals are chord-tangent quadrilateral and inscribed and circumscribed quadrilateral. It has also rarely been called a double circle quadrilateral and double scribed quadrilateral.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

In Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the extensions of all four sides are tangent to a circle outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle, its radius the exradius and its center the excenter. The excenter lies at the intersection of six angle bisectors. These are the internal angle bisectors at two opposite vertex angles, the external angle bisectors at the other two vertex angles, and the external angle bisectors at the angles formed where the extensions of opposite sides intersect. The ex-tangential quadrilateral is closely related to the tangential quadrilateral.
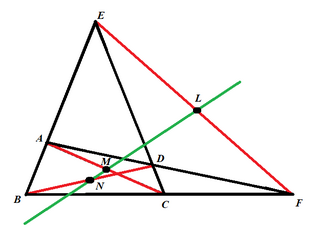
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrilateral.
![The theorem states for any triangle [?] DAB and [?] DAC where AD is a bisector, then
|
B
D
|
:
|
C
D
|
=
|
A
B
|
:
|
A
C
|
.
{\displaystyle |BD|:|CD|=|AB|:|AC|.} Triangle ABC with bisector AD.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d1/Triangle_ABC_with_bisector_AD.svg/240px-Triangle_ABC_with_bisector_AD.svg.png)



























![a
=
[?]
B
A
C
2
=
[?]
B
A
D
=
[?]
C
A
D
{\textstyle \alpha ={\frac {\angle BAC}{2}}=\angle BAD=\angle CAD} Angle bisector proof.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/4/40/Angle_bisector_proof.svg/330px-Angle_bisector_proof.svg.png)