A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius.

In geometry and algebra, a real number is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots.

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .

In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

In geometry, two geometric objects are perpendicular if their intersection forms right angles at the point of intersection called a foot. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. Perpendicular intersections can happen between two lines, between a line and a plane, and between two planes.

Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.

In geometry, bisection is the division of something into two equal or congruent parts. Usually it involves a bisecting line, also called a bisector. The most often considered types of bisectors are the segment bisector, a line that passes through the midpoint of a given segment, and the angle bisector, a line that passes through the apex of an angle . In three-dimensional space, bisection is usually done by a bisecting plane, also called the bisector.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
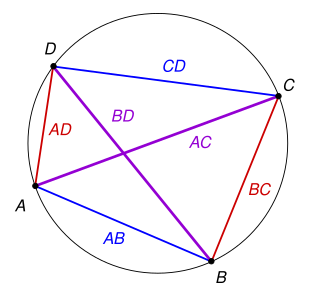
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.
In geometry, a quadratrix is a curve having ordinates which are a measure of the area of another curve. The two most famous curves of this class are those of Dinostratus and E. W. Tschirnhaus, which are both related to the circle.
In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle with ruler and compass and this curve as an additional tool. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of construction. There is a variety of such curves and the methods used to construct an angle trisector differ according to the curve. Examples include:
Dinostratus was a Greek mathematician and geometer, and the brother of Menaechmus. He is known for using the quadratrix to solve the problem of squaring the circle.

In geometry, the Steiner inellipse, midpoint inellipse, or midpoint ellipse of a triangle is the unique ellipse inscribed in the triangle and tangent to the sides at their midpoints. It is an example of an inellipse. By comparison the inscribed circle and Mandart inellipse of a triangle are other inconics that are tangent to the sides, but not at the midpoints unless the triangle is equilateral. The Steiner inellipse is attributed by Dörrie to Jakob Steiner, and a proof of its uniqueness is given by Dan Kalman.

In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin.
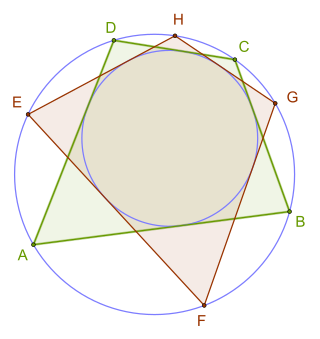
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. The radii and centers of these circles are called inradius and circumradius, and incenter and circumcenter respectively. From the definition it follows that bicentric quadrilaterals have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names for these quadrilaterals are chord-tangent quadrilateral and inscribed and circumscribed quadrilateral. It has also rarely been called a double circle quadrilateral and double scribed quadrilateral.
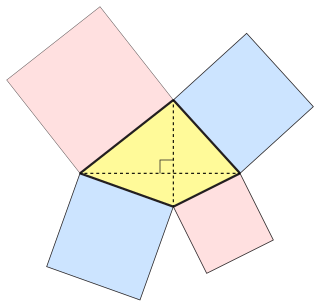
In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal (perpendicular) to each other.

In geometry, Dinostratus' theorem describes a property of Hippias' trisectrix, that allows for the squaring the circle if the trisectrix can be used in addition to straightedge and compass. The theorem is named after the Greek mathematician Dinostratus who proved it around 350 BC when he attempted to square the circle himself.

In Euclidean geometry, a tangential trapezoid, also called a circumscribed trapezoid, is a trapezoid whose four sides are all tangent to a circle within the trapezoid: the incircle or inscribed circle. It is the special case of a tangential quadrilateral in which at least one pair of opposite sides are parallel. As for other trapezoids, the parallel sides are called the bases and the other two sides the legs. The legs can be equal, but they don't have to be.
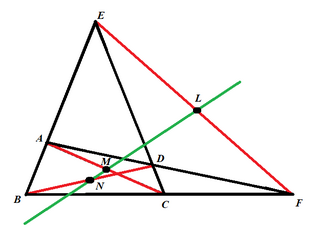
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrilateral.