In physics, the cross section is a measure of the probability that a specific process will take place when some kind of radiant excitation intersects a localized phenomenon. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

Diffraction is the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a secondary source of the propagating wave. Italian scientist Francesco Maria Grimaldi coined the word diffraction and was the first to record accurate observations of the phenomenon in 1660.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form
Fourier optics is the study of classical optics using Fourier transforms (FTs), in which the waveform being considered is regarded as made up of a combination, or superposition, of plane waves. It has some parallels to the Huygens–Fresnel principle, in which the wavefront is regarded as being made up of a combination of spherical wavefronts whose sum is the wavefront being studied. A key difference is that Fourier optics considers the plane waves to be natural modes of the propagation medium, as opposed to Huygens–Fresnel, where the spherical waves originate in the physical medium.

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.

In mathematics, the Clausen function, introduced by Thomas Clausen (1832), is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.

In physics, a wave packet is a short burst of localized wave action that travels as a unit, outlined by an envelope. A wave packet can be analyzed into, or can be synthesized from, a potentially-infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Any signal of a limited width in time or space requires many frequency components around a center frequency within a bandwidth inversely proportional to that width; even a gaussian function is considered a wave packet because its Fourier transform is a "packet" of waves of frequencies clustered around a central frequency. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant or it may change (dispersion) while propagating.

In mathematics, physics and engineering, the sinc function, denoted by sinc(x), has two forms, normalized and unnormalized.
In quantum physics, the scattering amplitude is the probability amplitude of the outgoing spherical wave relative to the incoming plane wave in a stationary-state scattering process. At large distances from the centrally symmetric scattering center, the plane wave is described by the wavefunction
Generally in scattering theory and in particular in quantum mechanics, the Born approximation consists of taking the incident field in place of the total field as the driving field at each point in the scatterer. The Born approximation is named after Max Born who proposed this approximation in early days of quantum theory development.
In mathematics, in the area of complex analysis, Nachbin's theorem is commonly used to establish a bound on the growth rates for an analytic function. This article provides a brief review of growth rates, including the idea of a function of exponential type. Classification of growth rates based on type help provide a finer tool than big O or Landau notation, since a number of theorems about the analytic structure of the bounded function and its integral transforms can be stated. In particular, Nachbin's theorem may be used to give the domain of convergence of the generalized Borel transform, given below.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
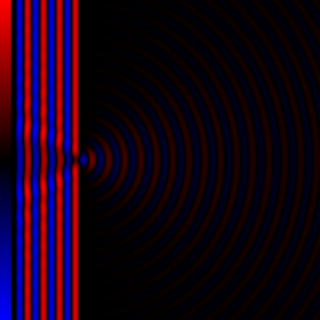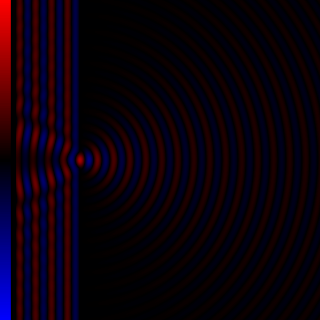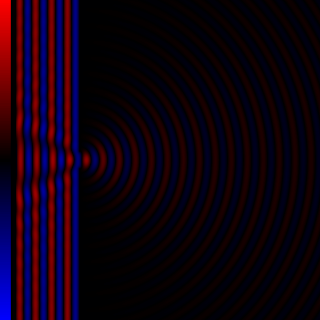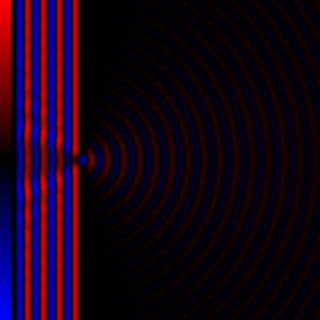
Diffraction processes affecting waves are amenable to quantitative description and analysis. Such treatments are applied to a wave passing through one or more slits whose width is specified as a proportion of the wavelength. Numerical approximations may be used, including the Fresnel and Fraunhofer approximations.
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.
Partial-wave analysis, in the context of quantum mechanics, refers to a technique for solving scattering problems by decomposing each wave into its constituent angular-momentum components and solving using boundary conditions.
In the science of fluid flow, Stokes' paradox is the phenomenon that there can be no creeping flow of a fluid around a disk in two dimensions; or, equivalently, the fact there is no non-trivial steady-state solution for the Stokes equations around an infinitely long cylinder. This is opposed to the 3-dimensional case, where Stokes' method provides a solution to the problem of flow around a sphere.









































