Potential theory of Polanyi

Last updated May 25, 2024

The potential theory of Polanyi, also called Polanyi adsorption potential theory, is a model of adsorption proposed by Michael Polanyi where adsorption can be measured through the equilibrium between the chemical potential of a gas near the surface and the chemical potential of the gas from a large distance away. In this model, he assumed that the attraction largely due to Van Der Waals forces of the gas to the surface is determined by the position of the gas particle from the surface, and that the gas behaves as an ideal gas until condensation where the gas exceeds its equilibrium vapor pressure. While the adsorption theory of Henry is more applicable in low pressure and BET adsorption isotherm equation is more useful at from 0.05 to 0.35 P/Po, the Polanyi potential theory has much more application at higher P/Po (~0.1–0.8).

Overview

Michael Polanyi

Michael Polanyi, FRS (11 March 1891 – 22 February 1976) was a Hungarian polymath, who made theoretical contribution to physical chemistry, economics, and philosophy. Polanyi was a well known theoretical chemist who contributed to the chemistry field through three main areas of study: adsorption of gases on solids, x-ray structure analysis of the properties of solids, and the rate of chemical reactions. However, Polanyi was active in both theoretical and experimental studies within the Chemistry field. Polanyi obtained a degree in medicine in 1913 as well as a Ph.D. in physical chemistry in 1917 from the University of Budapest. Later in his life, he taught as a chemistry professor at the Kaiser Wilhelm Institute in Berlin as well as the University of Manchester in Manchester, England.

History

Proposed theory

In 1914, Polanyi wrote his first paper proposed on adsorption where he proposed a model for the adsorption of gas onto a solid surface.^[1] Afterwards, he published a fully developed paper in 1916, which included experimental verification by his students and other authors. During his research in the University of Budapest, his mentor, Professor Georg Bredig, sent his research findings to Albert Einstein. Einstein wrote back to Bredig stating:

The papers of your M. Polanyi please me a lot. I have checked over the essentials in them and found them fundamentally correct.

Polanyi later described this event by saying:

Bang! I was a scientist.

Polanyi and Einstein continued to write to each other on and off for the next 20 years.

Criticism

Polanyi's model of adsorption was met with much criticism for several decades after publication years. His simplistic model for determining adsorption was formed during the time of the discovery of Debye's fixed dipoles, Bohr's atomic model, and well as the developing theory of intermolecular forces and electrostatic forces by key figures in the chemistry world including W.H. Bragg, W.L. Bragg, and Willem Hendrik Keesom. Opponents of his model claimed that Polanyi's theory did not take into account these emerging theories. Criticism included that the model did not take into account the electrical interactions of the gas and the surface, and that the presence of other molecules would screen off the attraction of the gas to the surface. Polanyi's model was furthermore put under scrutiny following the experimental claims of Irving Langmuir from 1916 to 1918 through whose research would eventually win the Nobel Prize in 1932. However, Polanyi was not able to participate in many of these discussions because he served as a medical officer for the Austro-Hungarian army in the Serbian front during World War I. Polanyi wrote about this experience saying:

I myself was protected for a while against any knowledge of these developments by serving as a medical officer in the Austro-Hungarian Army from August 1914 to October 1918, and by the subsequent revolutions and counter revolutions that lasted until the end of 1919. Members of less-well-informed circles elsewhere continued to be impressed for some time by the simplicity of my theory and its wide experimental verifications.^[1]

Defense

Polanyi described that the “turning point” of the acceptance of his model of adsorption occurred when Fritz Haber asked him to defend his theory in full in the Kaiser Wilhelm Institute for Physical Chemistry in Berlin, Germany. Many key players in the scientific world were present in this meeting including Albert Einstein. After hearing Polanyi's full explanation of his model, Haber and Einstein claimed that Polanyi “had displayed a total disregard for the scientifically established structure of the matter”. Years later, Polanyi described his ordeal by concluding,

Professionally, I survived the occasion only by the skin of my teeth.

Polanyi continued to provide supporting evidence in proving the validity of his model years after this meeting.^[1]

Refutation

Polanyi's 'deliverance' (as he described it) from these rejections and criticism of his model occurred in 1930, when Fritz London proposed a new theory of cohesive forces founded on the theories of quantum mechanics on the polarization of electronic systems. Polanyi wrote to London asking,

“Are these forces subject to screening by intervening molecules? Would a solid acting by these forces possess a spatially fixed adsorption potential?”

After computational analysis, a joint publication was made between Polanyi and London claiming that the adsorptive forces behaved similarly to the model that Polanyi had proposed.^[1]

Further research

Polanyi's theory has historical significance whose work has been used a foundation for other models, such as the theory of volume filling micropores (TVFM) and the Dubinin–Radushkevich theory. Other research have been performed loosely involving the potential theory of Polanyi such as the capillary condensation phenomenon discovered by Zsigmondy. Unlike Poylani's theory which involves a flat surface, Zsigmondy's research involves a porous structure like silica materials. His research proved that condensation of vapors can occur in narrow pores below the standard saturated vapour pressure.^[2]

Theory

Polanyi potential adsorption theory

The Polanyi potential adsorption theory is based on the assumption that the molecules near a surface move according to a potential, similar to that of gravity or electric fields.^[3] This model is applicable in the case of gases at a surface at constant temperature. Gas molecules move closer to that surface when the pressure is higher than the equilibrium vapor pressure. The change in potential relative to the distance from the surface can be calculated using the formula for difference of the chemical potential,

\mathrm {d} \mu =-S_{\rm {m}}\,\mathrm {d} T+V_{\rm {m}}\,\mathrm {d} p+\mathrm {d} U_{\rm {m}}

where $\mu$ is the chemical potential, $S_{\rm {m}}$ is the molar entropy, $V_{\rm {m}}$ is the molar volume, and $U_{\rm {m}}$ is the molar internal energy.

At equilibrium, the chemical potential of a gas at a distance $r$ from a surface, ${\mu (r,p_{r})}$ , is equal to the chemical potential of the gas at an infinitely large distance from the surface, ${\mu (\infty ,p)}$ . As a result, the integration from an infinitely far distance to r distance from the surface leads to

\int _{\mu (\infty ,p)}^{\mu (r,p_{r})}\mathrm {d} \mu ={\mu (r,P_{r})}-{\mu (\infty ,p)}=0

where $p_{r}$ is the partial pressure at distance r and $p$ is the partial pressure at infinite distance from the surface.

Since the temperature remains constant, the difference in chemical potential formula can be integrated over pressures $p$ and $p_{r}$

\int _{p}^{p_{r}}V_{\rm {m}}\,\mathrm {d} P+U_{\rm {m}}(r)-U_{\rm {m}}(\infty )=0

By setting the $U_{\rm {m}}(\infty )=0$ , the equation can be simplified to

-U_{\rm {m}}(r)=\int _{p}^{p_{r}}V_{\rm {m}}\,\mathrm {d} p

Using the ideal gas law, $pV_{\rm {m}}=RT$ , the following formula is obtained

-U_{\rm {m}}(r)=\int _{p}^{p_{r}}{\frac {RT}{p}}\mathrm {d} p=RT\ln {\frac {p_{r}}{p}}

Since gas condenses into a liquid on a surface when the pressure of the gas exceeds the equilibrium vapor pressure, $p_{0}$ , we can assume a liquid film forms over the surface of thickness, $\delta$ . The energy at $p_{0}$ is

U_{\rm {m}}(\delta )=-RT\ln {\frac {p_{0}}{p}}

Considering that the partial pressure of the gases relates to the concentration, the adsorption potential, $\varepsilon _{\rm {s}}$ can be calculated as

\varepsilon _{s}=-RT\ln {\frac {c_{\rm {s}}}{c}}

where $c_{\rm {s}}$ is the saturated concentration of adsorbate and $c$ is the equilibrium concentration of the adsorbate.

Theories based on Polanyi adsorption theory

The potential theory underwent many refinements and changes throughout the years since its first report. One major theories of note that was developed using Polanyi's theory was the Dubinin theories, Dubinin–Radushkivech and Dubinin–Astakhov equations.

Using the adsorption potential, the degree of filling of the adsorption space, $\theta$ , can be calculated as

\theta =a/a_{0}=\mathrm {e} ^{{({A/E})}^{b}}

where $a$ is value of adsorption at temperature T and equilibrium pressure p, $a_{0}$ is the maximum value of adsorption, and $E$ is the characteristic energy of adsorption in kJ/mol, $A$ is the loss in Gibbs free energy in adsorption equal to $\Delta G=-RT\log(p_{0}/p)$ and $b$ is the fitting coefficient.^[4] The Dubinin–Radushkivech equation where $b$ is equal to 2 and the optimized Dubinin-Astakhov equation where $b$ is fit to experimental data can be simplified to

\log a=\log a_{0}+0.434\left({\frac {A}{E}}\right)^{b}

Changes in Dubinin-Astakhov curves due to increases in Q , E, and b on a log-log scale plot of solute isotherms on a sorbent versus relative solute concentration.
Top-left: Q = 60; b = 1
Top-right: Q = 60; b = 1.5
Bottom-left: Q = 60; E = 20
Bottom-right: E = 20; b = 1.5 Dubinin-Astakhov Curves.png — Changes in Dubinin–Astakhov curves due to increases in Q , E, and b on a log-log scale plot of solute isotherms on a sorbent versus relative solute concentration.
Top-left: Q = 60; b = 1
Top-right: Q = 60; b = 1.5
Bottom-left: Q = 60; E = 20
Bottom-right: E = 20; b = 1.5

Other studies have used the Dubinin–Astakhov in a similar form of $\log q_{\rm {e}}=\log Q^{0}+(\varepsilon _{\rm {sw}}/E)^{b}$ ,

where $q_{\rm {e}}$ is equilibrium adsorbed concentration of adsorbent in mg/g, $Q^{0}$ is maximum adsorbed concentration of adsorbent in mg/g, $\varepsilon _{\rm {sw}}$ is the effective adsorption potential, where equal to $\varepsilon _{\rm {sw}}=-RT\ln(c_{\rm {e}}/c_{\rm {s}})$ , $c_{\rm {e}}$ is equilibrium concentration of adsorbent in the solution phase in mg/L, and $c_{\rm {s}}$ is the adsorbent solubility in water in mg/L.^[5]

The characteristic energy of adsorption can be related to a characteristic energy of adsorption for a standard vapor on the same surface, $E_{0}$ , through the use of an affinity coefficient, $\beta$

E=\beta E_{0}

The affinity coefficient is a ratio of the properties of the sample and standard vapors

\beta ={\frac {\alpha }{\alpha _{0}}}

where $\alpha$ and $\alpha _{0}$ are the polarizabilities of the sample and standard vapors, respectively. Many studies have been performed to determine optimal fitting coefficients, $b$ , and affinity coefficients, $\beta$ , to best describe the adsorption of gases and vapors onto solids. As a result, the Dubinin–Astakhov equation remains in use in adsorption studies due to the accuracy it can obtain when fitted with experimental results.

Dubinin–Astakhov parameters for vapors and gases

Compound	Activated carbon	$b$	$\beta E$ , kJ/mol	$\beta$	Source
Benzene	Carbon molecular sieve	1.78	11.52	1.00	^[6]
Acetone	Carbon molecular sieve	2.00	9.774	0.85	^[6]
Benzene	CAL AC	2	18.23	1.00	^[7]
Acetone	CAL AC	2	13.21	0.72	^[7]
Acetone	Carbon molecular sieve	2.8	20.29	0.72	^[8]
Benzene	Carbon molecular sieve	3.1	28.87	1.00	^[8]
Nitrogen	Carbon molecular sieve	2.6	11.72	0.41	^[8]
Oxygen	Carbon molecular sieve	2.3	9.21	0.32	^[8]
Hydrogen	Carbon molecular sieve	2.5	5.44	0.19	^[8]

Application

In many modern studies, the Polanyi theory is widely used in the study of activated carbons, or carbon black. The theory has been successfully used to model a variety of scenarios such as the gas adsorption on activated carbon and the adsorption process of nonionic polycyclic aromatic hydrocarbons.^[9] Later on, experiments also showed that it can model ionic polycyclic aromatic hydrocarbons such as phenols and anilines. More recently, the Polyani adsorption isotherm has been used to model to adsorption of carbon nanoparticles.

Characterization of carbon nanoparticles

Historically, the theory was used to model nonuniform adsorbates and multi-components solutes. For certain pairs of adsorbates and adsorbents, the mathematical parameters of the Polyani theory can be related to the physicochemical properties of both adsorbents and adsorbates. The theory has been used to model the adsorption of carbon nanotubes and carbon nanoparticles. In the study done by Yang and Xing,^[5] the theory have been shown to better fit the adsorption isotherm than Langmuir, Freundlich, and partition. The experiment studied the adsorption of organic molecules on carbon nanoparticles and carbon nanotubes. According to the Polyani theory the surface defect curvatures of carbon nanoparticles could affect their adsorption. Flat surfaces on the particles will allow more surface atoms to approach adsorbing organic molecules which will increase the potential, leading to stronger interactions. The theory has been beneficial in trying to understand the adsorption mechanisms of organic compounds on carbon nanoparticles and estimating the adsorption capacity and affinity. Using this theory, researchers are hoping to be able to design carbon nanoparticles for specific needs such as using them as sorbents in environmental studies.

Adsorption from different systems

In one of the earlier studies conducted by Manes, M., & Hofer, L. J. E.,^[10] the Polyani theory was used to characterize liquid-phase adsorption isotherms on various concentrations activated carbon using a wide range of organic solvent. The polyani theory was shown to be a good fit for these various systems. Because of the results, the study introduced the possibility of predicting isotherms for similar systems using minimal data. However, the limitation is that the adsorption isotherms for a large variety of solvents can only fit over a limited range. The curve was not able to fit the data at high-capacity range. The study also concluded that there were a few anomalies in the results. The adsorption from carbon tetrachloride, cyclohexane, and carbon disulfide onto activated carbon was not able to fit well to the curve, and remain to be explained. The researchers who conducted the experiment speculate that steric effects of carbon tetrachloride and cyclohexane may have played a role. The study has been done with a variety of systems such as organic liquids from water solutions and organic solids from water solutions.

Competitive adsorption

Since a variety of systems have been investigated, a study was done to investigate the individual adsorption of a mixed solution. This phenomenon is also called competitive adsorption because solutes tend to compete for the same adsorption sites. In the experiment conducted by Rosene and Manes,^[11] the competitive adsorption of glucose, urea, benzoic acid, phthalide, and p-nitrophenol. Using the Polanyi adsorption model, they were able to calculate the relative adsorption of each compound onto the surface of activated carbon.

Related Research Articles

In a chemical reaction, chemical equilibrium is the state in which both the reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.

<span class="mw-page-title-main">Fermi gas</span> Physical model of gases composed of many non-interacting identical fermions

A Fermi gas is an idealized model, an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi.

Adsorption is the adhesion of atoms, ions or molecules from a gas, liquid or dissolved solid to a surface. This process creates a film of the adsorbate on the surface of the adsorbent. This process differs from absorption, in which a fluid is dissolved by or permeates a liquid or solid. While adsorption does often precede absorption, which involves the transfer of the absorbate into the volume of the absorbent material, alternatively, adsorption is distinctly a surface phenomenon, wherein the adsorbate does not penetrate through the material surface and into the bulk of the adsorbent. The term sorption encompasses both adsorption and absorption, and desorption is the reverse of sorption.

In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, the chemical potential of any chemical species is uniformly the same everywhere throughout the system.

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as

In physical chemistry, Henry's law is a gas law that states that the amount of dissolved gas in a liquid is directly proportional to its partial pressure above the liquid. The proportionality factor is called Henry's law constant. It was formulated by the English chemist William Henry, who studied the topic in the early 19th century. In simple words, we can say that the partial pressure of a gas in vapour phase is directly proportional to the mole fraction of a gas in solution.

In chemistry, an ideal solution or ideal mixture is a solution that exhibits thermodynamic properties analogous to those of a mixture of ideal gases. The enthalpy of mixing is zero as is the volume change on mixing by definition; the closer to zero the enthalpy of mixing is, the more "ideal" the behavior of the solution becomes. The vapor pressures of the solvent and solute obey Raoult's law and Henry's law, respectively, and the activity coefficient is equal to one for each component.

The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.

In chemical thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of chemical equilibrium. It is equal to the pressure of an ideal gas which has the same temperature and molar Gibbs free energy as the real gas.

In thermodynamics, an activity coefficient is a factor used to account for deviation of a mixture of chemical substances from ideal behaviour. In an ideal mixture, the microscopic interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an activity coefficient. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient.

Desorption is the physical process where adsorbed atoms or molecules are released from a surface into the surrounding vacuum or fluid. This occurs when a molecule gains enough energy to overcome the activation barrier and the binding energy that keep it attached to the surface.

Brunauer–Emmett–Teller (BET) theory aims to explain the physical adsorption of gas molecules on a solid surface and serves as the basis for an important analysis technique for the measurement of the specific surface area of materials. The observations are very often referred to as physical adsorption or physisorption. In 1938, Stephen Brunauer, Paul Hugh Emmett, and Edward Teller presented their theory in the Journal of the American Chemical Society. BET theory applies to systems of multilayer adsorption that usually utilizes a probing gas (called the adsorbate) that does not react chemically with the adsorptive (the material upon which the gas attaches to) to quantify specific surface area. Nitrogen is the most commonly employed gaseous adsorbate for probing surface(s). For this reason, standard BET analysis is most often conducted at the boiling temperature of N₂ (77 K). Other probing adsorbates are also utilized, albeit less often, allowing the measurement of surface area at different temperatures and measurement scales. These include argon, carbon dioxide, and water. Specific surface area is a scale-dependent property, with no single true value of specific surface area definable, and thus quantities of specific surface area determined through BET theory may depend on the adsorbate molecule utilized and its adsorption cross section.

The Gibbs adsorption isotherm for multicomponent systems is an equation used to relate the changes in concentration of a component in contact with a surface with changes in the surface tension, which results in a corresponding change in surface energy. For a binary system, the Gibbs adsorption equation in terms of surface excess is

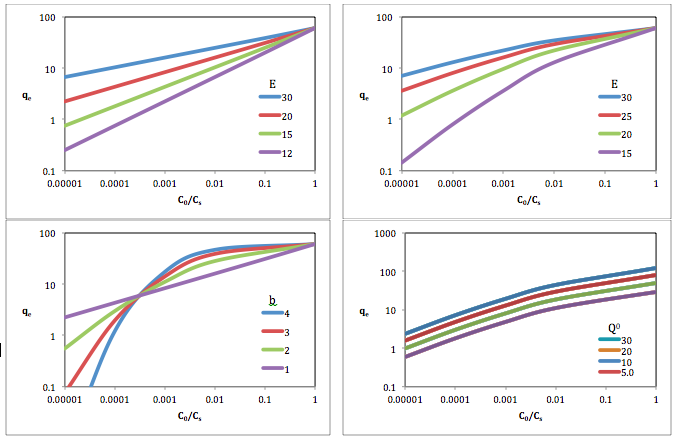
The Freundlich equation or Freundlich adsorption isotherm, an adsorption isotherm, is an empirical relationship between the quantity of a gas adsorbed into a solid surface and the gas pressure. The same relationship is also applicable for the concentration of a solute adsorbed onto the surface of a solid and the concentration of the solute in the liquid phase. In 1909, Herbert Freundlich gave an expression representing the isothermal variation of adsorption of a quantity of gas adsorbed by unit mass of solid adsorbent with gas pressure. This equation is known as Freundlich adsorption isotherm or Freundlich adsorption equation. As this relationship is entirely empirical, in the case where adsorption behavior can be properly fit by isotherms with a theoretical basis, it is usually appropriate to use such isotherms instead. The Freundlich equation is also derived (non-empirically) by attributing the change in the equilibrium constant of the binding process to the heterogeneity of the surface and the variation in the heat of adsorption.

In materials science, segregation is the enrichment of atoms, ions, or molecules at a microscopic region in a materials system. While the terms segregation and adsorption are essentially synonymous, in practice, segregation is often used to describe the partitioning of molecular constituents to defects from solid solutions, whereas adsorption is generally used to describe such partitioning from liquids and gases to surfaces. The molecular-level segregation discussed in this article is distinct from other types of materials phenomena that are often called segregation, such as particle segregation in granular materials, and phase separation or precipitation, wherein molecules are segregated in to macroscopic regions of different compositions. Segregation has many practical consequences, ranging from the formation of soap bubbles, to microstructural engineering in materials science, to the stabilization of colloidal suspensions.

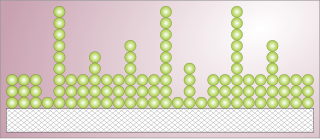
The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressure i.e. at these conditions the adsorbate's partial pressure $is related to its volume V adsorbed onto a solid adsorbent. The adsorbent, as indicated in the figure, is assumed to be an ideal solid surface composed of a series of distinct sites capable of binding the adsorbate. The adsorbate binding is treated as a chemical reaction between the adsorbate gaseous molecule and an empty sorption site S . This reaction yields an adsorbed species with an associated equilibrium constant :$

Supercritical adsorption also referred to as the adsorption of supercritical fluids, is the adsorption at above-critical temperatures. There are different tacit understandings of supercritical fluids. For example, “a fluid is considered to be ‘supercritical’ when its temperature and pressure exceed the temperature and pressure at the critical point”. In the studies of supercritical extraction, however, “supercritical fluid” is applied for a narrow temperature region of 1-1.2 $or to +10 K, which is called the supercritical region.$

Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordinate is zero. This principle, applied to mixtures at equilibrium provides a definition of an equilibrium constant. Applications include acid–base, host–guest, metal–complex, solubility, partition, chromatography and redox equilibria.

Adsorption is the adhesion of ions or molecules onto the surface of another phase. Adsorption may occur via physisorption and chemisorption. Ions and molecules can adsorb to many types of surfaces including polymer surfaces. A polymer is a large molecule composed of repeating subunits bound together by covalent bonds. In dilute solution, polymers form globule structures. When a polymer adsorbs to a surface that it interacts favorably with, the globule is essentially squashed, and the polymer has a pancake structure.

References

1 2 3 4 Polanyi, M (1963). "The Potential Theory of Adsorption". Science. 141 (3585): 1010–013. Bibcode:1963Sci...141.1010P. doi:10.1126/science.141.3585.1010. PMID 17739484.
↑ Dabrowski, A. (2001). "Adsorption from theory to practice" (PDF). Advances in Colloid and Interface Science. 93: 135–224.
↑ Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2003). Physics and Chemistry of Interfaces. pp. 193–195. doi:10.1002/3527602313. ISBN 978-3-527-40413-1.
↑ Dubinin, M. M.; Astakhov, V. A. (1971). "Development of the Concepts of Volume Filling of Micropores in the Adsorption of Gases and Vapors by Microporous Adsorbents". Bulletin of the Academy of Sciences of the USSR, Division of Chemical Science. 20 (1): 3–7. doi:10.1007/bf00849307.
1 2 Yang, K.; Xing, B. (2010). "Adsorption of organic compounds by carbon nanomaterials in aqueous phase: Polanyi theory and its application". Chemical Reviews. 110 (10): 5989–6008. doi:10.1021/cr100059s. PMID 20518459.
1 2 Doong, S. J.; Yang, R. T. (1988). "A simple potential theory model for predicting mixed-gas adsorption". Industrial & Engineering Chemistry Research. 27 (4): 630–635. doi:10.1021/ie00076a017.
1 2 Tamon, H.; Okazaki, M. (1996). "Influence of acidic surface oxides of activated carbon on gas adsorption characteristics". Carbon. 34 (6): 741–746. doi:10.1016/0008-6223(96)00029-2.
1 2 3 4 5 Kawazoe, K.; Kawai, T.; Eguchi, Y.; Itoga, K. (1974). "Correlation of adsorption equilibrium data of various gases and vapors on molecular-sieving carbon". Journal of Chemical Engineering of Japan. 7 (3): 158–162. doi: 10.1252/jcej.7.158 .
↑ Yang, K.; Wu, W.; Jing, Q & Zhu, L. (2008). "Aqueous adsorption of aniline, phenol, and their substitutes by multi-walled carbon nanotubes". Environmental Science and Technology. 42 (21): 7931–6. Bibcode:2008EnST...42.7931Y. doi:10.1021/es801463v. PMID 19031883.{{cite journal}}: CS1 maint: multiple names: authors list (link)
↑ Manes, M.; Hofer, B.J.E. (1969). "Application of the Polanyi adsorption potential theory to adsorption from solution on activated carbon". The Journal of Physical Chemistry. 73 (3): 584–590. doi:10.1021/j100723a018.
↑ Manes, M.R.; Manes, M. (1976). "Application of the Polanyi adsorption potential theory to adsorption from solution on activated carbon. VII. Competitive adsorption of solids from water solution". The Journal of Physical Chemistry. 80 (9): 953–959. doi:10.1021/j100550a007.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[polanyi-1] 1 2 3 4 Polanyi, M (1963). "The Potential Theory of Adsorption". Science. 141 (3585): 1010–013. Bibcode:1963Sci...141.1010P. doi:10.1126/science.141.3585.1010. PMID 17739484.

[2] Dabrowski, A. (2001). "Adsorption from theory to practice" (PDF). Advances in Colloid and Interface Science. 93: 135–224.

[Physics_and_Chemistry_of_Interfaces-3] Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2003). Physics and Chemistry of Interfaces. pp. 193–195. doi:10.1002/3527602313. ISBN 978-3-527-40413-1.

[4] Dubinin, M. M.; Astakhov, V. A. (1971). "Development of the Concepts of Volume Filling of Micropores in the Adsorption of Gases and Vapors by Microporous Adsorbents". Bulletin of the Academy of Sciences of the USSR, Division of Chemical Science. 20 (1): 3–7. doi:10.1007/bf00849307.

[Xing-5] 1 2 Yang, K.; Xing, B. (2010). "Adsorption of organic compounds by carbon nanomaterials in aqueous phase: Polanyi theory and its application". Chemical Reviews. 110 (10): 5989–6008. doi:10.1021/cr100059s. PMID 20518459.

[Doong-6] 1 2 Doong, S. J.; Yang, R. T. (1988). "A simple potential theory model for predicting mixed-gas adsorption". Industrial & Engineering Chemistry Research. 27 (4): 630–635. doi:10.1021/ie00076a017.

[Tamon-7] 1 2 Tamon, H.; Okazaki, M. (1996). "Influence of acidic surface oxides of activated carbon on gas adsorption characteristics". Carbon. 34 (6): 741–746. doi:10.1016/0008-6223(96)00029-2.

[Kawazoe-8] 1 2 3 4 5 Kawazoe, K.; Kawai, T.; Eguchi, Y.; Itoga, K. (1974). "Correlation of adsorption equilibrium data of various gases and vapors on molecular-sieving carbon". Journal of Chemical Engineering of Japan. 7 (3): 158–162. doi: 10.1252/jcej.7.158 .

[9] Yang, K.; Wu, W.; Jing, Q & Zhu, L. (2008). "Aqueous adsorption of aniline, phenol, and their substitutes by multi-walled carbon nanotubes". Environmental Science and Technology. 42 (21): 7931–6. Bibcode:2008EnST...42.7931Y. doi:10.1021/es801463v. PMID 19031883.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[10] Manes, M.; Hofer, B.J.E. (1969). "Application of the Polanyi adsorption potential theory to adsorption from solution on activated carbon". The Journal of Physical Chemistry. 73 (3): 584–590. doi:10.1021/j100723a018.

[11] Manes, M.R.; Manes, M. (1976). "Application of the Polanyi adsorption potential theory to adsorption from solution on activated carbon. VII. Competitive adsorption of solids from water solution". The Journal of Physical Chemistry. 80 (9): 953–959. doi:10.1021/j100550a007.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]