 | |
| Identifiers | |
|---|---|
3D model (JSmol) | |
| ChemSpider | |
| ECHA InfoCard | 100.031.384 |
| EC Number |
|
PubChem CID | |
| |
| |
| Properties | |
| B6Sm | |
| Molar mass | 215.22 g·mol−1 |
| Melting point | 2400 °C ±100 [1] |
Except where otherwise noted, data are given for materials in their standard state (at 25 °C [77 °F], 100 kPa). | |
Samarium hexaboride (SmB6) is an intermediate-valence compound where samarium is present both as Sm2+ and Sm3+ ions at the ratio 3:7. [2] It is a Kondo insulator having a metallic surface state. [3]
It was first studied by soviet scientists in the early 1960s. [4] Further studies were then undertaken at Bell Laboratories. [4] By 1968 their researchers had noted changes in the electronic configuration at different temperatures. [5] At temperatures above 50 K its properties are typical of a Kondo metal, with metallic electrical conductivity characterized by strong electron scattering, whereas at low temperatures, it behaves as a non-magnetic insulator with a narrow band gap of about 4–14 meV. [6] The cooling-induced metal-insulator transition in SmB6 is accompanied by a sharp increase in thermal conductivity, peaking at about 15 K. The reason for this increase is that electrons do not contribute to thermal conductivity at low temperatures, which is instead dominated by phonons. The decrease in electron concentration reduced the rate of electron-phonon scattering. [7]
By the twenty first century condensed matter physicists grew more interested in SmB6 with claims that it may be a topological insulator. [8] [9] [10] Other researchers found no evidence of topological surface states. [11]
The increasing electrical resistance with a reduction in temperature indicates that the material behaves as an insulator; however, recent measurements reveal a Fermi surface (an abstract boundary of electrons in momentum space) characteristic of a good metal, indicating a more exotic dual metal-insulating ground state. [12] [13] The electrical resistivity at temperatures below 4K displays a distinct plateau, [14] which is thought to be the coexistence of an insulating state (bulk) and a conducting state (surface). At temperatures approaching absolute zero, the quantum oscillations of the material grow as the temperature declines, a behavior that contradicts both the Fermi analysis and the rules that govern conventional metals. [12] [15] [13] While it has been argued that quantum oscillations on samples grown from aluminium flux [16] may arise from aluminum inclusions, [17] such an explanation is excluded for samples grown by the image furnace method [12] [14] rather than by the flux growth method. [16] [17]
Samarium is a chemical element; it has symbol Sm and atomic number 62. It is a moderately hard silvery metal that slowly oxidizes in air. Being a typical member of the lanthanide series, samarium usually has the oxidation state +3. Compounds of samarium(II) are also known, most notably the monoxide SmO, monochalcogenides SmS, SmSe and SmTe, as well as samarium(II) iodide.
In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change i.e. a minimum in electrical resistivity with temperature. The cause of the effect was first explained by Jun Kondo, who applied third-order perturbation theory to the problem to account for scattering of s-orbital conduction electrons off d-orbital electrons localized at impurities. Kondo's calculation predicted that the scattering rate and the resulting part of the resistivity should increase logarithmically as the temperature approaches 0 K. Experiments in the 1960s by Myriam Sarachik at Bell Laboratories provided the first data that confirmed the Kondo effect. Extended to a lattice of magnetic impurities, the Kondo effect likely explains the formation of heavy fermions and Kondo insulators in intermetallic compounds, especially those involving rare earth elements such as cerium, praseodymium, and ytterbium, and actinide elements such as uranium. The Kondo effect has also been observed in quantum dot systems.
In physics, topological order is a kind of order in the zero-temperature phase of matter. Macroscopically, topological order is defined and described by robust ground state degeneracy and quantized non-Abelian geometric phases of degenerate ground states. Microscopically, topological orders correspond to patterns of long-range quantum entanglement. States with different topological orders cannot change into each other without a phase transition.
In condensed matter physics, a pseudogap describes a state where the Fermi surface of a material possesses a partial energy gap, for example, a band structure state where the Fermi surface is gapped only at certain points.
A charge density wave (CDW) is an ordered quantum fluid of electrons in a linear chain compound or layered crystal. The electrons within a CDW form a standing wave pattern and sometimes collectively carry an electric current. The electrons in such a CDW, like those in a superconductor, can flow through a linear chain compound en masse, in a highly correlated fashion. Unlike a superconductor, however, the electric CDW current often flows in a jerky fashion, much like water dripping from a faucet due to its electrostatic properties. In a CDW, the combined effects of pinning and electrostatic interactions likely play critical roles in the CDW current's jerky behavior, as discussed in sections 4 & 5 below.
In solid-state physics, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons in unfilled electron bands. Electrons are one type of fermion, and when they are found in such materials, they are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free electron model. The properties of the heavy fermion compounds often derive from the partly filled f-orbitals of rare-earth or actinide ions, which behave like localized magnetic moments. The name "heavy fermion" comes from the fact that the fermion behaves as if it has an effective mass greater than its rest mass. In the case of electrons, below a characteristic temperature (typically 10 K), the conduction electrons in these metallic compounds behave as if they had an effective mass up to 1000 times the free particle mass. This large effective mass is also reflected in a large contribution to the resistivity from electron-electron scattering via the Kadowaki–Woods ratio. Heavy fermion behavior has been found in a broad variety of states including metallic, superconducting, insulating and magnetic states. Characteristic examples are CeCu6, CeAl3, CeCu2Si2, YbAl3, UBe13 and UPt3.
The quantum spin Hall state is a state of matter proposed to exist in special, two-dimensional semiconductors that have a quantized spin-Hall conductance and a vanishing charge-Hall conductance. The quantum spin Hall state of matter is the cousin of the integer quantum Hall state, and that does not require the application of a large magnetic field. The quantum spin Hall state does not break charge conservation symmetry and spin- conservation symmetry.
Subir Sachdev is Herchel Smith Professor of Physics at Harvard University specializing in condensed matter. He was elected to the U.S. National Academy of Sciences in 2014, and received the Lars Onsager Prize from the American Physical Society and the Dirac Medal from the ICTP in 2018. He was a co-editor of the Annual Review of Condensed Matter Physics from 2017–2019.
A topological insulator is a material whose interior behaves as an electrical insulator while its surface behaves as an electrical conductor, meaning that electrons can only move along the surface of the material.
In condensed matter physics, Luttinger's theorem is a result derived by J. M. Luttinger and J. C. Ward in 1960 that has broad implications in the field of electron transport. It arises frequently in theoretical models of correlated electrons, such as the high-temperature superconductors, and in photoemission, where a metal's Fermi surface can be directly observed.
In solid-state physics, Kondo insulators (also referred as Kondo semiconductors and heavy fermion semiconductors) are understood as materials with strongly correlated electrons, that open up a narrow band gap (in the order of 10 meV) at low temperatures with the chemical potential lying in the gap, whereas in heavy fermion materials the chemical potential is located in the conduction band. The band gap opens up at low temperatures due to hybridization of localized electrons (mostly f-electrons) with conduction electrons, a correlation effect known as the Kondo effect. As a consequence, a transition from metallic behavior to insulating behavior is seen in resistivity measurements. The band gap could be either direct or indirect. Most studied Kondo insulators are FeSi, Ce3Bi4Pt3, SmB6, YbB12, and CeNiSn, although there are over a dozen known Kondo insulators.
Piers Coleman is a British-born theoretical physicist, working in the field of theoretical condensed matter physics. Coleman is professor of physics at Rutgers University in New Jersey and at Royal Holloway, University of London.
Bismuth selenide is a gray compound of bismuth and selenium also known as bismuth(III) selenide.
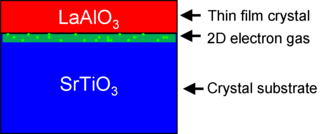
The interface between lanthanum aluminate (LaAlO3) and strontium titanate (SrTiO3) is a notable materials interface because it exhibits properties not found in its constituent materials. Individually, LaAlO3 and SrTiO3 are non-magnetic insulators, yet LaAlO3/SrTiO3 interfaces can exhibit electrical metallic conductivity, superconductivity, ferromagnetism, large negative in-plane magnetoresistance, and giant persistent photoconductivity. The study of how these properties emerge at the LaAlO3/SrTiO3 interface is a growing area of research in condensed matter physics.
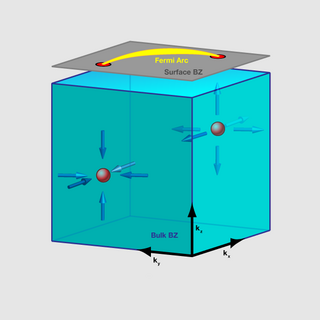
Weyl fermions are massless chiral fermions embodying the mathematical concept of a Weyl spinor. Weyl spinors in turn play an important role in quantum field theory and the Standard Model, where they are a building block for fermions in quantum field theory. Weyl spinors are a solution to the Dirac equation derived by Hermann Weyl, called the Weyl equation. For example, one-half of a charged Dirac fermion of a definite chirality is a Weyl fermion.
Dirac cones, named after Paul Dirac, are features that occur in some electronic band structures that describe unusual electron transport properties of materials like graphene and topological insulators. In these materials, at energies near the Fermi level, the valence band and conduction band take the shape of the upper and lower halves of a conical surface, meeting at what are called Dirac points.
YbBiPt is an intermetallic material which at low temperatures exhibits an extremely high value of specific heat, which is a characteristic of heavy-fermion behavior. YbBiPt has a noncentrosymmetric cubic crystal structure; in particular it belongs to the ternary half-Heusler compounds.
The term Dirac matter refers to a class of condensed matter systems which can be effectively described by the Dirac equation. Even though the Dirac equation itself was formulated for fermions, the quasi-particles present within Dirac matter can be of any statistics. As a consequence, Dirac matter can be distinguished in fermionic, bosonic or anyonic Dirac matter. Prominent examples of Dirac matter are graphene and other Dirac semimetals, topological insulators, Weyl semimetals, various high-temperature superconductors with -wave pairing and liquid helium-3. The effective theory of such systems is classified by a specific choice of the Dirac mass, the Dirac velocity, the gamma matrices and the space-time curvature. The universal treatment of the class of Dirac matter in terms of an effective theory leads to a common features with respect to the density of states, the heat capacity and impurity scattering.
Magnetic topological insulators are three dimensional magnetic materials with a non-trivial topological index protected by a symmetry other than time-reversal. In contrast with a non-magnetic topological insulator, a magnetic topological insulator can have naturally gapped surface states as long as the quantizing symmetry is broken at the surface. These gapped surfaces exhibit a topologically protected half-quantized surface anomalous Hall conductivity perpendicular to the surface. The sign of the half-quantized surface anomalous Hall conductivity depends on the specific surface termination.
Samarium compounds are compounds formed by the lanthanide metal samarium (Sm). In these compounds, samarium generally exhibits the +3 oxidation state, such as SmCl3, Sm(NO3)3 and Sm(C2O4)3. Compounds with samarium in the +2 oxidation state are also known, for example SmI2.
