
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low densities is cooled to temperatures very close to absolute zero. Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which microscopic quantum-mechanical phenomena, particularly wavefunction interference, become apparent macroscopically. More generally, condensation refers to the appearance of macroscopic occupation of one or several states: for example, in BCS theory, a superconductor is a condensate of Cooper pairs. As such, condensation can be associated with phase transition, and the macroscopic occupation of the state is the order parameter.
The quantum Hall effect is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values

Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of the conduction electrons in most metals at sufficiently low temperatures. The theory describes the behavior of many-body systems of particles in which the interactions between particles may be strong. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas, and why other properties differ.

A polaron is a quasiparticle used in condensed matter physics to understand the interactions between electrons and atoms in a solid material. The polaron concept was proposed by Lev Landau in 1933 and Solomon Pekar in 1946 to describe an electron moving in a dielectric crystal where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. This lowers the electron mobility and increases the electron's effective mass.

A magnon is a quasiparticle, a collective excitation of the spin structure of an electron in a crystal lattice. In the equivalent wave picture of quantum mechanics, a magnon can be viewed as a quantized spin wave. Magnons carry a fixed amount of energy and lattice momentum, and are spin-1, indicating they obey boson behavior.
Jellium, also known as the uniform electron gas (UEG) or homogeneous electron gas (HEG), is a quantum mechanical model of interacting electrons in a solid where the positive charges are assumed to be uniformly distributed in space; the electron density is a uniform quantity as well in space. This model allows one to focus on the effects in solids that occur due to the quantum nature of electrons and their mutual repulsive interactions without explicit introduction of the atomic lattice and structure making up a real material. Jellium is often used in solid-state physics as a simple model of delocalized electrons in a metal, where it can qualitatively reproduce features of real metals such as screening, plasmons, Wigner crystallization and Friedel oscillations.
A two-dimensional electron gas (2DEG) is a scientific model in solid-state physics. It is an electron gas that is free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels for motion in the third direction, which can then be ignored for most problems. Thus the electrons appear to be a 2D sheet embedded in a 3D world. The analogous construct of holes is called a two-dimensional hole gas (2DHG), and such systems have many useful and interesting properties.
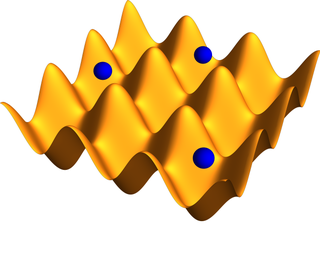
An optical lattice is formed by the interference of counter-propagating laser beams, creating a spatially periodic polarization pattern. The resulting periodic potential may trap neutral atoms via the Stark shift. Atoms are cooled and congregate at the potential extrema. The resulting arrangement of trapped atoms resembles a crystal lattice and can be used for quantum simulation.
The Bose–Hubbard model gives a description of the physics of interacting spinless bosons on a lattice. It is closely related to the Hubbard model that originated in solid-state physics as an approximate description of superconducting systems and the motion of electrons between the atoms of a crystalline solid. The model was introduced by Gersch and Knollman in 1963 in the context of granular superconductors. The model rose to prominence in the 1980s after it was found to capture the essence of the superfluid-insulator transition in a way that was much more mathematically tractable than fermionic metal-insulator models.
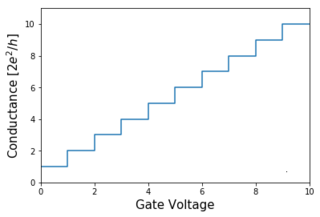
A quantum point contact (QPC) is a narrow constriction between two wide electrically conducting regions, of a width comparable to the electronic wavelength.
A charge density wave (CDW) is an ordered quantum fluid of electrons in a linear chain compound or layered crystal. The electrons within a CDW form a standing wave pattern and sometimes collectively carry an electric current. The electrons in such a CDW, like those in a superconductor, can flow through a linear chain compound en masse, in a highly correlated fashion. Unlike a superconductor, however, the electric CDW current often flows in a jerky fashion, much like water dripping from a faucet due to its electrostatic properties. In a CDW, the combined effects of pinning and electrostatic interactions likely play critical roles in the CDW current's jerky behavior, as discussed in sections 4 & 5 below.
In materials science, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons in unfilled electron bands. Electrons are one type of fermion, and when they are found in such materials, they are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free electron model. The properties of the heavy fermion compounds often derive from the partly filled f-orbitals of rare-earth or actinide ions, which behave like localized magnetic moments.
In applied mathematics, the numerical sign problem is the problem of numerically evaluating the integral of a highly oscillatory function of a large number of variables. Numerical methods fail because of the near-cancellation of the positive and negative contributions to the integral. Each has to be integrated to very high precision in order for their difference to be obtained with useful accuracy.
A Peierls transition or Peierls distortion is a distortion of the periodic lattice of a one-dimensional crystal. Atomic positions oscillate, so that the perfect order of the 1-D crystal is broken.

In condensed matter physics, Luttinger's theorem is a result derived by J. M. Luttinger and J. C. Ward in 1960 that has broad implications in the field of electron transport. It arises frequently in theoretical models of correlated electrons, such as the high-temperature superconductors, and in photoemission, where a metal's Fermi surface can be directly observed.
In condensed matter physics, a quantum spin liquid is a phase of matter that can be formed by interacting quantum spins in certain magnetic materials. Quantum spin liquids (QSL) are generally characterized by their long-range quantum entanglement, fractionalized excitations, and absence of ordinary magnetic order.
In quantum mechanics, orbital magnetization, Morb, refers to the magnetization induced by orbital motion of charged particles, usually electrons in solids. The term "orbital" distinguishes it from the contribution of spin degrees of freedom, Mspin, to the total magnetization. A nonzero orbital magnetization requires broken time-reversal symmetry, which can occur spontaneously in ferromagnetic and ferrimagnetic materials, or can be induced in a non-magnetic material by an applied magnetic field.

In quantum optics, a superradiant phase transition is a phase transition that occurs in a collection of fluorescent emitters, between a state containing few electromagnetic excitations and a superradiant state with many electromagnetic excitations trapped inside the emitters. The superradiant state is made thermodynamically favorable by having strong, coherent interactions between the emitters.
Bose–Einstein condensation can occur in quasiparticles, particles that are effective descriptions of collective excitations in materials. Some have integer spins and can be expected to obey Bose–Einstein statistics like traditional particles. Conditions for condensation of various quasiparticles have been predicted and observed. The topic continues to be an active field of study.

An electron-on-helium qubit is a quantum bit for which the orthonormal basis states |0⟩ and |1⟩ are defined by quantized motional states or alternatively the spin states of an electron trapped above the surface of liquid helium. The electron-on-helium qubit was proposed as the basic element for building quantum computers with electrons on helium by Platzman and Dykman in 1999.


















