't Hooft symbol

Last updated February 21, 2024

The 't Hooft symbol is a collection of numbers which allows one to express the generators of the SU(2) Lie algebra in terms of the generators of Lorentz algebra. The symbol is a blend between the Kronecker delta and the Levi-Civita symbol. It was introduced by Gerard 't Hooft. It is used in the construction of the BPST instanton.

Definition

$\eta _{\mu \nu }^{a}$ is the 't Hooft symbol:

\eta _{\mu \nu }^{a}={\begin{cases}\epsilon ^{a\mu \nu }&\mu ,\nu =1,2,3\\-\delta ^{a\nu }&\mu =4\\\delta ^{a\mu }&\nu =4\\0&\mu =\nu =4\end{cases}}

Where $\delta ^{a\nu }$ and $\delta ^{a\mu }$ are instances of the Kronecker delta, and $\epsilon ^{a\mu \nu }$ is the Levi-Civita symbol.

In other words, they are defined by

( $a=1,2,3;~\mu ,\nu =1,2,3,4;~\epsilon _{1234}=+1$ )

\eta _{a\mu \nu }=\epsilon _{a\mu \nu 4}+\delta _{a\mu }\delta _{\nu 4}-\delta _{a\nu }\delta _{\mu 4}

{\bar {\eta }}_{a\mu \nu }=\epsilon _{a\mu \nu 4}-\delta _{a\mu }\delta _{\nu 4}+\delta _{a\nu }\delta _{\mu 4}

where the latter are the anti-self-dual 't Hooft symbols.

Matrix Form

In matrix form, the 't Hooft symbols are

\eta _{1\mu \nu }={\begin{bmatrix}0&0&0&1\\0&0&1&0\\0&-1&0&0\\-1&0&0&0\end{bmatrix}},\quad \eta _{2\mu \nu }={\begin{bmatrix}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{bmatrix}},\quad \eta _{3\mu \nu }={\begin{bmatrix}0&1&0&0\\-1&0&0&0\\0&0&0&1\\0&0&-1&0\end{bmatrix}},

and their anti-self-duals are the following:

{\bar {\eta }}_{1\mu \nu }={\begin{bmatrix}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{bmatrix}},\quad {\bar {\eta }}_{2\mu \nu }={\begin{bmatrix}0&0&-1&0\\0&0&0&-1\\1&0&0&0\\0&1&0&0\end{bmatrix}},\quad {\bar {\eta }}_{3\mu \nu }={\begin{bmatrix}0&1&0&0\\-1&0&0&0\\0&0&0&-1\\0&0&1&0\end{bmatrix}}.

Properties

They satisfy the self-duality and the anti-self-duality properties:

\eta _{a\mu \nu }={\frac {1}{2}}\epsilon _{\mu \nu \rho \sigma }\eta _{a\rho \sigma }\ ,\qquad {\bar {\eta }}_{a\mu \nu }=-{\frac {1}{2}}\epsilon _{\mu \nu \rho \sigma }{\bar {\eta }}_{a\rho \sigma }\

Some other properties are

\epsilon _{abc}\eta _{b\mu \nu }\eta _{c\rho \sigma }=\delta _{\mu \rho }\eta _{a\nu \sigma }+\delta _{\nu \sigma }\eta _{a\mu \rho }-\delta _{\mu \sigma }\eta _{a\nu \rho }-\delta _{\nu \rho }\eta _{a\mu \sigma }

\eta _{a\mu \nu }\eta _{a\rho \sigma }=\delta _{\mu \rho }\delta _{\nu \sigma }-\delta _{\mu \sigma }\delta _{\nu \rho }+\epsilon _{\mu \nu \rho \sigma }\ ,

\eta _{a\mu \rho }\eta _{b\mu \sigma }=\delta _{ab}\delta _{\rho \sigma }+\epsilon _{abc}\eta _{c\rho \sigma }\ ,

\epsilon _{\mu \nu \rho \theta }\eta _{a\sigma \theta }=\delta _{\sigma \mu }\eta _{a\nu \rho }+\delta _{\sigma \rho }\eta _{a\mu \nu }-\delta _{\sigma \nu }\eta _{a\mu \rho }\ ,

\eta _{a\mu \nu }\eta _{a\mu \nu }=12\ ,\quad \eta _{a\mu \nu }\eta _{b\mu \nu }=4\delta _{ab}\ ,\quad \eta _{a\mu \rho }\eta _{a\mu \sigma }=3\delta _{\rho \sigma }\ .

The same holds for ${\bar {\eta }}$ except for

{\bar {\eta }}_{a\mu \nu }{\bar {\eta }}_{a\rho \sigma }=\delta _{\mu \rho }\delta _{\nu \sigma }-\delta _{\mu \sigma }\delta _{\nu \rho }-\epsilon _{\mu \nu \rho \sigma }\ .

and

\epsilon _{\mu \nu \rho \theta }{\bar {\eta }}_{a\sigma \theta }=-\delta _{\sigma \mu }{\bar {\eta }}_{a\nu \rho }-\delta _{\sigma \rho }{\bar {\eta }}_{a\mu \nu }+\delta _{\sigma \nu }{\bar {\eta }}_{a\mu \rho }\ ,

Obviously $\eta _{a\mu \nu }{\bar {\eta }}_{b\mu \nu }=0$ due to different duality properties.

Many properties of these are tabulated in the appendix of 't Hooft's paper^[1] and also in the article by Belitsky et al.^[2]

Related Research Articles

Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.

In theoretical physics, the Rarita–Schwinger equation is the relativistic field equation of spin-3/2 fermions in a four-dimensional flat spacetime. It is similar to the Dirac equation for spin-1/2 fermions. This equation was first introduced by William Rarita and Julian Schwinger in 1941.

In differential geometry, a tensor density or relative tensor is a generalization of the tensor field concept. A tensor density transforms as a tensor field when passing from one coordinate system to another, except that it is additionally multiplied or weighted by a power W of the Jacobian determinant of the coordinate transition function or its absolute value. A tensor density with a single index is called a vector density. A distinction is made among (authentic) tensor densities, pseudotensor densities, even tensor densities and odd tensor densities. Sometimes tensor densities with a negative weight W are called tensor capacity. A tensor density can also be regarded as a section of the tensor product of a tensor bundle with a density bundle.

In theoretical physics, the superconformal algebra is a graded Lie algebra or superalgebra that combines the conformal algebra and supersymmetry. In two dimensions, the superconformal algebra is infinite-dimensional. In higher dimensions, superconformal algebras are finite-dimensional and generate the superconformal group.

In the theory of general relativity, linearized gravity is the application of perturbation theory to the metric tensor that describes the geometry of spacetime. As a consequence, linearized gravity is an effective method for modeling the effects of gravity when the gravitational field is weak. The usage of linearized gravity is integral to the study of gravitational waves and weak-field gravitational lensing.

In mathematical physics, the gamma matrices, $also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin particles. Gamma matrices were introduced by Paul Dirac in 1928.$

In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the affine connection. It can also be regarded as the gauge field generated by local Lorentz transformations. In some canonical formulations of general relativity, a spin connection is defined on spatial slices and can also be regarded as the gauge field generated by local rotations.

In theoretical physics, a source field is a background field $coupled to the original field as$

In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

In relativistic physics, the electromagnetic stress–energy tensor is the contribution to the stress–energy tensor due to the electromagnetic field. The stress–energy tensor describes the flow of energy and momentum in spacetime. The electromagnetic stress–energy tensor contains the negative of the classical Maxwell stress tensor that governs the electromagnetic interactions.

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.

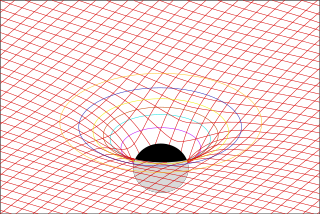
In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.

In theoretical physics, the BPST instanton is the instanton with winding number 1 found by Alexander Belavin, Alexander Polyakov, Albert Schwarz and Yu. S. Tyupkin. It is a classical solution to the equations of motion of SU(2) Yang–Mills theory in Euclidean space-time, meaning it describes a transition between two different topological vacua of the theory. It was originally hoped to open the path to solving the problem of confinement, especially since Polyakov had proven in 1987 that instantons are the cause of confinement in three-dimensional compact-QED. This hope was not realized, however.

The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members often asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— $in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.$

The harmonic coordinate condition is one of several coordinate conditions in general relativity, which make it possible to solve the Einstein field equations. A coordinate system is said to satisfy the harmonic coordinate condition if each of the coordinate functions x^α satisfies d'Alembert's equation. The parallel notion of a harmonic coordinate system in Riemannian geometry is a coordinate system whose coordinate functions satisfy Laplace's equation. Since d'Alembert's equation is the generalization of Laplace's equation to space-time, its solutions are also called "harmonic".

In physics and mathematics, the κ-Poincaré group, named after Henri Poincaré, is a quantum group, obtained by deformation of the Poincaré group into a Hopf algebra. It is generated by the elements $and with the usual constraint:$

The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Since the 8th and 9th centuries, the sine and other trigonometric functions have been used in Islamic mathematics and astronomy, reforming the production of sine tables. Khwarizmi and Habash al-Hasib later produced a set of trigonometric tables.

In mathematical physics, the Belinfante–Rosenfeld tensor is a modification of the stress–energy tensor that is constructed from the canonical stress–energy tensor and the spin current so as to be symmetric yet still conserved.

In mathematical physics, the Dirac equation in curved spacetime is a generalization of the Dirac equation from flat spacetime to curved spacetime, a general Lorentzian manifold.

Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.

References

↑ 't Hooft, G. (1976). "Computation of the quantum effects due to a four-dimensional pseudoparticle". Physical Review D. 14 (12): 3432–3450. Bibcode:1976PhRvD..14.3432T. doi:10.1103/PhysRevD.14.3432.
↑ Belitsky, A. V.; Vandoren, S.; Nieuwenhuizen, P. V. (2000). "Yang-Mills and D-instantons". Classical and Quantum Gravity. 17 (17): 3521–3570. arXiv: hep-th/0004186 . Bibcode:2000CQGra..17.3521B. doi:10.1088/0264-9381/17/17/305. S2CID 16107344.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] 't Hooft, G. (1976). "Computation of the quantum effects due to a four-dimensional pseudoparticle". Physical Review D. 14 (12): 3432–3450. Bibcode:1976PhRvD..14.3432T. doi:10.1103/PhysRevD.14.3432.

[2] Belitsky, A. V.; Vandoren, S.; Nieuwenhuizen, P. V. (2000). "Yang-Mills and D-instantons". Classical and Quantum Gravity. 17 (17): 3521–3570. arXiv: hep-th/0004186 . Bibcode:2000CQGra..17.3521B. doi:10.1088/0264-9381/17/17/305. S2CID 16107344.

[1]

[2]