Related Research Articles

Linear algebra is the branch of mathematics concerning linear equations such as:
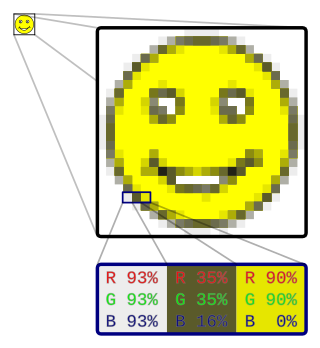
In computer graphics and digital photography, a raster graphic represents a two-dimensional picture as a rectangular matrix or grid of pixels, viewable via a computer display, paper, or other display medium. A raster is technically characterized by the width and height of the image in pixels and by the number of bits per pixel. Raster images are stored in image files with varying dissemination, production, generation, and acquisition formats.

2D computer graphics is the computer-based generation of digital images—mostly from two-dimensional models and by techniques specific to them. It may refer to the branch of computer science that comprises such techniques or to the models themselves.
A blitter is a circuit, sometimes as a coprocessor or a logic block on a microprocessor, dedicated to the rapid movement and modification of data within a computer's memory. A blitter can copy large quantities of data from one memory area to another relatively quickly, and in parallel with the CPU, while freeing up the CPU's more complex capabilities for other operations. A typical use for a blitter is the movement of a bitmap, such as windows and icons in a graphical user interface or images and backgrounds in a 2D video game. The name comes from the bit blit operation of the 1973 Xerox Alto, which stands for bit-block transfer. A blit operation is more than a memory copy, because it can involve data that's not byte aligned, handling transparent pixels, and various ways of combining the source and destination data.
Computer science is the study of the theoretical foundations of information and computation and their implementation and application in computer systems. One well known subject classification system for computer science is the ACM Computing Classification System devised by the Association for Computing Machinery.
In parallel computer architectures, a systolic array is a homogeneous network of tightly coupled data processing units (DPUs) called cells or nodes. Each node or DPU independently computes a partial result as a function of the data received from its upstream neighbours, stores the result within itself and passes it downstream. Systolic arrays were first used in Colossus, which was an early computer used to break German Lorenz ciphers during World War II. Due to the classified nature of Colossus, they were independently invented or rediscovered by H. T. Kung and Charles Leiserson who described arrays for many dense linear algebra computations for banded matrices. Early applications include computing greatest common divisors of integers and polynomials. They are sometimes classified as multiple-instruction single-data (MISD) architectures under Flynn's taxonomy, but this classification is questionable because a strong argument can be made to distinguish systolic arrays from any of Flynn's four categories: SISD, SIMD, MISD, MIMD, as discussed later in this article.

Ray casting is the methodological basis for 3D CAD/CAM solid modeling and image rendering. It is essentially the same as ray tracing for computer graphics where virtual light rays are "cast" or "traced" on their path from the focal point of a camera through each pixel in the camera sensor to determine what is visible along the ray in the 3D scene. The term "Ray Casting" was introduced by Scott Roth while at the General Motors Research Labs from 1978–1980. His paper, "Ray Casting for Modeling Solids", describes modeled solid objects by combining primitive solids, such as blocks and cylinders, using the set operators union (+), intersection (&), and difference (-). The general idea of using these binary operators for solid modeling is largely due to Voelcker and Requicha's geometric modelling group at the University of Rochester. See solid modeling for a broad overview of solid modeling methods. This figure on the right shows a U-Joint modeled from cylinders and blocks in a binary tree using Roth's ray casting system in 1979.

A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information".
Basic Linear Algebra Subprograms (BLAS) is a specification that prescribes a set of low-level routines for performing common linear algebra operations such as vector addition, scalar multiplication, dot products, linear combinations, and matrix multiplication. They are the de facto standard low-level routines for linear algebra libraries; the routines have bindings for both C and Fortran. Although the BLAS specification is general, BLAS implementations are often optimized for speed on a particular machine, so using them can bring substantial performance benefits. BLAS implementations will take advantage of special floating point hardware such as vector registers or SIMD instructions.

In computer graphics, a shader is a computer program that calculates the appropriate levels of light, darkness, and color during the rendering of a 3D scene—a process known as shading. Shaders have evolved to perform a variety of specialized functions in computer graphics special effects and video post-processing, as well as general-purpose computing on graphics processing units.
General-purpose computing on graphics processing units is the use of a graphics processing unit (GPU), which typically handles computation only for computer graphics, to perform computation in applications traditionally handled by the central processing unit (CPU). The use of multiple video cards in one computer, or large numbers of graphics chips, further parallelizes the already parallel nature of graphics processing.

Pixel art scaling algorithms are graphical filters that attempt to enhance the appearance of hand-drawn 2D pixel art graphics. These algorithms are a form of automatic image enhancement. Pixel art scaling algorithms employ methods significantly different than the common methods of image rescaling, which have the goal of preserving the appearance of images.
Clipping, in the context of computer graphics, is a method to selectively enable or disable rendering operations within a defined region of interest. Mathematically, clipping can be described using the terminology of constructive geometry. A rendering algorithm only draws pixels in the intersection between the clip region and the scene model. Lines and surfaces outside the view volume are removed.

Ordered dithering is any image dithering algorithm which uses a pre-set threshold map tiled across an image. It is commonly used to display a continuous image on a display of smaller color depth. For example, Microsoft Windows uses it in 16-color graphics modes. The algorithm is characterized by noticeable crosshatch patterns in the result.
A multidimensional signal is a function of M independent variables where . Real world signals, which are generally continuous time signals, have to be discretized (sampled) in order to ensure that digital systems can be used to process the signals. It is during this process of discretization where sampling comes into picture. Although there are many ways of obtaining a discrete representation of a continuous time signal, periodic sampling is by far the simplest scheme. Theoretically, sampling can be performed with respect to any set of points. But practically, sampling is carried out with respect to a set of points that have a certain algebraic structure. Such structures are called lattices. Mathematically, the process of sampling an -dimensional signal can be written as:
In computing, a compute kernel is a routine compiled for high throughput accelerators, separate from but used by a main program. They are sometimes called compute shaders, sharing execution units with vertex shaders and pixel shaders on GPUs, but are not limited to execution on one class of device, or graphics APIs.
This is a glossary of terms relating to computer graphics.
Kernel-phases are observable quantities used in high resolution astronomical imaging used for superresolution image creation. It can be seen as a generalization of closure phases for redundant arrays. For this reason, when the wavefront quality requirement are met, it is an alternative to aperture masking interferometry that can be executed without a mask while retaining phase error rejection properties. The observables are computed through linear algebra from the Fourier transform of direct images. They can then be used for statistical testing, model fitting, or image reconstruction.
References
- ↑ R. Brunelli and C. M. Modena, "ANIMAL: AN IMage ALgebra", High Frequency, 1989, LVIII:3:255-259