Related Research Articles

Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconducting phase exhibited by certain materials at extremely low cryogenic temperature, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, and the Bose–Einstein condensate found in ultracold atomic systems. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other physics theories to develop mathematical models.
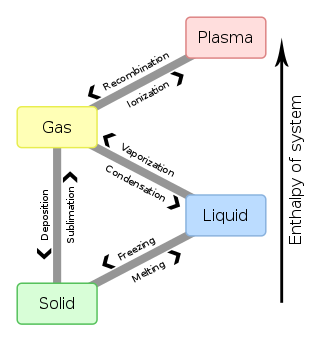
In chemistry, thermodynamics, and other related fields, a phase transition is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point.

Samuel Chao Chung Ting is an American physicist who, with Burton Richter, received the Nobel Prize in 1976 for discovering the subatomic J/ψ particle. More recently he has been the principal investigator in research conducted with the Alpha Magnetic Spectrometer, a device installed on the International Space Station in 2011.

In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change i.e. a minimum in electrical resistivity with temperature. The cause of the effect was first explained by Jun Kondo, who applied third-order perturbation theory to the problem to account for scattering of s-orbital conduction electrons off d-orbital electrons localized at impurities. Kondo's calculation predicted that the scattering rate and the resulting part of the resistivity should increase logarithmically as the temperature approaches 0 K. Experiments in the 1960s by Myriam Sarachik at Bell Laboratories provided the first data that confirmed the Kondo effect. Extended to a lattice of magnetic impurities, the Kondo effect likely explains the formation of heavy fermions and Kondo insulators in intermetallic compounds, especially those involving rare earth elements such as cerium, praseodymium, and ytterbium, and actinide elements such as uranium. The Kondo effect has also been observed in quantum dot systems.
In condensed matter physics, the term geometrical frustration refers to a phenomenon where atoms tend to stick to non-trivial positions or where, on a regular crystal lattice, conflicting inter-atomic forces lead to quite complex structures. As a consequence of the frustration in the geometry or in the forces, a plenitude of distinct ground states may result at zero temperature, and usual thermal ordering may be suppressed at higher temperatures. Much studied examples are amorphous materials, glasses, or dilute magnets.
Critical exponents describe the behavior of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e. they do not depend on the details of the physical system, but only on some of its general features. For instance, for ferromagnetic systems, the critical exponents depend only on:
Per Bak was a Danish theoretical physicist who coauthored the 1987 academic paper that coined the term "self-organized criticality."
A charge density wave (CDW) is an ordered quantum fluid of electrons in a linear chain compound or layered crystal. The electrons within a CDW form a standing wave pattern and sometimes collectively carry an electric current. The electrons in such a CDW, like those in a superconductor, can flow through a linear chain compound en masse, in a highly correlated fashion. Unlike a superconductor, however, the electric CDW current often flows in a jerky fashion, much like water dripping from a faucet due to its electrostatic properties. In a CDW, the combined effects of pinning and electrostatic interactions likely play critical roles in the CDW current's jerky behavior, as discussed in sections 4 & 5 below.

The Landau–Zener formula is an analytic solution to the equations of motion governing the transition dynamics of a two-state quantum system, with a time-dependent Hamiltonian varying such that the energy separation of the two states is a linear function of time. The formula, giving the probability of a diabatic transition between the two energy states, was published separately by Lev Landau, Clarence Zener, Ernst Stueckelberg, and Ettore Majorana, in 1932.
Walter Selke is a German retired professor for Theoretical Physics at the RWTH Aachen.
The Wolff algorithm, named after Ulli Wolff, is an algorithm for Monte Carlo simulation of the Ising model and Potts model in which the unit to be flipped is not a single spin but a cluster of them. This cluster is defined as the set of connected spins sharing the same spin states, based on the Fortuin-Kasteleyn representation.
A spin model is a mathematical model used in physics primarily to explain magnetism. Spin models may either be classical or quantum mechanical in nature. Spin models have been studied in quantum field theory as examples of integrable models. Spin models are also used in quantum information theory and computability theory in theoretical computer science. The theory of spin models is a far reaching and unifying topic that cuts across many fields.

Subir Sachdev is Herchel Smith Professor of Physics at Harvard University specializing in condensed matter. He was elected to the U.S. National Academy of Sciences in 2014, and received the Lars Onsager Prize from the American Physical Society and the Dirac Medal from the ICTP in 2018. He was a co-editor of the Annual Review of Condensed Matter Physics from 2017–2019.
A composite fermion is the topological bound state of an electron and an even number of quantized vortices, sometimes visually pictured as the bound state of an electron and, attached, an even number of magnetic flux quanta. Composite fermions were originally envisioned in the context of the fractional quantum Hall effect, but subsequently took on a life of their own, exhibiting many other consequences and phenomena.

Piers Coleman is a British-born theoretical physicist, working in the field of theoretical condensed matter physics. Coleman is professor of physics at Rutgers University in New Jersey and at Royal Holloway, University of London.
The Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) phase can arise in a superconductor in large magnetic field. Among its characteristics are Cooper pairs with nonzero total momentum and a spatially non-uniform order parameter, leading to normal conducting areas in the superconductor.
In condensed matter physics, a quantum spin liquid is a phase of matter that can be formed by interacting quantum spins in certain magnetic materials. Quantum spin liquids (QSL) are generally characterized by their long-range quantum entanglement, fractionalized excitations, and absence of ordinary magnetic order.
Arthur Brooks Harris, called Brooks Harris, is an American physicist.
Shang-keng Ma was a Chinese theoretical physicist, known for his work on the theory of critical phenomena and random systems. He is known as the co-author with Bertrand Halperin and Pierre Hohenberg of a 1972 paper that "generalized the renormalization group theory to dynamical critical phenomena." Ma is also known as the co-author with Yoseph Imry of a 1975 paper and with Amnon Aharony and Imry of a 1976 paper that established the foundation of the random field Ising model (RFIM)
David Alan Huse is an American theoretical physicist, specializing in statistical physics and condensed matter physics.
References
- ↑ R. J. Elliott (1961). "Phenomenological discussion of magnetic ordering in the heavy rare-earth metals". Phys. Rev. 124 (2): 346–353. Bibcode:1961PhRv..124..346E. doi:10.1103/PhysRev.124.346.
- ↑ M.E. Fisher and W. Selke (1980). "Infinitely many commensurate phases in a simple Ising model". Phys. Rev. Lett. 44 (23): 1502–1505. Bibcode:1980PhRvL..44.1502F. doi:10.1103/PhysRevLett.44.1502.
- ↑ P. Bak (1982). "Commensurate phases, incommensurate phases, and the devil's staircase". Reports on Progress in Physics. 45 (6): 587–629. Bibcode:1982RPPh...45..587B. CiteSeerX 10.1.1.131.4735 . doi:10.1088/0034-4885/45/6/001.
- ↑ W. Selke (1988). "The ANNNI model—Theoretical analysis and experimental application". Physics Reports. 170 (4): 213–264. Bibcode:1988PhR...170..213S. doi:10.1016/0370-1573(88)90140-8.