Commensurability (mathematics)

Last updated July 22, 2023

In mathematics, two non-zero real numbers a and b are said to be commensurable if their ratio a/b is a rational number; otherwise a and b are called incommensurable. (Recall that a rational number is one that is equivalent to the ratio of two integers.) There is a more general notion of commensurability in group theory.

For example, the numbers 3 and 2 are commensurable because their ratio, 3/2, is a rational number. The numbers ${\sqrt {3}}$ and $2{\sqrt {3}}$ are also commensurable because their ratio, ${\textstyle {\frac {\sqrt {3}}{2{\sqrt {3}}}}={\frac {1}{2}}}$ , is a rational number. However, the numbers ${\textstyle {\sqrt {3}}}$ and 2 are incommensurable because their ratio, ${\textstyle {\frac {\sqrt {3}}{2}}}$ , is an irrational number.

More generally, it is immediate from the definition that if a and b are any two non-zero rational numbers, then a and b are commensurable; it is also immediate that if a is any irrational number and b is any non-zero rational number, then a and b are incommensurable. On the other hand, if both a and b are irrational numbers, then a and b may or may not be commensurable.

History of the concept

The Pythagoreans are credited with the proof of the existence of irrational numbers.^[1]^[2] When the ratio of the lengths of two line segments is irrational, the line segments themselves (not just their lengths) are also described as being incommensurable.

A separate, more general and circuitous ancient Greek doctrine of proportionality for geometric magnitude was developed in Book V of Euclid's Elements in order to allow proofs involving incommensurable lengths, thus avoiding arguments which applied only to a historically restricted definition of number.

Euclid's notion of commensurability is anticipated in passing in the discussion between Socrates and the slave boy in Plato's dialogue entitled Meno, in which Socrates uses the boy's own inherent capabilities to solve a complex geometric problem through the Socratic Method. He develops a proof which is, for all intents and purposes, very Euclidean in nature and speaks to the concept of incommensurability.^[3]

The usage primarily comes from translations of Euclid's Elements, in which two line segments a and b are called commensurable precisely if there is some third segment c that can be laid end-to-end a whole number of times to produce a segment congruent to a, and also, with a different whole number, a segment congruent to b. Euclid did not use any concept of real number, but he used a notion of congruence of line segments, and of one such segment being longer or shorter than another.

That a/b is rational is a necessary and sufficient condition for the existence of some real number c, and integers m and n, such that

a = mc and b = nc.

Assuming for simplicity that a and b are positive, one can say that a ruler, marked off in units of length c, could be used to measure out both a line segment of length a, and one of length b. That is, there is a common unit of length in terms of which a and b can both be measured; this is the origin of the term. Otherwise the pair a and b are incommensurable.

In group theory

In group theory, two subgroups Γ₁ and Γ₂ of a group G are said to be commensurable if the intersection Γ₁ ∩ Γ₂ is of finite index in both Γ₁ and Γ₂.

Example: Let a and b be nonzero real numbers. Then the subgroup of the real numbers R generated by a is commensurable with the subgroup generated by b if and only if the real numbers a and b are commensurable, in the sense that a/b is rational. Thus the group-theoretic notion of commensurability generalizes the concept for real numbers.

There is a similar notion for two groups which are not given as subgroups of the same group. Two groups G₁ and G₂ are (abstractly) commensurable if there are subgroups H₁ ⊂ G₁ and H₂ ⊂ G₂ of finite index such that H₁ is isomorphic to H₂.

In topology

Two path-connected topological spaces are sometimes said to be commensurable if they have homeomorphic finite-sheeted covering spaces. Depending on the type of space under consideration, one might want to use homotopy equivalences or diffeomorphisms instead of homeomorphisms in the definition. If two spaces are commensurable, then their fundamental groups are commensurable.

Example: any two closed surfaces of genus at least 2 are commensurable with each other.

Related Research Articles

An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer coefficients. For example, the golden ratio, $, is an algebraic number, because it is a root of the polynomial x 2 - x - 1 . That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number is algebraic because it is a root of x 4 + 4 .$

In mathematics, a Cauchy sequence, named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses. More precisely, given any small positive distance, all but a finite number of elements of the sequence are less than that given distance from each other.

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities $and with,$

In mathematics, a square root of a number $x$ is a number $y$ such that $; in other words, a number y whose square is x . For example, 4 and -4 are square roots of 16 because .$

<span class="mw-page-title-main">Similarity (geometry)</span> Same shape, up to a scaling

In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

In mathematics, Dedekind cuts, named after German mathematician Richard Dedekind but previously considered by Joseph Bertrand, are а method of construction of the real numbers from the rational numbers. A Dedekind cut is a partition of the rational numbers into two sets A and B, such that all elements of A are less than all elements of B, and A contains no greatest element. The set B may or may not have a smallest element among the rationals. If B has a smallest element among the rationals, the cut corresponds to that rational. Otherwise, that cut defines a unique irrational number which, loosely speaking, fills the "gap" between A and B. In other words, A contains every rational number less than the cut, and B contains every rational number greater than or equal to the cut. An irrational cut is equated to an irrational number which is in neither set. Every real number, rational or not, is equated to one and only one cut of rationals.

<span class="mw-page-title-main">Ratio</span> Relationship between two numbers of the same kind

In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six. Similarly, the ratio of lemons to oranges is 6:8 and the ratio of oranges to the total amount of fruit is 8:14.

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x⁻¹, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the function f(x) that maps x to 1/x, is one of the simplest examples of a function which is its own inverse (an involution).

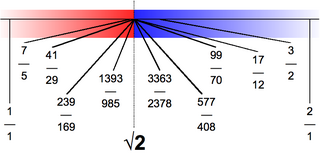
In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria.

In mathematics, a quadratic irrational number is an irrational number that is the solution to some quadratic equation with rational coefficients which is irreducible over the rational numbers. Since fractions in the coefficients of a quadratic equation can be cleared by multiplying both sides by their least common denominator, a quadratic irrational is an irrational root of some quadratic equation with integer coefficients. The quadratic irrational numbers, a subset of the complex numbers, are algebraic numbers of degree 2, and can therefore be expressed as

In mathematics, the modular group is the projective special linear group $of 2 × 2 matrices with integer coefficients and determinant 1. The matrices A and −A are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic.$

The square root of 2 is a positive real number that, when multiplied by itself, equals the number 2. It may be written in mathematics as $or, and is an algebraic number. Technically, it should be called the principal square root of 2, to distinguish it from the negative number with the same property.$

In mathematics, a proof by infinite descent, also known as Fermat's method of descent, is a particular kind of proof by contradiction used to show that a statement cannot possibly hold for any number, by showing that if the statement were to hold for a number, then the same would be true for a smaller number, leading to an infinite descent and ultimately a contradiction. It is a method which relies on the well-ordering principle, and is often used to show that a given equation, such as a Diophantine equation, has no solutions.

In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object by creating or providing a method for creating the object. This is in contrast to a non-constructive proof, which proves the existence of a particular kind of object without providing an example. For avoiding confusion with the stronger concept that follows, such a constructive proof is sometimes called an effective proof.

In mathematics, a Fuchsian group is a discrete subgroup of PSL(2,R). The group PSL(2,R) can be regarded equivalently as a group of orientation-preserving isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting on any of these spaces. There are some variations of the definition: sometimes the Fuchsian group is assumed to be finitely generated, sometimes it is allowed to be a subgroup of PGL(2,R), and sometimes it is allowed to be a Kleinian group which is conjugate to a subgroup of PSL(2,R).

In mathematics an even integer, that is, a number that is divisible by 2, is called evenly even or doubly even if it is a multiple of 4, and oddly even or singly even if it is not. The former names are traditional ones, derived from ancient Greek mathematics; the latter have become common in recent decades.

<span class="mw-page-title-main">Rational number</span> Quotient of two integers

In mathematics, a rational number is a number that can be expressed as the quotient or fraction $of two integers, a numerator p and a non-zero denominator q . For example, is a rational number, as is every integer. The set of all rational numbers, also referred to as " the rationals ", the field of rationals or the field of rational numbers is usually denoted by boldface Q, or blackboard bold$

In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being incommensurable, meaning that they share no "measure" in common, that is, there is no length, no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself.

In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.

In mathematics, specifically in group theory, two groups are commensurable if they differ only by a finite amount, in a precise sense. The commensurator of a subgroup is another subgroup, related to the normalizer.

References

↑ Kurt von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021.
↑ James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal. 11 (5): 312–316. doi:10.2307/3026893. JSTOR 3026893.
↑ Plato's Meno. Translated with annotations by George Anastaplo and Laurence Berns. Focus Publishing: Newburyport, MA. 2004. ISBN 0-941051-71-4

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Kurt von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021.

[2] James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal. 11 (5): 312–316. doi:10.2307/3026893. JSTOR 3026893.

[3] Plato's Meno. Translated with annotations by George Anastaplo and Laurence Berns. Focus Publishing: Newburyport, MA. 2004. ISBN 0-941051-71-4

[1]

[2]

[3]