
Euclidean geometry is a mathematical system attributed to Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.

In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.

In Euclidean geometry, two objects are similar if they both have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those specifying Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises when either the metric requirement is relaxed, or the parallel postulate is replaced with an alternative one. In the latter case one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras which give rise to kinematic geometries that have also been called non-Euclidean geometry.

In elementary geometry, the property of being perpendicular (perpendicularity) is the relationship between two lines which meet at a right angle. The property extends to other related geometric objects.

Synthetic geometry is the study of geometry without the use of coordinates or formulae. It relies on the axiomatic method and the tools directly related to them, that is, compass and straightedge, to draw conclusions and solve problems.

Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates, but since these are not sufficient as a basis of Euclidean geometry, other systems, such as Hilbert's axioms without the parallel axiom, are used. The term was introduced by János Bolyai in 1832. It is sometimes referred to as neutral geometry, as it is neutral with respect to the parallel postulate.
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie as the foundation for a modern treatment of Euclidean geometry. Other well-known modern axiomatizations of Euclidean geometry are those of Alfred Tarski and of George Birkhoff.
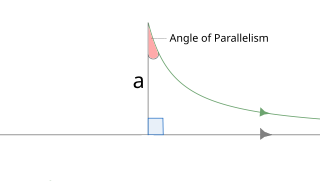
In hyperbolic geometry, the angle of parallelism , is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
Tarski's axioms, due to Alfred Tarski, are an axiom set for the substantial fragment of Euclidean geometry that is formulable in first-order logic with identity, and requiring no set theory. Other modern axiomizations of Euclidean geometry are Hilbert's axioms and Birkhoff's axioms.

In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
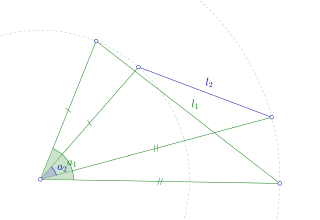
In geometry, the hinge theorem states that if two sides of one triangle are congruent to two sides of another triangle, and the included angle of the first is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second triangle. This theorem is actually Propositions 24 of Book 1 of Euclid's Elements. The theorem states the following:
If two sides of one triangle are congruent, respectively, to two sides of a second triangle, and the included angle of the first triangle is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second.

A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book Euclides ab omni naevo vindicatus first published in 1733, an attempt to prove the parallel postulate using the method Reductio ad absurdum.
In geometry, Pasch's axiom is a statement in plane geometry, used implicitly by Euclid, which cannot be derived from the postulates as Euclid gave them. Its essential role was discovered by Moritz Pasch in 1882.

In geometry, a transversal is a line that passes through two lines in the same plane at two distinct points. Transversals play a role in establishing whether two other lines in the Euclidean plane are parallel. The intersections of a transversal with two lines create various types of pairs of angles: consecutive interior angles, corresponding angles, and alternate angles. As a consequence of Euclid's parallel postulate, if the two lines are parallel, consecutive interior angles are supplementary, corresponding angles are equal, and alternate angles are equal.
Ordered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement. Ordered geometry is a fundamental geometry forming a common framework for affine, Euclidean, absolute, and hyperbolic geometry.
The exterior angle theorem is Proposition 1.16 in Euclid's Elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. This is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

In mathematics, the Pythagorean theorem, also known as Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the "Pythagorean equation":












