Nicomedes (mathematician)

Last updated
Conchoids of line with common center. Conchoid of Nicomedes.png
Conchoids of line with common center.
Conchoid of Nicomedes drawn by an apparatus illustrated in Eutocius' Commentaries on the works of Archimedes Nicomedes.gif
Conchoid of Nicomedes drawn by an apparatus illustrated in Eutocius' Commentaries on the works of Archimedes

Nicomedes ( /ˌnɪkəˈmiːdiːz/ ; Greek : Νικομήδης; c. 280 – c. 210 BC) was an ancient Greek mathematician.

Greek language language spoken in Greece, Cyprus and Southern Albania

Greek is an independent branch of the Indo-European family of languages, native to Greece, Cyprus and other parts of the Eastern Mediterranean and the Black Sea. It has the longest documented history of any living Indo-European language, spanning more than 3000 years of written records. Its writing system has been the Greek alphabet for the major part of its history; other systems, such as Linear B and the Cypriot syllabary, were used previously. The alphabet arose from the Phoenician script and was in turn the basis of the Latin, Cyrillic, Armenian, Coptic, Gothic, and many other writing systems.

Ancient Greek Version of the Greek language used from roughly the 9th century BCE to the 6th century CE

The Ancient Greek language includes the forms of Greek used in Ancient Greece and the ancient world from around the 9th century BCE to the 6th century CE. It is often roughly divided into the Archaic period, Classical period, and Hellenistic period. It is antedated in the second millennium BCE by Mycenaean Greek and succeeded by medieval Greek.

Mathematician person with an extensive knowledge of mathematics

A mathematician is someone who uses an extensive knowledge of mathematics in his or her work, typically to solve mathematical problems.

Contents

Life and work

Almost nothing is known about Nicomedes' life apart from references in his works. Studies have stated that Nicomedes was born in about 280 BC and died in about 210 BC. It is known that he lived around the time of Eratosthenes or after, because he criticized Eratosthenes' method of doubling the cube. It is also known that Apollonius of Perga called a curve of his creation a "sister of the conchoid", suggesting that he was naming it after Nicomedes' already famous curve. Consequently, it is believed that Nicomedes lived after Eratosthenes and before Apollonius of Perga.

Eratosthenes ancient Greek scientist

Eratosthenes of Cyrene was a Greek mathematician, geographer, poet, astronomer, and music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria. He invented the discipline of geography, including the terminology used today.

Doubling the cube geometric problem of constructing a cube with twice the volume of a given cube, not possible with compass and straightedge

Doubling the cube, also known as the Delian problem, is an ancient geometric problem. Given the edge of a cube, the problem requires the construction of the edge of a second cube whose volume is double that of the first. As with the related problems of squaring the circle and trisecting the angle, doubling the cube is now known to be impossible using only a compass and straightedge, but even in ancient times solutions were known that employed other tools.

Apollonius of Perga Ancient Greek geometer and astronomer noted for his writings on conic sections

Apollonius of Perga was a Greek geometer and astronomer known for his theories on the topic of conic sections. Beginning from the theories of Euclid and Archimedes on the topic, he brought them to the state they were in just before the invention of analytic geometry. His definitions of the terms ellipse, parabola, and hyperbola are the ones in use today.

Like many geometers of the time, Nicomedes was engaged in trying to solve the problems of doubling the cube and trisecting the angle, both problems we now understand to be impossible using the tools of classical geometry. In the course of his investigations, Nicomedes created the conchoid [1] of Nicomedes; a discovery that is contained in his famous work entitled On conchoid lines. Nicomedes discovered three distinct types of conchoids, now unknown. Pappus wrote: "Nicomedes trisected any rectilinear angle by means of the conchoidal curves, the construction, order and properties of which he handed down, being himself the discoverer of their peculiar character". [2]

Geometry branch of mathematics that measures the shape, size and position of objects

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

Conchoid (mathematics)

A conchoid is a curve derived from a fixed point O, another curve, and a length d. It was invented by the ancient Greek mathematician Nicomedes.

Pappus of Alexandria Greek mathematician of Antiquity

Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge (Συναγωγή) or Collection, and for Pappus's hexagon theorem in projective geometry. Nothing is known of his life, other than, that he had a son named Hermodorus, and was a teacher in Alexandria.

Nicomedes also used the Hippias' quadratrix to square the circle, since according to Pappus, "For the squaring of the circle there was used by Dinostratus, Nicomedes, and certain other later persons a certain curve which took its name from this property, for it is called by them square-forming". [2] Eutocius mentions that Nicomedes "prided himself inordinately on his discovery of this curve, contrasting it with Eratosthenes's mechanism for finding any number of mean proportionals, to which he objected formally and at length on the ground that it was impracticable and entirely outside the spirit of geometry". [2]

Hippias of Elis was a Greek sophist, and a contemporary of Socrates. With an assurance characteristic of the later sophists, he claimed to be regarded as an authority on all subjects, and lectured on poetry, grammar, history, politics, mathematics, and much else. Most of our knowledge of him is derived from Plato, who characterizes him as vain and arrogant.

In mathematics, a quadratrix is a curve having ordinates which are a measure of the area of another curve. The two most famous curves of this class are those of Dinostratus and E. W. Tschirnhaus, which are both related to the circle.

Squaring the circle geometric problem

Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge. It may be taken to ask whether specified axioms of Euclidean geometry concerning the existence of lines and circles entail the existence of such a square.

Citations and footnotes

  1. ↑ Wikisource-logo.svg Chisholm, Hugh, ed. (1911). "Conchoid". Encyclopædia Britannica . 6 (11th ed.). Cambridge University Press. pp. 826–827.
  2. 1 2 3 Heath (1921)

Related Research Articles

Euclid Greek mathematician, inventor of axiomatic geometry

Euclid, sometimes called Euclid of Alexandria to distinguish him from Euclid of Megara, was a Greek mathematician, often referred to as the "founder of geometry" or the "father of geometry". He was active in Alexandria during the reign of Ptolemy I. His Elements is one of the most influential works in the history of mathematics, serving as the main textbook for teaching mathematics from the time of its publication until the late 19th or early 20th century. In the Elements, Euclid deduced the theorems of what is now called Euclidean geometry from a small set of axioms. Euclid also wrote works on perspective, conic sections, spherical geometry, number theory, and mathematical rigour.

History of geometry Wikimedia history article

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).

History of mathematics aspect of history

The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. From 3000 BC the Mesopotamian states of Sumer, Akkad and Assyria, together with Ancient Egypt and Ebla began using arithmetic, algebra and geometry for purposes of taxation, commerce, trade and also in the field of astronomy and to formulate calendars and record time.

Straightedge and compass construction way of drawing geometric objects

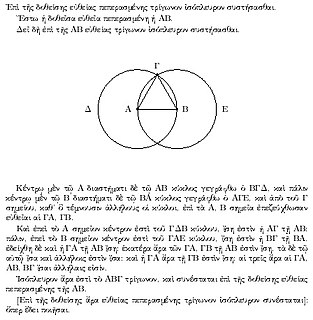
Straightedge and compass construction, also known as ruler-and-compass construction or classical construction, is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass.

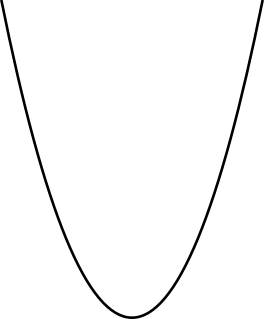
Curve object similar to a line but which is not required to be straight

In mathematics, a curve is, generally speaking, an object similar to a line but that need not be straight. Thus, a curve is a generalization of a line, in that its curvature need not be zero.

Angle trisection the construction of an angle equal to one third a given angle

Angle trisection is a classical problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.

Dandelin spheres

In geometry, the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and the plane is a conic section, and the point at which either sphere touches the plane is a focus of the conic section, so the Dandelin spheres are also sometimes called focal spheres.

Diocles was a Greek mathematician and geometer.

Menaechmus was an ancient Greek mathematician and geometer born in Alopeconnesus in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube using the parabola and hyperbola.

Dinostratus was a Greek mathematician and geometer, and the brother of Menaechmus. He is known for using the quadratrix to solve the problem of squaring the circle.

Neusis construction

The neusis is a geometric construction method that was used in antiquity by Greek mathematicians.

Hypsicles was an ancient Greek mathematician and astronomer known for authoring On Ascensions (Ἀναφορικός) and the Book XIV of Euclid's Elements. Hypsicles lived in Alexandria.

Serenus of Antinoupolis was a Greek mathematician of the Roman Imperial Period.

Carpus of Antioch was an ancient Greek mathematician. It is not certain when he lived; he may have lived any time between the 2nd century BC and the 2nd century AD. He wrote on mechanics, astronomy, and geometry. Proclus quotes from an Astronomical Treatise by Carpus concerning whether problems should come before theorems, in which Carpus may have been criticising Geminus. Proclus also quotes the view of Carpus that "an angle is a quantity, namely a distance between the lines of surfaces containing it." According to Pappus, Carpus made use of mathematics for practical applications. According to Iamblichus, Carpus also constructed a curve for the purpose of squaring the circle, which he calls a curve generated by a double motion.

On Spirals is a treatise by Archimedes, written around 225 BC. Although Archimedes did not discover the Archimedean spiral, he employed it in this book to square the circle and trisect an angle.

A timeline of algebra and geometry

Quadratrix of Hippias

The quadratrix or trisectrix of Hippias is a curve, which is created by a uniform motion. It is one of the oldest examples for a kinematic curve, that is a curve created through motion. Its discovery is attributed to the Greek sophist Hippias of Elis, who used it around 420 BC in an attempt to solve the angle trisection problem. Later around 350 BC Dinostratus used it in an attempt to solve the problem of squaring the circle.

References

Edmund Frederick Robertson is a Professor emeritus of pure mathematics at the University of St Andrews.

The MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland. It contains detailed biographies on many historical and contemporary mathematicians, as well as information on famous curves and various topics in the history of mathematics.

University of St Andrews university in St Andrews, Fife, Scotland

The University of St Andrews is a British public university in St Andrews, Fife, Scotland. It is the oldest of the four ancient universities of Scotland and the third oldest university in the English-speaking world. St Andrews was founded between 1410 and 1413, when the Avignon Antipope Benedict XIII issued a papal bull to a small founding group of Augustinian clergy.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.