Exterior angle theorem

Last updated

The exterior angle theorem is Proposition 1.16 in Euclid's Elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. This is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate.

Contents

In several high school treatments of geometry, the term "exterior angle theorem" has been applied to a different result, [1] namely the portion of Proposition 1.32 which states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. This result, which depends upon Euclid's parallel postulate will be referred to as the "High school exterior angle theorem" (HSEAT) to distinguish it from Euclid's exterior angle theorem.

Some authors refer to the "High school exterior angle theorem" as the strong form of the exterior angle theorem and "Euclid's exterior angle theorem" as the weak form. [2]

Exterior angles

A triangle has three corners, called vertices. The sides of a triangle (line segments) that come together at a vertex form two angles (four angles if you consider the sides of the triangle to be lines instead of line segments). [3] Only one of these angles contains the third side of the triangle in its interior, and this angle is called an interior angle of the triangle. [4] In the picture below, the angles ∠ABC, ∠BCA and ∠CAB are the three interior angles of the triangle. An exterior angle is formed by extending one of the sides of the triangle; the angle between the extended side and the other side is the exterior angle. In the picture, angle ∠ACD is an exterior angle.

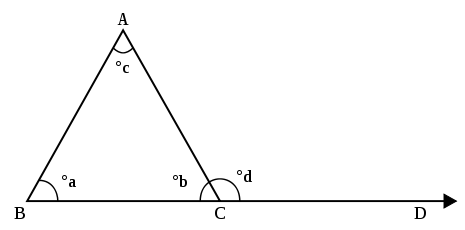Remint3.svg

Euclid's exterior angle theorem

The proof of Proposition 1.16 given by Euclid is often cited as one place where Euclid gives a flawed proof. [5] [6] [7]

Euclid proves the exterior angle theorem by:

By congruent triangles we can conclude that ∠ BAC = ∠ ECF and ∠ ECF is smaller than ∠ ECD, ∠ ECD = ∠ ACD therefore ∠ BAC is smaller than ∠ ACD and the same can be done for the angle ∠ CBA by bisecting BC.

The flaw lies in the assumption that a point (F, above) lies "inside" angle (∠ ACD). No reason is given for this assertion, but the accompanying diagram makes it look like a true statement. When a complete set of axioms for Euclidean geometry is used (see Foundations of geometry) this assertion of Euclid can be proved. [8]

Invalidity in spherical geometry

Small triangles may behave in a nearly Euclidean manner, but the exterior angles at the base of the large triangle are 90deg, a contradiction to the Euclid's exterior angle theorem. Triangles (spherical geometry).jpg
Small triangles may behave in a nearly Euclidean manner, but the exterior angles at the base of the large triangle are 90°, a contradiction to the Euclid's exterior angle theorem.

The exterior angle theorem is not valid in spherical geometry nor in the related elliptical geometry. Consider a spherical triangle one of whose vertices is the North Pole and the other two lie on the equator. The sides of the triangle emanating from the North Pole (great circles of the sphere) both meet the equator at right angles, so this triangle has an exterior angle that is equal to a remote interior angle. The other interior angle (at the North Pole) can be made larger than 90°, further emphasizing the failure of this statement. However, since the Euclid's exterior angle theorem is a theorem in absolute geometry it is automatically valid in hyperbolic geometry.

High school exterior angle theorem

The high school exterior angle theorem (HSEAT) says that the size of an exterior angle at a vertex of a triangle equals the sum of the sizes of the interior angles at the other two vertices of the triangle (remote interior angles). So, in the picture, the size of angle ACD equals the size of angle ABC plus the size of angle CAB.

The HSEAT is logically equivalent to the Euclidean statement that the sum of angles of a triangle is 180°. If it is known that the sum of the measures of the angles in a triangle is 180°, then the HSEAT is proved as follows:

On the other hand, if the HSEAT is taken as a true statement then:

Illustration of proof of the HSEAT Triangle somme des angles.png
Illustration of proof of the HSEAT

Proving that the sum of the measures of the angles of a triangle is 180°.

The Euclidean proof of the HSEAT (and simultaneously the result on the sum of the angles of a triangle) starts by constructing the line parallel to side AB passing through point C and then using the properties of corresponding angles and alternate interior angles of parallel lines to get the conclusion as in the illustration. [9]

The HSEAT can be extremely useful when trying to calculate the measures of unknown angles in a triangle.

Notes

  1. ↑ Henderson & Taimiņa 2005 , p. 110
  2. ↑ Wylie, Jr. 1964 , p. 101 & p. 106
  3. ↑ One line segment is considered the initial side and the other the terminal side. The angle is formed by going counterclockwise from the initial side to the terminal side. The choice of which line segment is the initial side is arbitrary, so there are two possibilities for the angle determined by the line segments.
  4. ↑ This way of defining interior angles does not presuppose that the sum of the angles of a triangle is 180 degrees.
  5. ↑ Faber 1983 , p. 113
  6. ↑ Greenberg 1974 , p. 99
  7. ↑ Venema 2006 , p. 10
  8. ↑ Greenberg 1974 , p. 99
  9. ↑ Heath 1956 , Vol. 1, p. 316

Related Research Articles

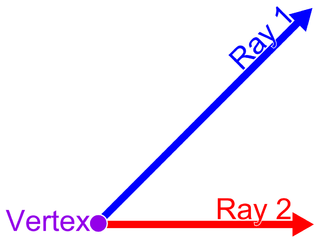
Angle Figure formed by two rays meeting at a common point

In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in the plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.

Euclidean geometry Mathematical model of the physical space

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates), and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

Triangle Shape with three sides

A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

Congruence (geometry) Relationship between two figures of the same shape and size, or mirroring each other

In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.

Similarity (geometry) Same shape, up to a scaling

In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

Cyclic quadrilateral Quadrilateral whose vertices can all fall on a single circle

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

Thaless theorem Angle formed by a point on a circle and the 2 ends of a diameter is a right angle

In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

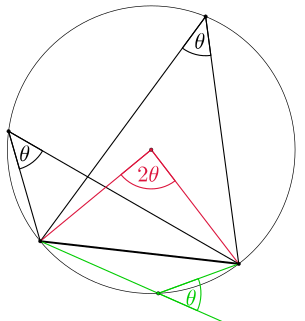
Inscribed angle

In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle.

Absolute geometry Geometry without the parallel postulate

Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates, but since these are not sufficient as a basis of Euclidean geometry, other systems, such as Hilbert's axioms without the parallel axiom, are used. The term was introduced by János Bolyai in 1832. It is sometimes referred to as neutral geometry, as it is neutral with respect to the parallel postulate.

Morleys trisector theorem 3 intersections of any triangles adjacent angle trisectors form an equilateral triangle

In plane geometry, Morley's trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the first Morley triangle or simply the Morley triangle. The theorem was discovered in 1899 by Anglo-American mathematician Frank Morley. It has various generalizations; in particular, if all of the trisectors are intersected, one obtains four other equilateral triangles.

Hyperbolic triangle Triangle in hyperbolic geometry

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.

Special right triangle Right triangle with a feature making calculations on the triangle easier

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.

Angle bisector theorem On the relative lengths of two segments that divide a triangle

In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

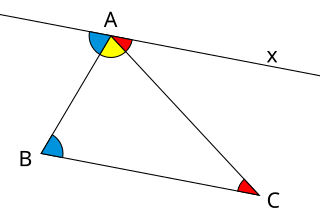
Sum of angles of a triangle

In a Euclidean space, the sum of angles of a triangle equals the straight angle . A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.

Transversal (geometry) Line intersecting 2 coplanar lines at 2 points

In geometry, a transversal is a line that passes through two lines in the same plane at two distinct points. Transversals play a role in establishing whether two or more other lines in the Euclidean plane are parallel. The intersections of a transversal with two lines create various types of pairs of angles: consecutive interior angles, consecutive exterior angles, corresponding angles, and alternate angles. As a consequence of Euclid's parallel postulate, if the two lines are parallel, consecutive interior angles are supplementary, corresponding angles are equal, and alternate angles are equal.

Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

Pythagorean theorem Relation between sides of a right triangle

In mathematics, the Pythagorean theorem, or Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the legs a, b and the hypotenuse c, often called the Pythagorean equation:

Playfairs axiom Modern formulation of Euclids parallel postulate

In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid :

In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.

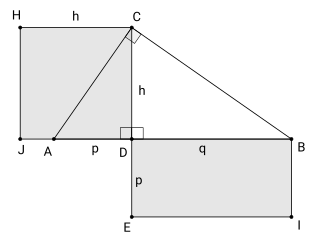
Geometric mean theorem Relates the altitude on the hypotenuse in a right triangle and the 2 line segments created

The right triangle altitude theorem or geometric mean theorem is a result in elementary geometry that describes a relation between the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. It states that the geometric mean of the two segments equals the altitude.

In Euclidean geometry, the trillium theorem – is a statement about properties of inscribed and circumscribed circles and their relations.

References

(3 vols.): ISBN   0-486-60088-2 (vol. 1), ISBN   0-486-60089-0 (vol. 2), ISBN   0-486-60090-4 (vol. 3).

HSEAT references

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.