Geometric mean theorem

area of grey square = area of grey rectangle: ${\displaystyle h^{2}=pq\Leftrightarrow h={\sqrt {pq}}}$

In Euclidean geometry, the right triangle altitude theorem or geometric mean theorem is a relation between the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. It states that the geometric mean of the two segments equals the altitude.

Theorem and applications

Construction of ${\displaystyle {\sqrt {p}}}$ by setting q to 1

If h denotes the altitude in a right triangle and p and q the segments on the hypotenuse then the theorem can be stated as: ^[1]

${\displaystyle h={\sqrt {pq}}}$

or in term of areas:

${\displaystyle h^{2}=pq.}$

AM-GM inequality

The latter version yields a method to square a rectangle with ruler and compass, that is to construct a square of equal area to a given rectangle. For such a rectangle with sides p and q we denote its top left vertex with D. Now we extend the segment q to its left by p (using arc AE centered on D) and draw a half circle with endpoints A and B with the new segment p + q as its diameter. Then we erect a perpendicular line to the diameter in D that intersects the half circle in C. Due to Thales' theorem C and the diameter form a right triangle with the line segment DC as its altitude, hence DC is the side of a square with the area of the rectangle. The method also allows for the construction of square roots (see constructible number), since starting with a rectangle that has a width of 1 the constructed square will have a side length that equals the square root of the rectangle's length. ^[1]

Another application of provides a geometrical proof of the AM–GM inequality in the case of two numbers. For the numbers p and q one constructs a half circle with diameter p + q. Now the altitude represents the geometric mean and the radius the arithmetic mean of the two numbers. Since the altitude is always smaller or equal to the radius, this yields the inequality. ^[2]

geometric mean theorem as a special case of the chord theorem:
${\displaystyle |CD||DE|=|AD||DB|\Leftrightarrow h^{2}=pq}$

The theorem can also be thought of as a special case of the intersecting chords theorem for a circle, since the converse of Thales' theorem ensures that the hypotenuse of the right angled triangle is the diameter of its circumcircle. ^[1]

The converse statement is true as well. Any triangle, in which the altitude equals the geometric mean of the two line segments created by it, is a right triangle.

History

The theorem is usually attributed to Euclid (ca. 360–280 BC), who stated it as a corollary to proposition 8 in book VI of his Elements. In proposition 14 of book II Euclid gives a method for squaring a rectangle, which essentially matches the method given here. Euclid however provides a different slightly more complicated proof for the correctness of the construction rather than relying on the geometric mean theorem. ^{[1] [3]}

Proof

Based on similarity

${\displaystyle \triangle ABC\sim \triangle ADC\sim \triangle DBC}$

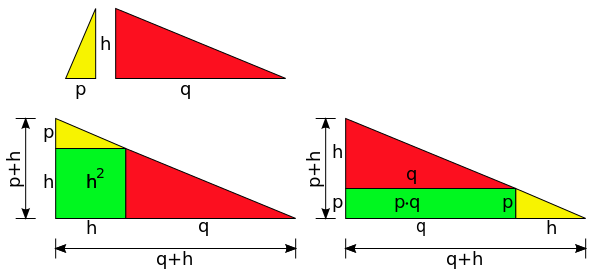
Proof of theorem:

The triangles △ADC , △ BCD are similar, since:

• consider triangles △ABC, △ACD; here we have
  $${\displaystyle \angle ACB=\angle ADC=90^{\circ },\quad \angle BAC=\angle CAD;}$$
  therefore by the AA postulate
  $${\displaystyle \triangle ABC\sim \triangle ACD.}$$
• further, consider triangles △ABC, △BCD; here we have
  $${\displaystyle \angle ACB=\angle BDC=90^{\circ },\quad \angle ABC=\angle CBD;}$$
  therefore by the AA postulate
  $${\displaystyle \triangle ABC\sim \triangle BCD.}$$

Therefore, both triangles △ACD, △BCD are similar to △ABC and themselves, i.e.

$${\displaystyle \triangle ACD\sim \triangle ABC\sim \triangle BCD.}$$

Because of the similarity we get the following equality of ratios and its algebraic rearrangement yields the theorem: ^[1]

${\displaystyle {\frac {h}{p}}={\frac {q}{h}}\,\Leftrightarrow \,h^{2}=pq\,\Leftrightarrow \,h={\sqrt {pq}}\qquad (h,p,q>0)}$

Proof of converse:

For the converse we have a triangle △ABC in which ${\displaystyle h^{2}=pq}$ holds and need to show that the angle at C is a right angle. Now because of ${\displaystyle h^{2}=pq}$ we also have ${\displaystyle {\tfrac {h}{p}}={\tfrac {q}{h}}.}$ Together with ${\displaystyle \angle ADC=\angle CDB}$ the triangles △ADC, △BDC have an angle of equal size and have corresponding pairs of legs with the same ratio. This means the triangles are similar, which yields:

${\displaystyle {\begin{aligned}\angle ACB&=\angle ACD+\angle DCB\\&=\angle ACD+(90^{\circ }-\angle DBC)\\&=\angle ACD+(90^{\circ }-\angle ACD)\\&=90^{\circ }\end{aligned}}}$

Based on the Pythagorean theorem

Proof with the Pythagorean theorem

In the setting of the geometric mean theorem there are three right triangles △ABC, △ADC and △DBC in which the Pythagorean theorem yields:

${\displaystyle {\begin{aligned}h^{2}&=a^{2}-q^{2}\\h^{2}&=b^{2}-p^{2}\\c^{2}&=a^{2}+b^{2}\end{aligned}}}$

Adding the first 2 two equations and then using the third then leads to:

${\displaystyle {\begin{aligned}2h^{2}&=a^{2}+b^{2}-p^{2}-q^{2}\\&=c^{2}-p^{2}-q^{2}\\&=(p+q)^{2}-p^{2}-q^{2}\\&=2pq\\\therefore \ h^{2}&=pq.\end{aligned}}}$

which finally yields the formula of the geometric mean theorem. ^[4]

Based on dissection and rearrangement

Dissecting the right triangle along its altitude h yields two similar triangles, which can be augmented and arranged in two alternative ways into a larger right triangle with perpendicular sides of lengths p + h and q + h. One such arrangement requires a square of area h² to complete it, the other a rectangle of area pq. Since both arrangements yield the same triangle, the areas of the square and the rectangle must be identical.

Based on shear mappings

The square of the altitude can be transformed into an rectangle of equal area with sides p and q with the help of three shear mappings (shear mappings preserve the area):

Shear mappings with their associated fixed lines (dotted), starting with the original square as preimage each parallelogram displays the image of a shear mapping of the figure left of it

References

1. • Hartmut Wellstein, Peter Kirsche: Elementargeometrie. Springer, 2009, ISBN   9783834808561, pp. 76-77 (German, online copy , p. 76, at Google Books)
2. Claudi Alsina, Roger B. Nelsen: Icons of Mathematics: An Exploration of Twenty Key Images . MAA 2011, ISBN   9780883853528, pp. 31–32 ( online copy , p. 31, at Google Books)
3. Euclid: Elements, book II – prop. 14, book VI – pro6767800hshockedmake ,me uoppppp. 8, (online copy)
4. Ilka Agricola, Thomas Friedrich: Elementary Geometry. AMS 2008, ISBN   9780821843475, p. 25 ( online copy , p. 25, at Google Books)

External links

• Geometric Mean at Cut-the-Knot