Hypotenuse

A right-angled triangle and its hypotenuse

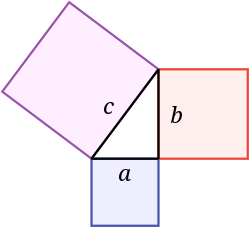
In geometry, a hypotenuse is the side of a right triangle that is opposite to the right angle. ^[1] It is always the longest side of the triangle. The other two sides of a right triangle are called legs or catheti. ^{[2] [3]}

The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. As an algebraic formula, this can be written as ${\displaystyle a^{2}+b^{2}=c^{2}}$, where ⁠${\displaystyle a}$⁠ is the length of one leg, ⁠${\displaystyle b}$⁠ is the length of the other leg, and ⁠${\displaystyle c}$⁠ is the length of the hypotenuse. ^[4] For example, if the two legs of a right triangle have lengths 3 and 4, respectively, then the hypotenuse has length 5, because ⁠${\displaystyle \textstyle 3^{2}+4^{2}=25=5^{2}}$⁠. ^[2]

Etymology

The English word hypotenuse is derived from the Greek word hypoteinousa (ὑποτείνουσα), which means "stretching under". It refers to how the hypotenuse "stretches under" the right angle. ^{[5] [6]}

Plato used the word in the 4th century BCE. ^[7] It was loaned into Latin as hypotenusa and later into French as hypoténuse. ^[8] It first appeared in English in the 1570s. ^[5]

Properties

Pythagorean theorem

An illustration of the Pythagorean theorem

Main article: Pythagorean theorem

The Pythagorean theorem states that the square of the length of the hypotenuse (⁠${\displaystyle c}$⁠) is equal to the sum of the squares of the lengths of the other two sides (⁠${\displaystyle a}$⁠ and ⁠${\displaystyle b}$⁠). This can be written as the equation ⁠${\displaystyle a^{2}+b^{2}=c^{2}}$⁠. To calculate the length of the hypotenuse, the equation can be rearranged to solve for ⁠${\displaystyle c}$⁠ by taking the square root of both sides, yielding ⁠${\displaystyle c={\sqrt {a^{2}+b^{2}}}}$⁠. This is sometimes known as Pythagorean addition. ^[9] For example, if the two legs of a right triangle have lengths 3 and 4, respectively, then the hypotenuse has length 5, because ⁠${\displaystyle {\sqrt {3^{2}+4^{2}}}={\sqrt {25}}=5}$⁠. ^[2]

The Pythagorean theorem is a special case of the law of cosines, a more general theorem relating the lengths of sides in any triangle. It states that ⁠${\displaystyle a^{2}+b^{2}-2ab\cos {\theta }=c^{2}}$⁠ where ⁠${\displaystyle \theta }$⁠ is the angle between sides ⁠${\displaystyle a}$⁠ and ⁠${\displaystyle b}$⁠. ^[10] When ⁠${\displaystyle \theta }$⁠ is ⁠${\displaystyle {\tfrac {\pi }{2}}}$⁠ radians or 90°, then ⁠${\displaystyle \cos {\theta }=0}$⁠ and the formula reduces to the usual Pythagorean theorem.

Sine and cosine

For the angle α, the sine function gives the ratio of the length of the opposite side to the length of the hypotenuse.

Main article: Sine and cosine

The sine and cosine functions (sin and cos) describe the relationship of the hypotenuse to the lengths and angles of the other two sides. These, along with tangent (tan), are the most common trigonometric functions. ^[2]

The trig functions are usually described in terms of one of the acute angles of a right triangle (⁠${\displaystyle \angle A}$⁠), the leg that is adjacent to that angle, and the leg that is opposite that angle. The sine of the acute angle gives the ratio of the opposite leg to the hypotenuse, while the cosine of the angle gives the ratio of the adjacent leg to the hypotenuse. This can be written as the equations: $${\displaystyle \sin(\angle A)={\frac {\text{opposite}}{\text{hypotenuse}}},\qquad \cos(\angle A)={\frac {\text{adjacent}}{\text{hypotenuse}}}.}$$

The definitions of the sine, cosine and tangent functions are often remembered using the mnemonic "SOH-CAH-TOA", where "SOH" stands for "sine = opposite / hypotenuse", "CAH" stands for "cosine = adjacent / hypotenuse", and "TOA" stands for "tangent = opposite / adjacent". ^[2]

In computer programming

Many programming languages support a version of the ISO C standard function hypot(x, y), which calculates the hypotenuse of a right triangle using the Pythagorean theorem. ^{[11] [12] [13]} The function is designed not to fail where the straightforward calculation might overflow or underflow. It can often be more accurate and slower than the straightforward calculation. ^[9]

Some languages have extended the definition to higher dimensions. For example, C++17 supports std::hypot(x, y, z) which gives the length of the diagonal of a rectangular cuboid with edge lengths x, y, and z. ^[14] Python 3.8 includes a version of math.hypot which can handle an arbitrary number of arguments. ^[15]

See also

• Mathematics portal

• Cathetus
• Triangle
• Space diagonal
• Nonhypotenuse number
• Taxicab geometry
• Trigonometry
• Special right triangles
• Pythagoras
• Norm_(mathematics)#Euclidean_norm

Notes

1. "Triangle (geometry)"  . Encyclopædia Britannica . Vol. 27 (11th ed.). 1911. p. 258. ...Also a right-angled triangle has one angle a right angle, the side opposite this angle being called the hypotenuse;...
2. Africk, Henry (2021). Elementary College Geometry (2021 ed.). New York City College of Technology.
3. Weisstein, Eric W. "Cathetus". MathWorld. Wolfram Research. Retrieved 2025-12-17.
4. Moland Jr, Jesse (August 2009). I Hate Trig!: A Practical Guide to Understanding Trigonometry. Jesse Moland. p. 1. ISBN   978-1-4486-4707-1.
5. "hypotenuse". Online Etymology Dictionary. Retrieved 2019-05-14.
6. "hypotenuse definition and word origin". Collins Dictionary. Collins. Retrieved 2022-04-12.
7. Plato; Jowett, Benjamin (1871). Timaeus (Jowett)  – via Wikisource.
8. "Hypotenuse". CNRTL (in French). Retrieved 2025-12-17.
9. Moler, Cleve; Morrison, Donald (1983). "Replacing square roots by Pythagorean sums". IBM Journal of Research and Development. 27 (6): 577–581. CiteSeerX   10.1.1.90.5651 . doi:10.1147/rd.276.0577.
10. Leff, Lawrence S. (2005-05-01). PreCalculus the Easy Way. Barron's Educational Series. p. 326. ISBN   0-7641-2892-2.
11. "hypot(3)". Linux Programmer's Manual. Retrieved 4 December 2021.
12. Horton, Ivor (2005). Ivor Horton's Beginning Java 2. John Wiley & Sons. p. 57. ISBN   9780764568749.
13. Hill, Christian (2020). Learning Scientific Programming with Python (2nd ed.). Cambridge University Press. p. 14. ISBN   9781108787468.
14. "C++ std::hypot". C++ Language Manual. Retrieved 6 June 2024.
15. "Python math.hypot". Python Language Manual. Retrieved 6 June 2024.

References

• Hypotenuse at Encyclopaedia of Mathematics
• Weisstein, Eric W. "Hypotenuse". MathWorld .