
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.

In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.

In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
In geometry, a secant is a line that intersects a curve at a minimum of two distinct points. The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant intersects the circle at exactly two points. A chord is the line segment determined by the two points, that is, the interval on the secant whose ends are the two points.
In geometry, inversive geometry is the study of inversion, a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry become much more tractable when an inversion is applied. Inversion seems to have been discovered by a number of people contemporaneously, including Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs and Ingram (1842-3) and Kelvin (1845).

A chord of a circle is a straight line segment whose endpoints both lie on a circular arc. If a chord were to be extended infinitely on both directions into a line, the object is a secant line. The perpendicular line passing through the chord's midpoint is called sagitta.

Menelaus's theorem, named for Menelaus of Alexandria, is a proposition about triangles in plane geometry. Suppose we have a triangle ABC, and a transversal line that crosses BC, AC, and AB at points D, E, and F respectively, with D, E, and F distinct from A, B, and C. A weak version of the theorem states that

In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826.
The circles of Apollonius are any of several sets of circles associated with Apollonius of Perga, a renowned Greek geometer. Most of these circles are found in planar Euclidean geometry, but analogs have been defined on other surfaces; for example, counterparts on the surface of a sphere can be defined through stereographic projection.

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.
The intercept theorem, also known as Thales's theorem, basic proportionality theorem or side splitter theorem is an important theorem in elementary geometry about the ratios of various line segments that are created if two rays with a common starting point are intercepted by a pair of parallels. It is equivalent to the theorem about ratios in similar triangles. It is traditionally attributed to Greek mathematician Thales. It was known to the ancient Babylonians and Egyptians, although its first known proof appears in Euclid's Elements.
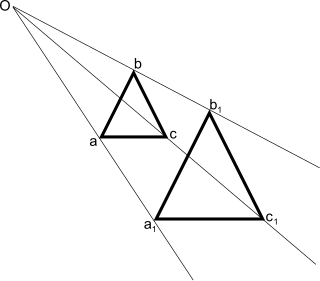
In geometry, a homothetic center is a point from which at least two geometrically similar figures can be seen as a dilation or contraction of one another. If the center is external, the two figures are directly similar to one another; their angles have the same rotational sense. If the center is internal, the two figures are scaled mirror images of one another; their angles have the opposite sense.

In Euclidean geometry, the intersecting chords theorem, or just the chord theorem, is a statement that describes a relation of the four line segments created by two intersecting chords within a circle. It states that the products of the lengths of the line segments on each chord are equal. It is Proposition 35 of Book 3 of Euclid's Elements.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:
In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.
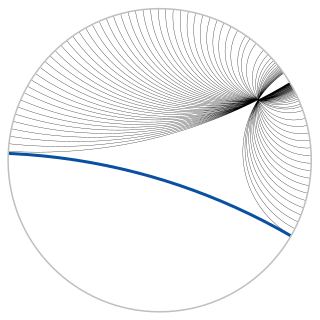
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.

In Euclidean geometry, the tangent-secant theorem describes the relation of line segments created by a secant and a tangent line with the associated circle. This result is found as Proposition 36 in Book 3 of Euclid's Elements.

Van Schooten's theorem, named after the Dutch mathematician Frans van Schooten, describes a property of equilateral triangles. It states:
![^
P
A
C
~
^
P
B
D
{\displaystyle \triangle PAC\sim \triangle PBD}
yields
|
P
A
|
[?]
|
P
D
|
=
|
P
B
|
[?]
|
P
C
|
{\displaystyle |PA|\cdot |PD|=|PB|\cdot |PC|} Secant theorem.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/4/48/Secant_theorem.svg/220px-Secant_theorem.svg.png)
















