Inverse Pythagorean theorem

Last updated July 28, 2024

Base Pytha- gorean triple	AC	BC	CD	AB
(3, 4, 5)	20 = 4× 5	15 = 3× 5	12 = 3× 4	25 = 5²
(5, 12, 13)	156 = 12×13	65 = 5×13	60 = 5×12	169 = 13²
(8, 15, 17)	255 = 15×17	136 = 8×17	120 = 8×15	289 = 17²
(7, 24, 25)	600 = 24×25	175 = 7×25	168 = 7×24	625 = 25²
(20, 21, 29)	609 = 21×29	580 = 20×29	420 = 20×21	841 = 29²
All positive integer primitive inverse-Pythagorean triples having up to three digits, with the hypotenuse for comparison

In geometry, the inverse Pythagorean theorem (also known as the reciprocal Pythagorean theorem^[1] or the upside down Pythagorean theorem^[2]) is as follows:^[3]

Proof

The area of triangle $△ ABC$ can be expressed in terms of either $AC$ and $BC$ , or $AB$ and $CD$ :

{\begin{aligned}{\tfrac {1}{2}}AC\cdot BC&={\tfrac {1}{2}}AB\cdot CD\\[4pt](AC\cdot BC)^{2}&=(AB\cdot CD)^{2}\\[4pt]{\frac {1}{CD^{2}}}&={\frac {AB^{2}}{AC^{2}\cdot BC^{2}}}\end{aligned}}

given $CD > 0$ , $AC > 0$ and $BC > 0$ .

Using the Pythagorean theorem,

{\begin{aligned}{\frac {1}{CD^{2}}}&={\frac {BC^{2}+AC^{2}}{AC^{2}\cdot BC^{2}}}\\[4pt]&={\frac {BC^{2}}{AC^{2}\cdot BC^{2}}}+{\frac {AC^{2}}{AC^{2}\cdot BC^{2}}}\\[4pt]\quad \therefore \;\;{\frac {1}{CD^{2}}}&={\frac {1}{AC^{2}}}+{\frac {1}{BC^{2}}}\end{aligned}}

as above.

Note in particular:

{\begin{aligned}{\tfrac {1}{2}}AC\cdot BC&={\tfrac {1}{2}}AB\cdot CD\\[4pt]CD&={\tfrac {AC\cdot BC}{AB}}\\[4pt]\end{aligned}}

Special case of the cruciform curve

The cruciform curve or cross curve is a quartic plane curve given by the equation

x^{2}y^{2}-b^{2}x^{2}-a^{2}y^{2}=0

where the two parameters determining the shape of the curve, $a$ and $b$ are each $CD$ .

Substituting $x$ with $AC$ and $y$ with $BC$ gives

{\begin{aligned}AC^{2}BC^{2}-CD^{2}AC^{2}-CD^{2}BC^{2}&=0\\[4pt]AC^{2}BC^{2}&=CD^{2}BC^{2}+CD^{2}AC^{2}\\[4pt]{\frac {1}{CD^{2}}}&={\frac {BC^{2}}{AC^{2}\cdot BC^{2}}}+{\frac {AC^{2}}{AC^{2}\cdot BC^{2}}}\\[4pt]\therefore \;\;{\frac {1}{CD^{2}}}&={\frac {1}{AC^{2}}}+{\frac {1}{BC^{2}}}\end{aligned}}

Inverse-Pythagorean triples can be generated using integer parameters $t$ and $u$ as follows.^[4]

{\begin{aligned}AC&=(t^{2}+u^{2})(t^{2}-u^{2})\\BC&=2tu(t^{2}+u^{2})\\CD&=2tu(t^{2}-u^{2})\end{aligned}}

Application

If two identical lamps are placed at $A$ and $B$ , the theorem and the inverse-square law imply that the light intensity at $C$ is the same as when a single lamp is placed at $D$ .

Related Research Articles

A Pythagorean triple consists of three positive integers $a$ , $b$ , and $c$ , such that $a 2 + b 2 = c 2$ . Such a triple is commonly written $(a, b, c)$ , a well-known example is $(3, 4, 5)$ . If $(a, b, c)$ is a Pythagorean triple, then so is $(ka, kb, kc)$ for any positive integer $k$ . A triangle whose side lengths are a Pythagorean triple is a right triangle and called a Pythagorean triangle.

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.

<span class="mw-page-title-main">Similarity (geometry)</span> Property of objects which are scaled or mirrored versions of each other

In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

<span class="mw-page-title-main">Right triangle</span> Triangle containing a 90-degree angle

A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular forming a right angle.

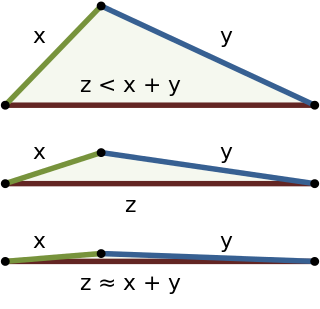
<span class="mw-page-title-main">Triangle inequality</span> Property of geometry, also used to generalize the notion of "distance" in metric spaces

In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If $a$ , $b$ , and $c$ are the lengths of the sides of a triangle then the triangle inequality states that

<span class="mw-page-title-main">Altitude (triangle)</span> Perpendicular line segment from a triangles side to opposite vertex

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the side opposite the vertex. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

In geometry, Thales's theorem states that if $A$ , $B$ , and $C$ are distinct points on a circle where the line $AC$ is a diameter, the angle $∠ ABC$ is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

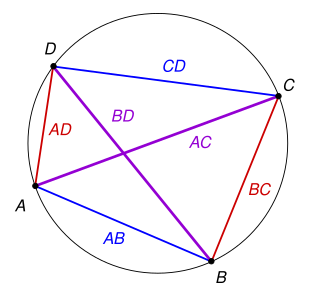
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.

In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation:

In Euclidean geometry, the British flag theorem says that if a point P is chosen inside a rectangle ABCD then the sum of the squares of the Euclidean distances from P to two opposite corners of the rectangle equals the sum to the other two opposite corners. As an equation:

In mathematics, Pythagorean addition is a binary operation on the real numbers that computes the length of the hypotenuse of a right triangle, given its two sides. According to the Pythagorean theorem, for a triangle with sides $and, this length can be calculated as$

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides $and opposite respective angles and, the law of cosines states:$

<span class="mw-page-title-main">Snellius–Pothenot problem</span> Problem in trigonometry

In trigonometry, the Snellius–Pothenot problem is a problem first described in the context of planar surveying. Given three known points $A, B, C$ , an observer at an unknown point $P$ observes that the line segment $AC$ subtends an angle $α$ and the segment $CB$ subtends an angle $β$ ; the problem is to determine the position of the point $P$ ..

<span class="mw-page-title-main">Pythagorean theorem</span> Relation between sides of a right triangle

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

<span class="mw-page-title-main">Integer triangle</span> Triangle with integer side lengths

An integer triangle or integral triangle is a triangle all of whose side lengths are integers. A rational triangle is one whose side lengths are rational numbers; any rational triangle can be rescaled by the lowest common denominator of the sides to obtain a similar integer triangle, so there is a close relationship between integer triangles and rational triangles.

<span class="mw-page-title-main">Geometric mean theorem</span> Theorem about right triangles

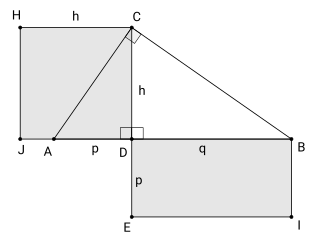
In Euclidean geometry, the geometric mean theorem or right triangle altitude theorem is a relation between the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. It states that the geometric mean of the two segments equals the altitude.

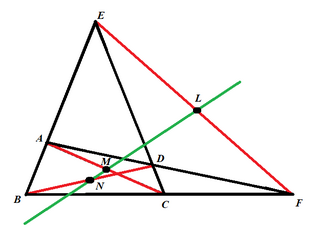
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrilateral.

References

↑ R. B. Nelsen, Proof Without Words: A Reciprocal Pythagorean Theorem, Mathematics Magazine, 82, December 2009, p. 370
↑ The upside-down Pythagorean theorem, Jennifer Richinick, The Mathematical Gazette, Vol. 92, No. 524 (July 2008), pp. 313-316
↑ Johan Wästlund, "Summing inverse squares by euclidean geometry", http://www.math.chalmers.se/~wastlund/Cosmic.pdf, pp. 4–5.
↑ "Diophantine equation of three variables".

This geometry-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] R. B. Nelsen, Proof Without Words: A Reciprocal Pythagorean Theorem, Mathematics Magazine, 82, December 2009, p. 370

[2] The upside-down Pythagorean theorem, Jennifer Richinick, The Mathematical Gazette, Vol. 92, No. 524 (July 2008), pp. 313-316

[3] Johan Wästlund, "Summing inverse squares by euclidean geometry", http://www.math.chalmers.se/~wastlund/Cosmic.pdf, pp. 4–5.

[4] "Diophantine equation of three variables".

[1]

[2]

[3]

[4]