In mathematics, an Abel equation of the first kind, named after Niels Henrik Abel, is any ordinary differential equation that is cubic in the unknown function. In other words, it is an equation of the form
Contents
where .
In mathematics, an Abel equation of the first kind, named after Niels Henrik Abel, is any ordinary differential equation that is cubic in the unknown function. In other words, it is an equation of the form
where .
If and , or and , the equation reduces to a Bernoulli equation, while if the equation reduces to a Riccati equation.
The substitution brings the Abel equation of the first kind to the Abel equation of the second kind, of the form
The substitution
brings the Abel equation of the first kind to the canonical form
Dimitrios E. Panayotounakos and Theodoros I. Zarmpoutis discovered an analytic method to solve the above equation in an implicit form. [1]

Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation

In physics, engineering and mathematics, the Fourier transform (FT) is an integral transform that takes a function as input and outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches.
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.
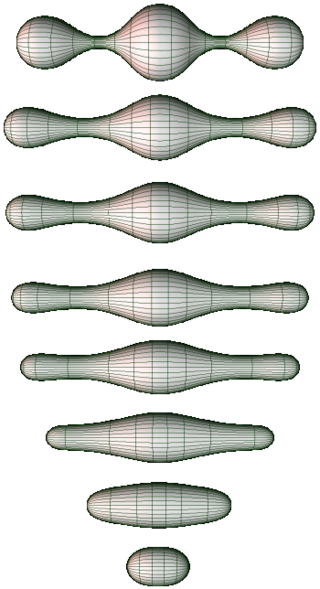
In the mathematical fields of differential geometry and geometric analysis, the Ricci flow, sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation.
Functional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions. Functional integrals arise in probability, in the study of partial differential equations, and in the path integral approach to the quantum mechanics of particles and fields.

In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation.

In the physical sciences, the Airy function (or Airy function of the first kind) Ai(x) is a special function named after the British astronomer George Biddell Airy (1801–1892). The function Ai(x) and the related function Bi(x), are linearly independent solutions to the differential equation
In mathematics, integral equations are equations in which an unknown function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form:
In mathematics and its applications, a Sturm–Liouville problem is a second-order linear ordinary differential equation of the form:
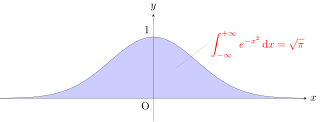
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic and parabolic partial differential equation. The method is to reduce a partial differential equation to a family of ordinary differential equations along which the solution can be integrated from some initial data given on a suitable hypersurface.

Burgers' equation or Bateman–Burgers equation is a fundamental partial differential equation and convection–diffusion equation occurring in various areas of applied mathematics, such as fluid mechanics, nonlinear acoustics, gas dynamics, and traffic flow. The equation was first introduced by Harry Bateman in 1915 and later studied by Johannes Martinus Burgers in 1948. For a given field and diffusion coefficient , the general form of Burgers' equation in one space dimension is the dissipative system:

In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.
In mathematics, constraint counting is counting the number of constraints in order to compare it with the number of variables, parameters, etc. that are free to be determined, the idea being that in most cases the number of independent choices that can be made is the excess of the latter over the former.
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.
An -superprocess, , within mathematics probability theory is a stochastic process on that is usually constructed as a special limit of near-critical branching diffusions.

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are called cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.
In mathematics, the slow manifold of an equilibrium point of a dynamical system occurs as the most common example of a center manifold. One of the main methods of simplifying dynamical systems, is to reduce the dimension of the system to that of the slow manifold—center manifold theory rigorously justifies the modelling. For example, some global and regional models of the atmosphere or oceans resolve the so-called quasi-geostrophic flow dynamics on the slow manifold of the atmosphere/oceanic dynamics, and is thus crucial to forecasting with a climate model.

The Peregrine soliton is an analytic solution of the nonlinear Schrödinger equation. This solution was proposed in 1983 by Howell Peregrine, researcher at the mathematics department of the University of Bristol.