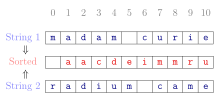In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. A simpler example is equality. Any number is equal to itself (reflexive). If , then (symmetric). If and , then (transitive).

In mathematics, when the elements of some set have a notion of equivalence, then one may naturally split the set into equivalence classes. These equivalence classes are constructed so that elements and belong to the same equivalence class if, and only if, they are equivalent.

In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is derived from Ancient Greek ἴσος (isos) 'equal' and μορφή (morphe) 'form, shape'.
In logic and computer science, specifically automated reasoning, unification is an algorithmic process of solving equations between symbolic expressions, each of the form Left-hand side = Right-hand side. For example, using x,y,z as variables, and taking f to be an uninterpreted function, the singleton equation set { f(1,y) = f(x,2) } is a syntactic first-order unification problem that has the substitution { x ↦ 1, y ↦ 2 } as its only solution.

In mathematics, equality is a relationship between two quantities or expressions, stating that they have the same value, or represent the same mathematical object. Equality between A and B is written A = B, and pronounced "A equals B". In this equality, A and B are distinguished by calling them left-hand side (LHS), and right-hand side (RHS). Two objects that are not equal are said to be distinct.

In geometry, a geodesic is a curve representing in some sense the locally shortest path (arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line".
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not vary smoothly in this way, but have distinct, separated values. Discrete mathematics, therefore, excludes topics in "continuous mathematics" such as calculus and analysis.
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems. In their most basic form, they consist of a set of objects, plus relations on how to transform those objects.

In mathematics, an expression is a written arrangement of symbols following the context-dependent, syntactic conventions of mathematical notation. Symbols can denote numbers, variables, operations, and functions. Other symbols include punctuation marks and brackets, used for grouping where there is not a well-defined order of operations.
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. In other cases the dual of the dual – the double dual or bidual – is not necessarily identical to the original. Such involutions sometimes have fixed points, so that the dual of A is A itself. For example, Desargues' theorem is self-dual in this sense under the standard duality in projective geometry.
The language of mathematics has a wide vocabulary of specialist and technical terms. It also has a certain amount of jargon: commonly used phrases which are part of the culture of mathematics, rather than of the subject. Jargon often appears in lectures, and sometimes in print, as informal shorthand for rigorous arguments or precise ideas. Much of this uses common English words, but with a specific non-obvious meaning when used in a mathematical sense.

In computer science and mathematics, confluence is a property of rewriting systems, describing which terms in such a system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.
In mathematics, a classification theorem answers the classification problem: "What are the objects of a given type, up to some equivalence?". It gives a non-redundant enumeration: each object is equivalent to exactly one class.
In abstract rewriting, an object is in normal form if it cannot be rewritten any further, i.e. it is irreducible. Depending on the rewriting system, an object may rewrite to several normal forms or none at all. Many properties of rewriting systems relate to normal forms.
In mathematics, in the theory of rewriting systems, Newman's lemma, also commonly called the diamond lemma, states that a terminating abstract rewriting system (ARS), that is, one in which there are no infinite reduction sequences, is confluent if it is locally confluent. In fact a terminating ARS is confluent precisely when it is locally confluent.
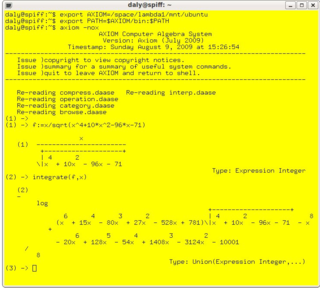
In mathematics and computer science, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions and other mathematical objects. Although computer algebra could be considered a subfield of scientific computing, they are generally considered as distinct fields because scientific computing is usually based on numerical computation with approximate floating point numbers, while symbolic computation emphasizes exact computation with expressions containing variables that have no given value and are manipulated as symbols.
In mathematical logic and theoretical computer science, an abstract rewriting system is a formalism that captures the quintessential notion and properties of rewriting systems. In its simplest form, an ARS is simply a set together with a binary relation, traditionally denoted with ; this definition can be further refined if we index (label) subsets of the binary relation. Despite its simplicity, an ARS is sufficient to describe important properties of rewriting systems like normal forms, termination, and various notions of confluence.
In mathematical logic, a term denotes a mathematical object while a formula denotes a mathematical fact. In particular, terms appear as components of a formula. This is analogous to natural language, where a noun phrase refers to an object and a whole sentence refers to a fact.
In computer science, algebraic semantics is a form of axiomatic semantics based on algebraic laws for describing and reasoning about program specifications in a formal manner.