Weyr canonical form

The image shows an example of a general Weyr matrix consisting of two blocks each of which is a basic Weyr matrix. The basic Weyr matrix in the top-left corner has the structure (4,2,1) and the other one has the structure (2,2,1,1).

In mathematics, in linear algebra, a Weyr canonical form (or, Weyr form or Weyr matrix) is a square matrix which (in some sense) induces "nice" properties with matrices it commutes with. It also has a particularly simple structure and the conditions for possessing a Weyr form are fairly weak, making it a suitable tool for studying classes of commuting matrices. A square matrix is said to be in the Weyr canonical form if the matrix has the structure defining the Weyr canonical form. The Weyr form was discovered by the Czech mathematician Eduard Weyr in 1885. ^{[1] [2] [3]} The Weyr form did not become popular among mathematicians and it was overshadowed by the closely related, but distinct, canonical form known by the name Jordan canonical form. ^[3] The Weyr form has been rediscovered several times since Weyr’s original discovery in 1885. ^[4] This form has been variously called as modified Jordan form,reordered Jordan form,second Jordan form, and H-form. ^[4] The current terminology is credited to Shapiro who introduced it in a paper published in the American Mathematical Monthly in 1999. ^{[4] [5]}

Recently several applications have been found for the Weyr matrix. Of particular interest is an application of the Weyr matrix in the study of phylogenetic invariants in biomathematics.

Definitions

Definition

A basic Weyr matrix with eigenvalue ${\displaystyle \lambda }$ is an ${\displaystyle n\times n}$ matrix ${\displaystyle W}$ of the following form: There is an integer partition

${\displaystyle n_{1}+n_{2}+\cdots +n_{r}=n}$ of ${\displaystyle n}$ with ${\displaystyle n_{1}\geq n_{2}\geq \cdots \geq n_{r}\geq 1}$

such that, when ${\displaystyle W}$ is viewed as an ${\displaystyle r\times r}$ block matrix ${\displaystyle (W_{ij})}$, where the ${\displaystyle (i,j)}$ block ${\displaystyle W_{ij}}$ is an ${\displaystyle n_{i}\times n_{j}}$ matrix, the following three features are present:

1. The main diagonal blocks ${\displaystyle W_{ii}}$ are the ${\displaystyle n_{i}\times n_{i}}$ scalar matrices ${\displaystyle \lambda I}$ for ${\displaystyle i=1,\ldots ,r}$.
2. The first superdiagonal blocks ${\displaystyle W_{i,i+1}}$ are full column rank ${\displaystyle n_{i}\times n_{i+1}}$ matrices in reduced row-echelon form (that is, an identity matrix followed by zero rows) for ${\displaystyle i=1,\ldots ,r-1}$.
3. All other blocks of W are zero (that is, ${\displaystyle W_{ij}=0}$ when ${\displaystyle j\neq i,i+1}$).

In this case, we say that ${\displaystyle W}$ has Weyr structure ${\displaystyle (n_{1},n_{2},\ldots ,n_{r})}$.

Example

The following is an example of a basic Weyr matrix.

${\displaystyle W=}$ ${\displaystyle ={\begin{bmatrix}W_{11}&W_{12}&&\\&W_{22}&W_{23}&\\&&W_{33}&W_{34}\\&&&W_{44}\\\end{bmatrix}}}$

In this matrix, ${\displaystyle n=9}$ and ${\displaystyle n_{1}=4,n_{2}=2,n_{3}=2,n_{4}=1}$. So ${\displaystyle W}$ has the Weyr structure ${\displaystyle (4,2,2,1)}$. Also,

${\displaystyle W_{11}={\begin{bmatrix}\lambda &0&0&0\\0&\lambda &0&0\\0&0&\lambda &0\\0&0&0&\lambda \\\end{bmatrix}}=\lambda I_{4},\quad W_{22}={\begin{bmatrix}\lambda &0\\0&\lambda &\\\end{bmatrix}}=\lambda I_{2},\quad W_{33}={\begin{bmatrix}\lambda &0\\0&\lambda &\\\end{bmatrix}}=\lambda I_{2},\quad W_{44}={\begin{bmatrix}\lambda \\\end{bmatrix}}=\lambda I_{1}}$

and

${\displaystyle W_{12}={\begin{bmatrix}1&0\\0&1\\0&0\\0&0\\\end{bmatrix}},\quad W_{23}={\begin{bmatrix}1&0\\0&1\\\end{bmatrix}},\quad W_{34}={\begin{bmatrix}1\\0\\\end{bmatrix}}.}$

Definition

Let ${\displaystyle W}$ be a square matrix and let ${\displaystyle \lambda _{1},\ldots ,\lambda _{k}}$ be the distinct eigenvalues of ${\displaystyle W}$. We say that ${\displaystyle W}$ is in Weyr form (or is a Weyr matrix) if ${\displaystyle W}$ has the following form:

${\displaystyle W={\begin{bmatrix}W_{1}&&&\\&W_{2}&&\\&&\ddots &\\&&&W_{k}\\\end{bmatrix}}}$

where ${\displaystyle W_{i}}$ is a basic Weyr matrix with eigenvalue ${\displaystyle \lambda _{i}}$ for ${\displaystyle i=1,\ldots ,k}$.

Example

The following image shows an example of a general Weyr matrix consisting of three basic Weyr matrix blocks. The basic Weyr matrix in the top-left corner has the structure (4,2,1) with eigenvalue 4, the middle block has structure (2,2,1,1) with eigenvalue -3 and the one in the lower-right corner has the structure (3, 2) with eigenvalue 0.

Relation between Weyr and Jordan forms

The Weyr canonical form ${\displaystyle W=P^{-1}JP}$ is related to the Jordan form ${\displaystyle J}$ by a simple permutation ${\displaystyle P}$ for each Weyr basic block as follows: The first index of each Weyr subblock forms the largest Jordan chain. After crossing out these rows and columns, the first index of each new subblock forms the second largest Jordan chain, and so forth. ^[6]

The Weyr form is canonical

That the Weyr form is a canonical form of a matrix is a consequence of the following result: ^[3] Each square matrix ${\displaystyle A}$ over an algebraically closed field is similar to a Weyr matrix ${\displaystyle W}$ which is unique up to permutation of its basic blocks. The matrix ${\displaystyle W}$ is called the Weyr (canonical) form of ${\displaystyle A}$.

Computation of the Weyr canonical form

Reduction to the nilpotent case

Let ${\displaystyle A}$ be a square matrix of order ${\displaystyle n}$ over an algebraically closed field and let the distinct eigenvalues of ${\displaystyle A}$ be ${\displaystyle \lambda _{1},\lambda _{2},\ldots ,\lambda _{k}}$. The Jordan–Chevalley decomposition theorem states that ${\displaystyle A}$ is similar to a block diagonal matrix of the form

${\displaystyle A={\begin{bmatrix}\lambda _{1}I+N_{1}&&&\\&\lambda _{2}I+N_{2}&&\\&&\ddots &\\&&&\lambda _{k}I+N_{k}\\\end{bmatrix}}={\begin{bmatrix}\lambda _{1}I&&&\\&\lambda _{2}I&&\\&&\ddots &\\&&&\lambda _{k}I\\\end{bmatrix}}+{\begin{bmatrix}N_{1}&&&\\&N_{2}&&\\&&\ddots &\\&&&N_{k}\\\end{bmatrix}}=D+N}$

where ${\displaystyle D}$ is a diagonal matrix, ${\displaystyle N}$ is a nilpotent matrix, and ${\displaystyle [D,N]=0}$, justifying the reduction of ${\displaystyle N}$ into subblocks ${\displaystyle N_{i}}$. So the problem of reducing ${\displaystyle A}$ to the Weyr form reduces to the problem of reducing the nilpotent matrices ${\displaystyle N_{i}}$ to the Weyr form. This is leads to the generalized eigenspace decomposition theorem.

Reduction of a nilpotent matrix to the Weyr form

Given a nilpotent square matrix ${\displaystyle A}$ of order ${\displaystyle n}$ over an algebraically closed field ${\displaystyle F}$, the following algorithm produces an invertible matrix ${\displaystyle C}$ and a Weyr matrix ${\displaystyle W}$ such that ${\displaystyle W=C^{-1}AC}$.

Step 1

Let ${\displaystyle A_{1}=A}$

Step 2

1. Compute a basis for the null space of ${\displaystyle A_{1}}$.
2. Extend the basis for the null space of ${\displaystyle A_{1}}$ to a basis for the ${\displaystyle n}$-dimensional vector space ${\displaystyle F^{n}}$.
3. Form the matrix ${\displaystyle P_{1}}$ consisting of these basis vectors.
4. Compute ${\displaystyle P_{1}^{-1}A_{1}P_{1}={\begin{bmatrix}0&B_{2}\\0&A_{2}\end{bmatrix}}}$. ${\displaystyle A_{2}}$ is a square matrix of size ${\displaystyle n}$− nullity ${\displaystyle (A_{1})}$.

Step 3

If ${\displaystyle A_{2}}$ is nonzero, repeat Step 2 on ${\displaystyle A_{2}}$.

1. Compute a basis for the null space of ${\displaystyle A_{2}}$.
2. Extend the basis for the null space of ${\displaystyle A_{2}}$ to a basis for the vector space having dimension ${\displaystyle n}$− nullity ${\displaystyle (A_{1})}$.
3. Form the matrix ${\displaystyle P_{2}}$ consisting of these basis vectors.
4. Compute ${\displaystyle P_{2}^{-1}A_{2}P_{2}={\begin{bmatrix}0&B_{3}\\0&A_{3}\end{bmatrix}}}$. ${\displaystyle A_{2}}$ is a square matrix of size ${\displaystyle n}$− nullity ${\displaystyle (A_{1})}$− nullity${\displaystyle (A_{2})}$.

Step 4

Continue the processes of Steps 1 and 2 to obtain increasingly smaller square matrices ${\displaystyle A_{1},A_{2},A_{3},\ldots }$ and associated invertible matrices ${\displaystyle P_{1},P_{2},P_{3},\ldots }$ until the first zero matrix ${\displaystyle A_{r}}$ is obtained.

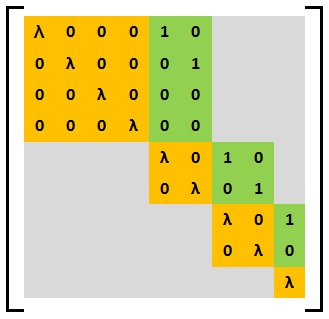
Step 5

The Weyr structure of ${\displaystyle A}$ is ${\displaystyle (n_{1},n_{2},\ldots ,n_{r})}$ where ${\displaystyle n_{i}}$ = nullity${\displaystyle (A_{i})}$.

Step 6

1. Compute the matrix ${\displaystyle P=P_{1}{\begin{bmatrix}I&0\\0&P_{2}\end{bmatrix}}{\begin{bmatrix}I&0\\0&P_{3}\end{bmatrix}}\cdots {\begin{bmatrix}I&0\\0&P_{r}\end{bmatrix}}}$ (here the ${\displaystyle I}$'s are appropriately sized identity matrices).
2. Compute ${\displaystyle X=P^{-1}AP}$. ${\displaystyle X}$ is a matrix of the following form:

${\displaystyle X={\begin{bmatrix}0&X_{12}&X_{13}&\cdots &X_{1,r-1}&X_{1r}\\&0&X_{23}&\cdots &X_{2,r-1}&X_{2r}\\&&&\ddots &\\&&&\cdots &0&X_{r-1,r}\\&&&&&0\end{bmatrix}}}$.

Step 7

Use elementary row operations to find an invertible matrix ${\displaystyle Y_{r-1}}$ of appropriate size such that the product ${\displaystyle Y_{r-1}X_{r,r-1}}$ is a matrix of the form ${\displaystyle I_{r,r-1}={\begin{bmatrix}I\\O\end{bmatrix}}}$.

Step 8

Set ${\displaystyle Q_{1}=}$ diag ${\displaystyle (I,I,\ldots ,Y_{r-1}^{-1},I)}$ and compute ${\displaystyle Q_{1}^{-1}XQ_{1}}$. In this matrix, the ${\displaystyle (r,r-1)}$-block is ${\displaystyle I_{r,r-1}}$.

Step 9

Find a matrix ${\displaystyle R_{1}}$ formed as a product of elementary matrices such that ${\displaystyle R_{1}^{-1}Q_{1}^{-1}XQ_{1}R_{1}}$ is a matrix in which all the blocks above the block ${\displaystyle I_{r,r-1}}$ contain only ${\displaystyle 0}$'s.

Step 10

Repeat Steps 8 and 9 on column ${\displaystyle r-1}$ converting ${\displaystyle (r-1,r-2)}$-block to ${\displaystyle I_{r-1,r-2}}$ via conjugation by some invertible matrix ${\displaystyle Q_{2}}$. Use this block to clear out the blocks above, via conjugation by a product ${\displaystyle R_{2}}$ of elementary matrices.

Step 11

Repeat these processes on ${\displaystyle r-2,r-3,\ldots ,3,2}$ columns, using conjugations by ${\displaystyle Q_{3},R_{3},\ldots ,Q_{r-2},R_{r-2},Q_{r-1}}$. The resulting matrix ${\displaystyle W}$ is now in Weyr form.

Step 12

Let ${\displaystyle C=P_{1}{\text{diag}}(I,P_{2})\cdots {\text{diag}}(I,P_{r-1})Q_{1}R_{1}Q_{2}\cdots R_{r-2}Q_{r-1}}$. Then ${\displaystyle W=C^{-1}AC}$.

Applications of the Weyr form

Some well-known applications of the Weyr form are listed below: ^[3]

1. The Weyr form can be used to simplify the proof of Gerstenhaber’s Theorem which asserts that the subalgebra generated by two commuting ${\displaystyle n\times n}$ matrices has dimension at most ${\displaystyle n}$.
2. A set of finite matrices is said to be approximately simultaneously diagonalizable if they can be perturbed to simultaneously diagonalizable matrices. The Weyr form is used to prove approximate simultaneous diagonalizability of various classes of matrices. The approximate simultaneous diagonalizability property has applications in the study of phylogenetic invariants in biomathematics.
3. The Weyr form can be used to simplify the proofs of the irreducibility of the variety of all k-tuples of commuting complex matrices.

References

1. Eduard Weyr (1885). "Répartition des matrices en espèces et formation de toutes les espèces" (PDF). Comptes Rendus de l'Académie des Sciences de Paris. 100: 966–969. Retrieved 10 December 2013.
2. Eduard Weyr (1890). "Zur Theorie der bilinearen Formen". Monatshefte für Mathematik und Physik. 1: 163–236.
3. Kevin C. Meara; John Clark; Charles I. Vinsonhaler (2011). Advanced Topics in Linear Algebra: Weaving Matrix Problems through the Weyr Form. Oxford University Press.
4. Kevin C. Meara; John Clark; Charles I. Vinsonhaler (2011). Advanced Topics in Linear Algebra: Weaving Matrix Problems through the Weyr Form. Oxford University Press. pp. 44, 81–82.
5. Shapiro, H. (1999). "The Weyr characteristic" (PDF). The American Mathematical Monthly. 106 (10): 919–929. doi:10.2307/2589746. JSTOR   2589746. S2CID   56072601.
6. Sergeichuk, "Canonical matrices for linear matrix problems", Arxiv:0709.2485 [math.RT], 2007