In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children. Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as databases and file systems.

In computing, a hash table, also known as hash map, is a data structure that implements an associative array or dictionary. It is an abstract data type that maps keys to values. A hash table uses a hash function to compute an index, also called a hash code, into an array of buckets or slots, from which the desired value can be found. During lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored.
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains: data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that access time is linear. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.
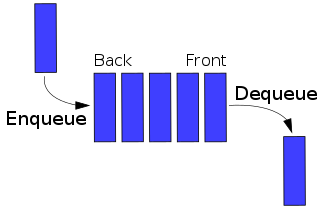
In computer science, a queue is a collection of entities that are maintained in a sequence and can be modified by the addition of entities at one end of the sequence and the removal of entities from the other end of the sequence. By convention, the end of the sequence at which elements are added is called the back, tail, or rear of the queue, and the end at which elements are removed is called the head or front of the queue, analogously to the words used when people line up to wait for goods or services.
A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For random access patterns drawn from a non-uniform random distribution, their amortized time can be faster than logarithmic, proportional to the entropy of the access pattern. For many patterns of non-random operations, also, splay trees can take better than logarithmic time, without requiring advance knowledge of the pattern. According to the unproven dynamic optimality conjecture, their performance on all access patterns is within a constant factor of the best possible performance that could be achieved by any other self-adjusting binary search tree, even one selected to fit that pattern. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.
In computer science, best, worst, and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively. Usually the resource being considered is running time, i.e. time complexity, but could also be memory or some other resource. Best case is the function which performs the minimum number of steps on input data of n elements. Worst case is the function which performs the maximum number of steps on input data of size n. Average case is the function which performs an average number of steps on input data of n elements.

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.
In computer science, amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations in a sequence over that sequence. As a conclusion: "Amortized analysis is a useful tool that complements other techniques such as worst-case and average-case analysis."
In computer science, a Fibonacci heap is a data structure for priority queue operations, consisting of a collection of heap-ordered trees. It has a better amortized running time than many other priority queue data structures including the binary heap and binomial heap. Michael L. Fredman and Robert E. Tarjan developed Fibonacci heaps in 1984 and published them in a scientific journal in 1987. Fibonacci heaps are named after the Fibonacci numbers, which are used in their running time analysis.
In information theory, linguistics, and computer science, the Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two words is the minimum number of single-character edits required to change one word into the other. It is named after the Soviet mathematician Vladimir Levenshtein, who considered this distance in 1965.
In computing, a persistent data structure or not ephemeral data structure is a data structure that always preserves the previous version of itself when it is modified. Such data structures are effectively immutable, as their operations do not (visibly) update the structure in-place, but instead always yield a new updated structure. The term was introduced in Driscoll, Sarnak, Sleator, and Tarjans' 1986 article.
In computer science, a scapegoat tree is a self-balancing binary search tree, invented by Arne Andersson in 1989 and again by Igal Galperin and Ronald L. Rivest in 1993. It provides worst-case lookup time and amortized insertion and deletion time.

In computer science, a dynamic array, growable array, resizable array, dynamic table, mutable array, or array list is a random access, variable-size list data structure that allows elements to be added or removed. It is supplied with standard libraries in many modern mainstream programming languages. Dynamic arrays overcome a limit of static arrays, which have a fixed capacity that needs to be specified at allocation.
In computer science, weight-balanced binary trees (WBTs) are a type of self-balancing binary search trees that can be used to implement dynamic sets, dictionaries (maps) and sequences. These trees were introduced by Nievergelt and Reingold in the 1970s as trees of bounded balance, or BB[α] trees. Their more common name is due to Knuth.
In computational complexity theory, the potential method is a method used to analyze the amortized time and space complexity of a data structure, a measure of its performance over sequences of operations that smooths out the cost of infrequent but expensive operations.
In computer science, dynamic perfect hashing is a programming technique for resolving collisions in a hash table data structure. While more memory-intensive than its hash table counterparts, this technique is useful for situations where fast queries, insertions, and deletions must be made on a large set of elements.

In computer science, a queap is a priority queue data structure. The data structure allows insertions and deletions of arbitrary elements, as well as retrieval of the highest-priority element. Each deletion takes amortized time logarithmic in the number of items that have been in the structure for a longer time than the removed item. Insertions take constant amortized time.
In computing, sequence containers refer to a group of container class templates in the standard library of the C++ programming language that implement storage of data elements. Being templates, they can be used to store arbitrary elements, such as integers or custom classes. One common property of all sequential containers is that the elements can be accessed sequentially. Like all other standard library components, they reside in namespace std.
In computer science, the order-maintenance problem involves maintaining a totally ordered set supporting the following operations:
In computer science, a shadow heap is a mergeable heap data structure which supports efficient heap merging in the amortized sense. More specifically, shadow heaps make use of the shadow merge algorithm to achieve insertion in O(f ) amortized time and deletion in O( /f ) amortized time, for any choice of 1 ≤ f(n) ≤ log log n.







