In probability theory, the central limit theorem (CLT) establishes that, in many situations, for identically distributed independent samples, the standardized sample mean tends towards the standard normal distribution even if the original variables themselves are not normally distributed.
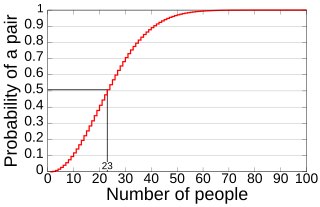
In probability theory, the birthday problem asks for the probability that, in a set of n randomly chosen people, at least two will share a birthday. The birthday paradox refers to the counterintuitive fact that only 23 people are needed for that probability to exceed 50%.

In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli, is the discrete probability distribution of a random variable which takes the value 1 with probability and the value 0 with probability . Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes–no question. Such questions lead to outcomes that are boolean-valued: a single bit whose value is success/yes/true/one with probability p and failure/no/false/zero with probability q. It can be used to represent a coin toss where 1 and 0 would represent "heads" and "tails", respectively, and p would be the probability of the coin landing on heads. In particular, unfair coins would have
In statistics, an effect size is a value measuring the strength of the relationship between two variables in a population, or a sample-based estimate of that quantity. It can refer to the value of a statistic calculated from a sample of data, the value of a parameter for a hypothetical population, or to the equation that operationalizes how statistics or parameters lead to the effect size value. Examples of effect sizes include the correlation between two variables, the regression coefficient in a regression, the mean difference, or the risk of a particular event happening. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses. The cluster of data-analysis methods concerning effect sizes is referred to as estimation statistics.
In statistics, the delta method is a result concerning the approximate probability distribution for a function of an asymptotically normal statistical estimator from knowledge of the limiting variance of that estimator.
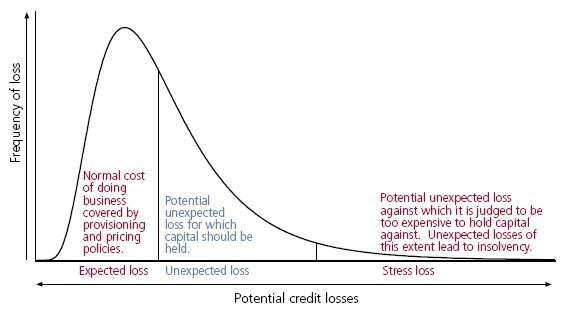
The term Foundation IRB or F-IRB is an abbreviation of foundation internal ratings-based approach, and it refers to a set of credit risk measurement techniques proposed under Basel II capital adequacy rules for banking institutions.
Probability of default (PD) is a financial term describing the likelihood of a default over a particular time horizon. It provides an estimate of the likelihood that a borrower will be unable to meet its debt obligations.
Loss given default or LGD is the share of an asset that is lost if a borrower defaults.
Exposure at default or (EAD) is a parameter used in the calculation of economic capital or regulatory capital under Basel II for a banking institution. It can be defined as the gross exposure under a facility upon default of an obligor.

The risk difference (RD), excess risk, or attributable risk is the difference between the risk of an outcome in the exposed group and the unexposed group. It is computed as , where is the incidence in the exposed group, and is the incidence in the unexposed group. If the risk of an outcome is increased by the exposure, the term absolute risk increase (ARI) is used, and computed as . Equivalently, if the risk of an outcome is decreased by the exposure, the term absolute risk reduction (ARR) is used, and computed as .
In computational complexity theory and quantum computing, Simon's problem is a computational problem that is proven to be solved exponentially faster on a quantum computer than on a classical computer. The quantum algorithm solving Simon's problem, usually called Simon's algorithm, served as the inspiration for Shor's algorithm. Both problems are special cases of the abelian hidden subgroup problem, which is now known to have efficient quantum algorithms.
The Gamow factor, Sommerfeld factor or Gamow–Sommerfeld factor, named after its discoverer George Gamow or after Arnold Sommerfeld, is a probability factor for two nuclear particles' chance of overcoming the Coulomb barrier in order to undergo nuclear reactions, for example in nuclear fusion. By classical physics, there is almost no possibility for protons to fuse by crossing each other's Coulomb barrier at temperatures commonly observed to cause fusion, such as those found in the sun. When George Gamow instead applied quantum mechanics to the problem, he found that there was a significant chance for the fusion due to tunneling.
Expected loss is the sum of the values of all possible losses, each multiplied by the probability of that loss occurring.

The generalized gamma distribution is a continuous probability distribution with two shape parameters. It is a generalization of the gamma distribution which has one shape parameter. Since many distributions commonly used for parametric models in survival analysis are special cases of the generalized gamma, it is sometimes used to determine which parametric model is appropriate for a given set of data. Another example is the half-normal distribution.
Credit valuation adjustments (CVAs) are accounting adjustments made to reserve a portion of profits on uncollateralized financial derivatives. They are charged by a bank to a risky counterparty to compensate the bank for taking on the credit risk of the counterparty during the life of the transaction. These most common transaction types are interest rate derivatives, foreign exchange derivatives, and combinations thereof. The reserved profits can be viewed mathematically as the net present value of the credit risk embedded in the transaction.
Basel III is the third Basel Accord, a framework that sets international standards for bank capital adequacy, stress testing, and liquidity requirements. Augmenting and superseding parts of the Basel II standards, it was developed in response to the deficiencies in financial regulation revealed by the financial crisis of 2007–08. It is intended to strengthen bank capital requirements by increasing minimum capital requirements, holdings of high quality liquid assets, and decreasing bank leverage.
Under the Basel II guidelines, banks are allowed to use their own estimated risk parameters for the purpose of calculating regulatory capital. This is known as the internal ratings-based (IRB) approach to capital requirements for credit risk. Only banks meeting certain minimum conditions, disclosure requirements and approval from their national supervisor are allowed to use this approach in estimating capital for various exposures.
The Basel III: Finalising post-crisis reform standards, sometimes called Basel 3.1 or Basel IV, are changes to international standards for bank capital requirements that were agreed by the Basel Committee on Banking Supervision (BCBS) in 2017 and are due for implementation in January 2023. They amend the international banking standards known as the Basel Accords.
The credit conversion factor (CCF) is a coefficient in the field of credit rating. It is the ratio between the additional amount of a loan used in the future and the amount that could be claimed.
The standardized approach for counterparty credit risk (SA-CCR) is the capital requirement framework under Basel III addressing counterparty risk for derivative trades. It was published by the Basel Committee in March 2014.