
In mathematics, an associative algebra is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.

In mathematics convolution is a mathematical operation on two functions that produces a third function expressing how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reversed and shifted.

In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams 1948. The interaction of subatomic particles can be complex and difficult to understand. Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries. They are

In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold, that measures the extent to which the metric tensor is not locally isometric to that of Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection.
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ. The Laplacian ∇·∇f(p) of a function f at a point p is the rate at which the average value of f over spheres centered at p deviates from f(p) as the radius of the sphere shrinks towards 0. In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form.
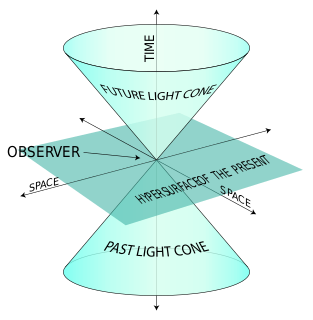
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant four-momentum of a particle with relativistic energy E and three-momentum p = = γmv, where v is the particle's three-velocity and γ the Lorentz factor, is

In special relativity, a four-vector is an object with four components, which transform in a specific way under Lorentz transformation. Specifically, a four-vector is an element of a four-dimensional vector space considered as a representation space of the standard representation of the Lorentz group, the (½,½) representation. It differs from a Euclidean vector in how its magnitude is determined. The transformations that preserve this magnitude are the Lorentz transformations, which include spatial rotations and boosts.
In mathematics, Hodge theory, named after W. V. D. Hodge, is a method for studying the cohomology groups of a smooth manifold M using partial differential equations. The key observation is that, given a Riemannian metric on M, every cohomology class has a canonical representative, a differential form which vanishes under the Laplacian operator of the metric. Such forms are called harmonic.

In mathematics, a vertex operator algebra (VOA) is an algebraic structure that plays an important role in two-dimensional conformal field theory and string theory. In addition to physical applications, vertex operator algebras have proven useful in purely mathematical contexts such as monstrous moonshine and the geometric Langlands correspondence.
Linear time-invariant theory, commonly known as LTI system theory, investigates the response of a linear and time-invariant system to an arbitrary input signal. Trajectories of these systems are commonly measured and tracked as they move through time, but in applications like image processing and field theory, the LTI systems also have trajectories in spatial dimensions. Thus, these systems are also called linear translation-invariant to give the theory the most general reach. In the case of generic discrete-time systems, linear shift-invariant is the corresponding term. A good example of LTI systems are electrical circuits that can be made up of resistors, capacitors, and inductors.. It has been used in applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas.
In mathematics, a symplectic integrator (SI) is a numerical integration scheme for Hamiltonian systems. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations. They are widely used in nonlinear dynamics, molecular dynamics, discrete element methods, accelerator physics, plasma physics, quantum physics, and celestial mechanics.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.
In mathematics — specifically, in stochastic analysis — an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô.
In mathematics, some boundary value problems can be solved using the methods of stochastic analysis. Perhaps the most celebrated example is Shizuo Kakutani's 1944 solution of the Dirichlet problem for the Laplace operator using Brownian motion. However, it turns out that for a large class of semi-elliptic second-order partial differential equations the associated Dirichlet boundary value problem can be solved using an Itō process that solves an associated stochastic differential equation.
In mathematics, a matrix function is a function which maps a matrix to another matrix.
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G. The key examples are the matrix coefficients of the spherical principal series, the irreducible representations appearing in the decomposition of the unitary representation of G on L2(G/K). In this case the commutant of G is generated by the algebra of biinvariant functions on G with respect to K acting by right convolution. It is commutative if in addition G/K is a symmetric space, for example when G is a connected semisimple Lie group with finite centre and K is a maximal compact subgroup. The matrix coefficients of the spherical principal series describe precisely the spectrum of the corresponding C* algebra generated by the biinvariant functions of compact support, often called a Hecke algebra. The spectrum of the commutative Banach *-algebra of biinvariant L1 functions is larger; when G is a semisimple Lie group with maximal compact subgroup K, additional characters come from matrix coefficients of the complementary series, obtained by analytic continuation of the spherical principal series.
In mathematics, Capelli's identity, named after Alfredo Capelli (1887), is an analogue of the formula det(AB) = det(A) det(B), for certain matrices with noncommuting entries, related to the representation theory of the Lie algebra . It can be used to relate an invariant ƒ to the invariant Ωƒ, where Ω is Cayley's Ω process.

In the theory of Lie groups, Lie algebras and their representation theory, a Lie algebra extensione is an enlargement of a given Lie algebra g by another Lie algebra h. Extensions arise in several ways. There is the trivial extension obtained by taking a direct sum of two Lie algebras. Other types are the split extension and the central extension. Extensions may arise naturally, for instance, when forming a Lie algebra from projective group representations. Such a Lie algebra will contain central charges.
In mathematics, the Fuglede−Kadison determinant of an invertible operator in a finite factor is a positive real number associated with it. It defines a multiplicative homomorphism from the set of invertible operators to the set of positive real numbers. The Fuglede−Kadison determinant of an operator is often denoted by .
















































