In geography, latitude is a geographic coordinate that specifies the north–south position of a point on the Earth's surface. Latitude is an angle which ranges from 0° at the Equator to 90° at the poles. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude is used together with longitude to specify the precise location of features on the surface of the Earth. On its own, the term latitude should be taken to be the geodetic latitude as defined below. Briefly, geodetic latitude at a point is the angle formed by the vector perpendicular to the ellipsoidal surface from that point, and the equatorial plane. Also defined are six auxiliary latitudes which are used in special applications.
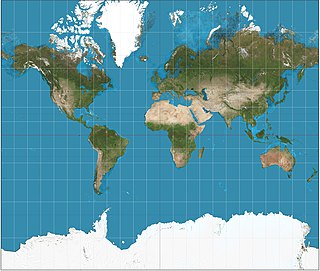
The Mercator projection is a cylindrical map projection presented by the Flemish geographer and cartographer Gerardus Mercator in 1569. It became the standard map projection for nautical navigation because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as straight segments that conserve the angles with the meridians. Although the linear scale is equal in all directions around any point, thus preserving the angles and the shapes of small objects, the Mercator projection distorts the size of objects as the latitude increases from the Equator to the poles, where the scale becomes infinite. So, for example, landmasses such as Greenland and Antarctica appear much larger than they actually are, relative to landmasses near the equator such as Central Africa.
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation. An elliptically polarized wave may be resolved into two linearly polarized waves in phase quadrature, with their polarization planes at right angles to each other. Since the electric field can rotate clockwise or counterclockwise as it propagates, elliptically polarized waves exhibit chirality.
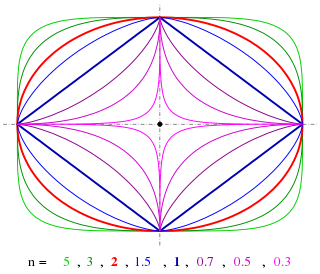
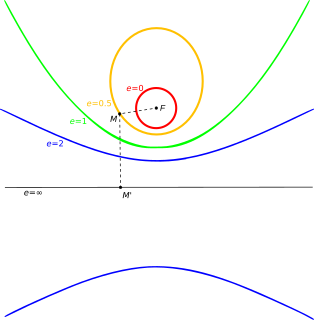
A superellipse, also known as a Lamé curve after Gabriel Lamé, is a closed curve resembling the ellipse, retaining the geometric features of semi-major axis and semi-minor axis, and symmetry about them, but a different overall shape.

Angular displacement of a body is the angle in radians through which a point revolves around a centre or line has been rotated in a specified sense about a specified axis. When a body rotates about its axis, the motion cannot simply be analyzed as a particle, as in circular motion it undergoes a changing velocity and acceleration at any time (t). When dealing with the rotation of a body, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the body's motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is minimal and negligible. Thus the rotation of a rigid body over a fixed axis is referred to as rotational motion.
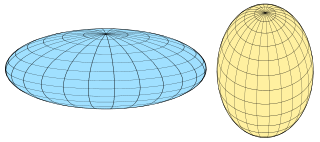
A spheroid, or ellipsoid of revolution, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.

In geodesy, a reference ellipsoid is a mathematically defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body. Because of their relative simplicity, reference ellipsoids are used as a preferred surface on which geodetic network computations are performed and point coordinates such as latitude, longitude, and elevation are defined.
In orbital mechanics, eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit. The eccentric anomaly is one of three angular parameters ("anomalies") that define a position along an orbit, the other two being the true anomaly and the mean anomaly.
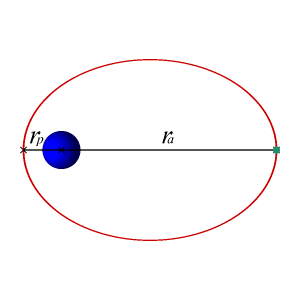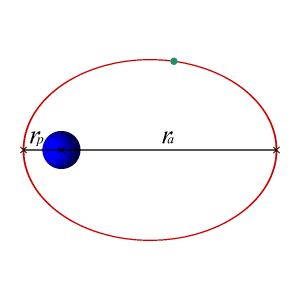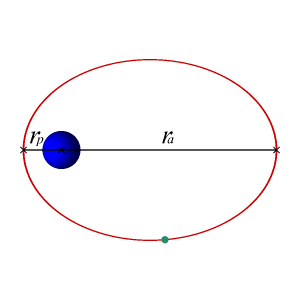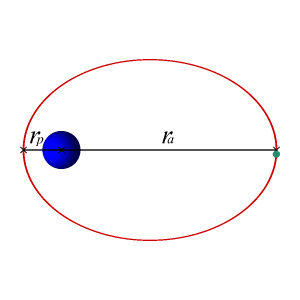
In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1. In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1.
Spacecraft flight dynamics is the science of space vehicle performance, stability, and control. It requires analysis of the six degrees of freedom of the vehicle's flight, which are similar to those of aircraft: translation in three dimensional axes; and its orientation about the vehicle's center of mass in these axes, known as pitch, roll and yaw, with respect to a defined frame of reference.
The scale of a map is the ratio of a distance on the map to the corresponding distance on the ground. This simple concept is complicated by the curvature of the Earth's surface, which forces scale to vary across a map. Because of this variation, the concept of scale becomes meaningful in two distinct ways. The first way is the ratio of the size of the generating globe to the size of the Earth. The generating globe is a conceptual model to which the Earth is shrunk and from which the map is projected.
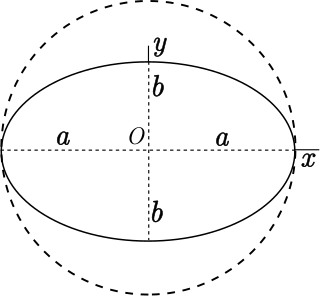
Flattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The usual notation for flattening is f and its definition in terms of the semi-axes of the resulting ellipse or ellipsoid is

In cartography, a Tissot's indicatrix is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 and 1871 in order to characterize local distortions due to map projection. It is the geometry that results from projecting a circle of infinitesimal radius from a curved geometric model, such as a globe, onto a map. Tissot proved that the resulting diagram is an ellipse whose axes indicate the two principal directions along which scale is maximal and minimal at that point on the map.

The Aitoff projection is a modified azimuthal map projection proposed by David A. Aitoff in 1889. Based on the equatorial form of the azimuthal equidistant projection, Aitoff first halves longitudes, then projects according to the azimuthal equidistant, and then stretches the result horizontally into a 2:1 ellipse to compensate for having halved the longitudes. Expressed simply:

A great ellipse is an ellipse passing through two points on a spheroid and having the same center as that of the spheroid. Equivalently, it is an ellipse on the surface of a spheroid and centered on the origin, or the curve formed by intersecting the spheroid by a plane through its center. For points that are separated by less than about a quarter of the circumference of the earth, about , the length of the great ellipse connecting the points is close to the geodesic distance.
In geodesy, a meridian arc measurement is the distance between two points with the same longitude, i.e., a segment of a meridian curve or its length. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This process is called the determination of the figure of the Earth. The earliest determinations of the size of a spherical Earth required a single arc. The latest determinations use astro-geodetic measurements and the methods of satellite geodesy to determine the reference ellipsoids.
Vincenty's formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty (1975a). They are based on the assumption that the figure of the Earth is an oblate spheroid, and hence are more accurate than methods that assume a spherical Earth, such as great-circle distance.

In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the widest points of the perimeter. The semi-major axis is one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. For the special case of a circle, the semi-major axis is the radius.

The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an oblate ellipsoid, a slightly flattened sphere. A geodesic is the shortest path between two points on a curved surface, i.e., the analogue of a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry.