Areal velocity

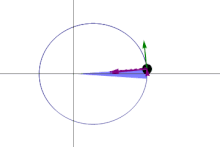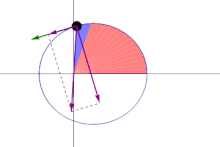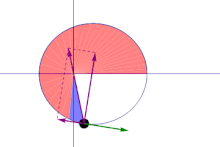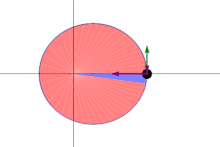
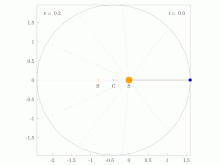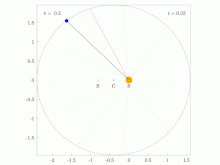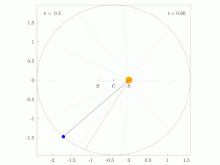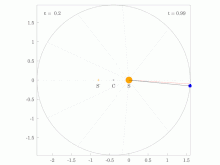
Areal velocity is the area swept out per unit time by the position vector of a particle moving along a curve da/dt=const (shown in blue).

In classical mechanics, areal velocity (also called sector velocity or sectorial velocity) is a pseudovector whose length equals the rate of change at which area is swept out by a particle as it moves along a curve.^{[ clarification needed ]}

In the adjoining figure, suppose that a particle moves along the blue curve. At a certain time t, the particle is located at point B, and a short while later, at time t + Δt, the particle has moved to point C. The region swept out by the particle is shaded in green in the figure, bounded by the line segments AB and AC and the curve along which the particle moves. The areal velocity magnitude (i.e., the areal speed ) is this region's area divided by the time interval Δt in the limit that Δt becomes vanishingly small. The vector direction is postulated to be normal to the plane containing the position and velocity vectors of the particle, following a convention known as the right hand rule.

Illustration of Kepler's second law. The planet moves faster near the Sun, so the same area is swept out in a given time as at larger distances, where the planet moves more slowly.

Areal velocity is closely related to angular momentum. Any object has an orbital angular momentum about an origin, and this turns out to be, up to a multiplicative scalar constant, equal to the areal velocity of the object about the same origin. A crucial property of angular momentum is that it is conserved under the action of central forces (i.e. forces acting radially toward or away from the origin). Historically, the law of conservation of angular momentum was stated entirely in terms of areal velocity. A special case of this is Kepler's second law, which states that the areal velocity of a planet, with the sun taken as origin, is constant with time. Because the gravitational force acting on a planet is approximately a central force (since the mass of the planet is small in comparison to that of the sun), the angular momentum of the planet (and hence the areal velocity) must remain (approximately) constant. Isaac Newton was the first scientist to recognize the dynamical significance of Kepler's second law. With the aid of his laws of motion, he proved in 1684 that any planet that is attracted to a fixed center sweeps out equal areas in equal intervals of time. For this reason, the law of conservation of angular momentum was historically called the "principle of equal areas". The law of conservation of angular momentum was later expanded and generalized to more complicated situations not easily describable via the concept of areal velocity. Since the modern form of the law of conservation of angular momentum includes much more than just Kepler's second law, the designation "principle of equal areas" has been dropped in modern works.

Orbits of planets with varying eccentricities. The red ray rotates at a constant angular velocity and with the same orbital time period as the planet, ${\displaystyle T=1}$.

S: Sun at the primary focus, C: Centre of ellipse, S': The secondary focus.

In each case, the area of all sectors depicted is identical.

Low	High
Planet orbiting the Sun in a circular orbit (e=0.0)	Planet orbiting the Sun in an orbit with e=0.5
Planet orbiting the Sun in an orbit with e=0.2	Planet orbiting the Sun in an orbit with e=0.8

Areal velocity is also closely related to the concept of magnetic dipoles in classical electrodynamics. Every electric current possesses a (pseudo)vectorial quantity called a magnetic dipole moment about a given origin. In the special case that the current consists of a single moving point charge, the magnetic dipole moment about any given origin turns out to be, up to a scalar factor, equal to the areal velocity of the charge about the same origin. In the more general case where the current consists of a large but finite number of moving point charges, the magnetic dipole moment is the sum of the dipole moments of each of the charges, and hence, is proportional to the sum of the areal velocities of all the charges. In the continuity limit where the number of charges in the current becomes infinite, the sum becomes an integral; i.e., the magnetic dipole moment of a continuous current about a given origin is, up to a scalar factor, equal to the integral of the areal velocity along the current path. If the current path happens to be a closed loop and if the current is the same at all points in the loop, this integral turns out to be independent of the chosen origin, so that the magnetic dipole moment becomes a fundamental constant associated with the current loop.

Connection with angular momentum

In the situation of the first figure, the area swept out during time period Δt by the particle is approximately equal to the area of triangle ABC. As Δt approaches zero this near-equality becomes exact as a limit.

Let the point D be the fourth corner of parallelogram ABDC shown in the figure, so that the vectors AB and AC add up by the parallelogram rule to vector AD. Then the area of triangle ABC is half the area of parallelogram ABDC, and the area of ABDC is equal to the magnitude of the cross product of vectors AB and AC. This area can also be viewed as a (pseudo)vector with this magnitude, and pointing in a direction perpendicular to the parallelogram (following the right hand rule); this vector is the cross product itself:

$${\displaystyle {\text{vector area of parallelogram }}ABCD=\mathbf {r} (t)\times \mathbf {r} (t+\Delta t).}$$

Hence

$${\displaystyle {\text{vector area of triangle }}ABC={\frac {\mathbf {r} (t)\times \mathbf {r} (t+\Delta t)}{2}}.}$$

The areal velocity is this vector area divided by Δt in the limit that Δt becomes vanishingly small:

$${\displaystyle {\begin{aligned}{\text{areal velocity}}&=\lim _{\Delta t\rightarrow 0}{\frac {\mathbf {r} (t)\times \mathbf {r} (t+\Delta t)}{2\Delta t}}\\&=\lim _{\Delta t\rightarrow 0}{\frac {\mathbf {r} (t)\times {\bigl (}\mathbf {r} (t)+\mathbf {r} \,'(t)\Delta t{\bigr )}}{2\Delta t}}\\&=\lim _{\Delta t\rightarrow 0}{\frac {\mathbf {r} (t)\times \mathbf {r} \,'(t)}{2}}\left({\Delta t \over \Delta t}\right)\\&={\frac {\mathbf {r} (t)\times \mathbf {r} \,'(t)}{2}}.\end{aligned}}}$$

But, ${\displaystyle \mathbf {r} \,'(t)}$ is the velocity vector ${\displaystyle \mathbf {v} (t)}$ of the moving particle, so that

$${\displaystyle {\frac {d\mathbf {A} }{dt}}={\frac {\mathbf {r} \times \mathbf {v} }{2}}.}$$

On the other hand, the angular momentum of the particle is

$${\displaystyle \mathbf {L} =\mathbf {r} \times m\mathbf {v} ,}$$

and hence the angular momentum equals 2m times the areal velocity.

Conservation of areal velocity is a general property of central force motion, ^[1] and, within the context of classical mechanics, is equivalent to the conservation of angular momentum.

See also

• Angular momentum
• Specific angular momentum
• Elliptic coordinate system

References

1. Houde, Martin (November 10, 2005). "Chapter 6. Central Force Motion" (PDF). Physics 350/Applied Math 353 Classical Mechanics I. Western University. Retrieved October 15, 2021.

Further reading

• Moulton, F. R. (1970) [1914]. An Introduction to Celestial Mechanics. Dover. ISBN   978-0-486-64687-9.
• Goldstein, H. (1980). Classical Mechanics (2nd ed.). Addison-Wesley. ISBN   978-0-486-68063-7.
• Casey, J. (2007). "Areal Velocity and Angular Momentum for Non-Planar Problems in Particle Mechanics". American Journal of Physics. 75 (8): 677–685. Bibcode:2007AmJPh..75..677C. doi: 10.1119/1.2735630 .
• Brackenridge, J. B. (1995). The Key to Newton's Dynamics: The Kepler Problem and the Principia . Berkeley: University of California Press. ISBN   978-0-520-20217-7. JSTOR   10.1525/j.ctt1ppn2m.