
In mathematics, the absolute value or modulus of a real number , denoted , is the non-negative value of without regard to its sign. Namely, if is a positive number, and if is negative, and . For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its distance from zero.
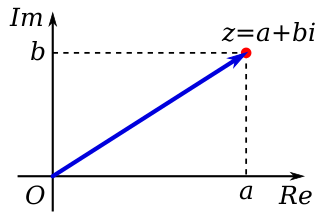
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation ; every complex number can be expressed in the form , where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number , a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.

In geometry, a Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, called coordinate lines, coordinate axes or just axes of the system. The point where they meet is called the origin and has (0, 0) as coordinates.
In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod p when p is a prime number.
An imaginary number is a real number multiplied by the imaginary unit i, which is defined by its property i2 = −1. The square of an imaginary number bi is −b2. For example, 5i is an imaginary number, and its square is −25. By definition, zero is considered to be both real and imaginary.
In probability theory and statistics, a central moment is a moment of a probability distribution of a random variable about the random variable's mean; that is, it is the expected value of a specified integer power of the deviation of the random variable from the mean. The various moments form one set of values by which the properties of a probability distribution can be usefully characterized. Central moments are used in preference to ordinary moments, computed in terms of deviations from the mean instead of from zero, because the higher-order central moments relate only to the spread and shape of the distribution, rather than also to its location.

In mathematics, Euler's identity is the equality

The imaginary unit or unit imaginary number is a solution to the quadratic equation . Although there is no real number with this property, i can be used to extend the real numbers to what are called complex numbers, using addition and multiplication. A simple example of the use of i in a complex number is .

In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the x-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and vice versa; this is the basis of analytic geometry.

In mathematics, exponentiation is an operation involving two numbers, the base and the exponent or power. Exponentiation is written as bn, where b is the base and n is the power; this is pronounced as "b (raised) to the n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.

In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the x-axis, called the real axis, is formed by the real numbers, and the y-axis, called the imaginary axis, is formed by the imaginary numbers.

In mathematics, a multivalued function is a set-valued function with additional properties depending on context. The terms multifunction and many-valued function are sometimes also used.
In mathematics, taking the nth root is an operation involving two numbers, the radicand and the index or degree. Taking the nth root is written as , where x is the radicand and n is the index. This is pronounced as "the nth root of x". The definition then of an nth root of a number x is a number r which, when raised to the power of the positive integer n, yields x:

In mathematics, especially in the group theoretic area of algebra, the projective linear group (also known as the projective general linear group or PGL) is the induced action of the general linear group of a vector space V on the associated projective space P(V). Explicitly, the projective linear group is the quotient group

In mathematics, tetration is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though and the left-exponent xb are common.
Jean-Robert Argand was a Genevan amateur mathematician. In 1806, while managing a bookstore in Paris, he published the idea of geometrical interpretation of complex numbers known as the Argand diagram and is known for the first rigorous proof of the Fundamental Theorem of Algebra.

In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted E2. It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement.
Mathematical diagrams, such as charts and graphs, are mainly designed to convey mathematical relationships—for example, comparisons over time.
In mathematics and more specifically in field theory, a radical extension of a field K is an extension of K that is obtained by adjoining a sequence of nth roots of elements.












