In mathematics, a directed set is a nonempty set together with a reflexive and transitive binary relation , with the additional property that every pair of elements has an upper bound. In other words, for any and in there must exist in with and A directed set's preorder is called a direction.

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order."
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum (join) and an infimum (meet). A lattice which satisfies at least one of these properties is known as a conditionally complete lattice. Specifically, every non-empty finite lattice is complete. Complete lattices appear in many applications in mathematics and computer science. Being a special instance of lattices, they are studied both in order theory and universal algebra.

In mathematical analysis and related areas of mathematics, a set is called bounded if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded. The word 'bounded' makes no sense in a general topological space without a corresponding metric.

Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory. It states that a partially ordered set containing upper bounds for every chain necessarily contains at least one maximal element.

In mathematics, especially in order theory, a maximal element of a subset S of some preordered set is an element of S that is not smaller than any other element in S. A minimal element of a subset S of some preordered set is defined dually as an element of S that is not greater than any other element in S.
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.
This is a glossary of some terms used in various branches of mathematics that are related to the fields of order, lattice, and domain theory. Note that there is a structured list of order topics available as well. Other helpful resources might be the following overview articles:
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.
In mathematics, the phrase complete partial order is variously used to refer to at least three similar, but distinct, classes of partially ordered sets, characterized by particular completeness properties. Complete partial orders play a central role in theoretical computer science: in denotational semantics and domain theory.

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included. Antimatroids are commonly axiomatized in two equivalent ways, either as a set system modeling the possible states of such a process, or as a formal language modeling the different sequences in which elements may be included. Dilworth (1940) was the first to study antimatroids, using yet another axiomatization based on lattice theory, and they have been frequently rediscovered in other contexts.
In the mathematical area of order theory, the compact elements or finite elements of a partially ordered set are those elements that cannot be subsumed by a supremum of any non-empty directed set that does not already contain members above the compact element. This notion of compactness simultaneously generalizes the notions of finite sets in set theory, compact sets in topology, and finitely generated modules in algebra.
In set theory, a tree is a partially ordered set (T, <) such that for each t ∈ T, the set {s ∈ T : s < t} is well-ordered by the relation <. Frequently trees are assumed to have only one root, as the typical questions investigated in this field are easily reduced to questions about single-rooted trees.
In the mathematical field of order theory, a partially ordered set is bounded complete if all of its subsets that have some upper bound also have a least upper bound. Such a partial order can also be called consistently or coherently complete, since any upper bound of a set can be interpreted as some consistent (non-contradictory) piece of information that extends all the information present in the set. Hence the presence of some upper bound in a way guarantees the consistency of a set. Bounded completeness then yields the existence of a least upper bound of any "consistent" subset, which can be regarded as the most general piece of information that captures all the knowledge present within this subset. This view closely relates to the idea of information ordering that one typically finds in domain theory.
In the mathematical fields of order and domain theory, a Scott domain is an algebraic, bounded-complete cpo. They are named in honour of Dana S. Scott, who was the first to study these structures at the advent of domain theory. Scott domains are very closely related to algebraic lattices, being different only in possibly lacking a greatest element. They are also closely related to Scott information systems, which constitute a "syntactic" representation of Scott domains.
In mathematics, a join-semilattice is a partially ordered set that has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset. Every join-semilattice is a meet-semilattice in the inverse order and vice versa.
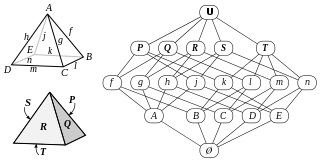
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines.

In mathematics, in the branch of combinatorics, a graded poset is a partially-ordered set (poset) P equipped with a rank functionρ from P to the set N of all natural numbers. ρ must satisfy the following two properties:

In the branch of mathematics known as order theory, a semimodular lattice, is a lattice that satisfies the following condition:
In the mathematics of matroids and lattices, a geometric lattice is a finite atomistic semimodular lattice, and a matroid lattice is an atomistic semimodular lattice without the assumption of finiteness. Geometric lattices and matroid lattices, respectively, form the lattices of flats of finite and infinite matroids, and every geometric or matroid lattice comes from a matroid in this way.








