Related Research Articles

In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra.
In mathematics, a total order or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation on some set , which satisfies the following for all and in :
- (reflexive).
- If and then (transitive).
- If and then (antisymmetric).
- or .
In algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.
In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism—given as such a lattice of sets.
In mathematics, the Boolean prime ideal theorem states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on sets is known as the ultrafilter lemma. Other theorems are obtained by considering different mathematical structures with appropriate notions of ideals, for example, rings and prime ideals, or distributive lattices and maximal ideals. This article focuses on prime ideal theorems from order theory.
In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation theorem for Boolean algebras. These concepts are named in honor of Marshall Stone. Stone-type dualities also provide the foundation for pointless topology and are exploited in theoretical computer science for the study of formal semantics.
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.
In mathematics, a closure operator on a set S is a function from the power set of S to itself that satisfies the following conditions for all sets
In mathematical order theory, an ideal is a special subset of a partially ordered set (poset). Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion. Ideals are of great importance for many constructions in order and lattice theory.
In mathematics, a spectral space is a topological space that is homeomorphic to the spectrum of a commutative ring. It is sometimes also called a coherent space because of the connection to coherent topoi.

Richard Melvin Schoen is an American mathematician known for his work in differential geometry and geometric analysis. He is best known for the resolution of the Yamabe problem in 1984.
In mathematics, many types of algebraic structures are studied. Abstract algebra is primarily the study of specific algebraic structures and their properties. Algebraic structures may be viewed in different ways, however the common starting point of algebra texts is that an algebraic object incorporates one or more sets with one or more binary operations or unary operations satisfying a collection of axioms.
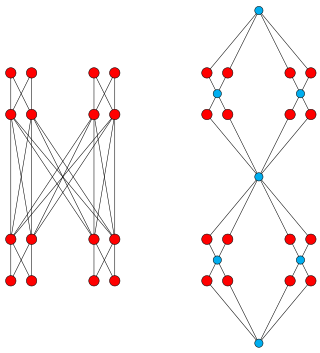
In mathematics, specifically order theory, the Dedekind–MacNeille completion of a partially ordered set is the smallest complete lattice that contains it. It is named after Holbrook Mann MacNeille whose 1937 paper first defined and constructed it, and after Richard Dedekind because its construction generalizes the Dedekind cuts used by Dedekind to construct the real numbers from the rational numbers. It is also called the completion by cuts or normal completion.
In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets. Here, a lattice is an abstract structure with two binary operations, the "meet" and "join" operations, which must obey certain axioms; it is distributive if these two operations obey the distributive law. The union and intersection operations, in a family of sets that is closed under these operations, automatically form a distributive lattice, and Birkhoff's representation theorem states that every finite distributive lattice can be formed in this way. It is named after Garrett Birkhoff, who published a proof of it in 1937.
In mathematics, a Priestley space is an ordered topological space with special properties. Priestley spaces are named after Hilary Priestley who introduced and investigated them. Priestley spaces play a fundamental role in the study of distributive lattices. In particular, there is a duality between the category of Priestley spaces and the category of bounded distributive lattices.
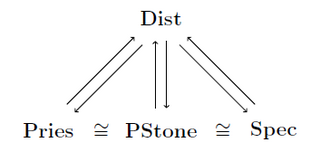
In mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces. This duality, which is originally also due to Marshall H. Stone, generalizes the well-known Stone duality between Stone spaces and Boolean algebras.
In mathematics, in the area of order theory, an upwards centered setS is a subset of a partially ordered set, P, such that any finite subset of S has an upper bound in P. Similarly, any finite subset of a downwards centered set has a lower bound. An upwards centered set can also be called a consistent set. Any directed set is necessarily centered, and any centered set is a linked set.

Wilson Alexander Sutherland was a British mathematician at the University of Oxford.
Introduction to Lattices and Order is a mathematical textbook on order theory by Brian A. Davey and Hilary Priestley. It was published by the Cambridge University Press in their Cambridge Mathematical Textbooks series in 1990, with a second edition in 2002. The second edition is significantly different in its topics and organization, and was revised to incorporate recent developments in the area, especially in its applications to computer science. The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries.
In order theory, a continuous poset is a partially ordered set in which every element is the directed supremum of elements approximating it.
References
- 1 2 Hilary Priestley at the Mathematics Genealogy Project.
- ↑ Gardam, Tim (11 July 2006). "Titles of Distinction awarded to eight Fellows" . Retrieved 11 June 2014.
- ↑ Stralka, Albert (December 1980). "A partially ordered space which is not a priestley space". Semigroup Forum . 20 (1). Springer: 293–297. doi:10.1007/BF02572690. S2CID 123310469.
- ↑ Cignoli, R.; Lafalce, S.; Petrovich, A. (September 1991). "Remarks on Priestley duality for distributive lattices". Order . 8 (3). Springer: 299–315. doi:10.1007/BF00383451. S2CID 122146613.
- ↑ Reviews of Introduction to Lattices and Order: T. S. Blyth, MR 1058437, MR 1902334; Jonathan Cohen, ACM SIGACT News, doi : 10.1145/1233481.1233488; Amy Davidow, Amer. Math. Monthly, JSTOR 2323967; Josef Niederle, Zbl 0701.06001; Václav Slavík, Zbl 1002.06001