Priestley space

Last updated December 10, 2019

In mathematics, a Priestley space is an ordered topological space with special properties. Priestley spaces are named after Hilary Priestley who introduced and investigated them.^[1] Priestley spaces play a fundamental role in the study of distributive lattices. In particular, there is a duality ("Priestley duality"^[2]) between the category of Priestley spaces and the category of bounded distributive lattices.^[3]^[4]

Definition

A Priestley space is an ordered topological space $(X, τ,\leq)$ , i.e. a set $X$ equipped with a partial order $\leq$ and a topology $τ$ , satisfying the following two conditions:

$(X, τ)$ is compact.
If $\scriptstyle x\,\not \leq \,y$ , then there exists a clopen up-set $U$ of $X$ such that $x \in U$ and $y \notin U$ . (This condition is known as the Priestley separation axiom.)

Properties of Priestley spaces

Each Priestley space is Hausdorff. Indeed, given two points $x, y$ of a Priestley space $(X, τ,\leq)$ , if $x \neq y$ , then as $\leq$ is a partial order, either $\scriptstyle x\,\not \leq \,y$ or $\scriptstyle y\,\not \leq \,x$ . Assuming, without loss of generality, that $\scriptstyle x\,\not \leq \,y$ , (ii) provides a clopen up-set $U$ of $X$ such that $x \in U$ and $y \notin U$ . Therefore, $U$ and $V = X - U$ are disjoint open subsets of $X$ separating $x$ and $y$ .
Each Priestley space is also zero-dimensional; that is, each open neighborhood $U$ of a point $x$ of a Priestley space $(X, τ,\leq)$ contains a clopen neighborhood $C$ of $x$ . To see this, one proceeds as follows. For each $y \in X - U$ , either $\scriptstyle x\,\not \leq \,y$ or $\scriptstyle y\,\not \leq \,x$ . By the Priestley separation axiom, there exists a clopen up-set or a clopen down-set containing $x$ and missing $y$ . The intersection of these clopen neighborhoods of $x$ does not meet $X - U$ . Therefore, as $X$ is compact, there exists a finite intersection of these clopen neighborhoods of $x$ missing $X - U$ . This finite intersection is the desired clopen neighborhood $C$ of $x$ contained in $U$ .

It follows that for each Priestley space $(X, τ,\leq)$ , the topological space $(X, τ)$ is a Stone space; that is, it is a compact Hausdorff zero-dimensional space.

Some further useful properties of Priestley spaces are listed below.

Let $(X, τ,\leq)$ be a Priestley space.

(a) For each closed subset

F

of

X

, both

↑ F = {x \in X : y \leq x for some y \in F}

and

↓ F = {x \in X : x \leq y for some y \in F}

are closed subsets of

X

.

(b) Each open up-set of

X

is a union of clopen up-sets of

X

and each open down-set of

X

is a union of clopen down-sets of

X

.

(c) Each closed up-set of

X

is an intersection of clopen up-sets of

X

and each closed down-set of

X

is an intersection of clopen down-sets of

X

.

(d) Clopen up-sets and clopen down-sets of

X

form a subbasis for

(X, τ)

.

(e) For each pair of closed subsets

F

and

G

of

X

, if

↑ F \cap ↓ G = \emptyset

, then there exists a clopen up-set

U

such that

F \subseteq U

and

U \cap G = \emptyset

.

A Priestley morphism from a Priestley space $(X, τ,\leq)$ to another Priestley space $(X', τ',\leq')$ is a map $f : X \to X'$ which is continuous and order-preserving.

Let Pries denote the category of Priestley spaces and Priestley morphisms.

Connection with spectral spaces

Priestley spaces are closely related to spectral spaces. For a Priestley space $(X, τ,\leq)$ , let $τ u$ denote the collection of all open up-sets of $X$ . Similarly, let $τ d$ denote the collection of all open down-sets of $X$ .

Theorem:^[5] If $(X, τ,\leq)$ is a Priestley space, then both $(X, τ u)$ and $(X, τ d)$ are spectral spaces.

Conversely, given a spectral space $(X, τ)$ , let $τ #$ denote the patch topology on $X$ ; that is, the topology generated by the subbasis consisting of compact open subsets of $(X, τ)$ and their complements. Let also $\leq$ denote the specialization order of $(X, τ)$ .

Theorem:^[6] If $(X, τ)$ is a spectral space, then $(X, τ #,\leq)$ is a Priestley space.

In fact, this correspondence between Priestley spaces and spectral spaces is functorial and yields an isomorphism between Pries and the category Spec of spectral spaces and spectral maps.

Connection with bitopological spaces

Priestley spaces are also closely related to bitopological spaces.

Theorem:^[7] If $(X, τ,\leq)$ is a Priestley space, then $(X, τ u, τ d)$ is a pairwise Stone space. Conversely, if $(X, τ 1, τ 2)$ is a pairwise Stone space, then $(X, τ,\leq)$ is a Priestley space, where $τ$ is the join of $τ 1$ and $τ 2$ and $\leq$ is the specialization order of $(X, τ 1)$ .

The correspondence between Priestley spaces and pairwise Stone spaces is functorial and yields an isomorphism between the category Pries of Priestley spaces and Priestley morphisms and the category PStone of pairwise Stone spaces and bi-continuous maps.

Thus, one has the following isomorphisms of categories:

$\mathbf {Spec} \cong \mathbf {Pries} \cong \mathbf {PStone}$

One of the main consequences of the duality theory for distributive lattices is that each of these categories is dually equivalent to the category of bounded distributive lattices.

Notes

↑ Priestley, (1970).
↑ Cignoli, R.; Lafalce, S.; Petrovich, A. (September 1991). "Remarks on Priestley duality for distributive lattices". Order . 8 (3): 299–315. doi:10.1007/BF00383451.
↑ Cornish, (1975).
↑ Bezhanishvili et al. (2010)
↑ Cornish, (1975). Bezhanishvili et al. (2010).
↑ Cornish, (1975). Bezhanishvili et al. (2010).
↑ Bezhanishvili et al. (2010).

Related Research Articles

In mathematics, pointless topology is an approach to topology that avoids mentioning points.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology. Another name for general topology is point-set topology.

In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism—given as such a lattice of sets.

In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation theorem for Boolean algebras. These concepts are named in honor of Marshall Stone. Stone-type dualities also provide the foundation for pointless topology and are exploited in theoretical computer science for the study of formal semantics.

In topology, an Alexandrov topology is a topology in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open; in Alexandrov topologies the finite restriction is dropped.

In mathematics, a spectral space is a topological space that is homeomorphic to the spectrum of a commutative ring.

In mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a certain field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Marshall H. Stone (1936). Stone was led to it by his study of the spectral theory of operators on a Hilbert space.

In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra that is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames. Although these three categories contain the same objects, they differ in their morphisms, and thus get distinct names. Only the morphisms of CHey are homomorphisms of complete Heyting algebras.

In mathematics, a join-semilattice is a partially ordered set that has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset. Every join-semilattice is a meet-semilattice in the inverse order and vice versa.

In mathematics a field of sets is a pair $where is a set and is an algebra over i.e., a non-empty subset of the power set of closed under the intersection and union of pairs of sets and under complements of individual sets. In other words, forms a subalgebra of the power set Boolean algebra of . Elements of are called points and those of are called complexes and are said to be the admissible sets of .$

In general topology and related areas of mathematics, the final topology on a set $, with respect to a family of functions into, is the finest topology on that makes those functions continuous.$

Upper set a subset of a partial order that includes all successors of its elements

In mathematics, an upper set of a partially ordered set is a subset U of X such that if x is in U and x ≤ y, then y is in U. That is, U satisfies the property

In mathematics, a bitopological space is a set endowed with two topologies. Typically, if the set is $and the topologies are and then the bitopological space is referred to as . The notion was introduced by Kelly in the study of quasimetrics, i.e. distance functions that are not required to be symmetric.$

In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets. The theorem can be interpreted as providing a one-to-one correspondence between distributive lattices and partial orders, between quasi-ordinal knowledge spaces and preorders, or between finite topological spaces and preorders. It is named after Garrett Birkhoff, who published a proof of it in 1937.

In mathematics and particularly in topology, pairwise Stone space is a bitopological space $which is pairwise compact, pairwise Hausdorff, and pairwise zero-dimensional.$

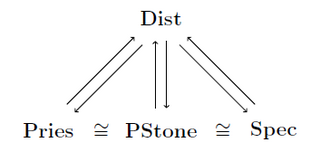
In mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces. This duality, which is originally also due to Marshall H. Stone, generalizes the well-known Stone duality between Stone spaces and Boolean algebras.

In mathematics, Esakia spaces are special ordered topological spaces introduced and studied by Leo Esakia in 1974. Esakia spaces play a fundamental role in the study of Heyting algebras, primarily by virtue of the Esakia duality—the dual equivalence between the category of Heyting algebras and the category of Esakia spaces.

In mathematics, Esakia duality is the dual equivalence between the category of Heyting algebras and the category of Esakia spaces. Esakia duality provides an order-topological representation of Heyting algebras via Esakia spaces.

In mathematics, a linear map is a mapping $V \to W$ between two modules that preserves the operations of addition and scalar multiplication.

In mathematics, a polyadic space is a topological space that is the image under a continuous function of a topological power of an Alexandroff one-point compactification of a discrete topological space.

References

Priestley, H. A. (1970). "Representation of distributive lattices by means of ordered Stone spaces". Bull. London Math. Soc. 2 (2): 186–190. doi:10.1112/blms/2.2.186.
Priestley, H. A. (1972). "Ordered topological spaces and the representation of distributive lattices" (PDF). Proc. London Math. Soc. 24 (3): 507–530. doi:10.1112/plms/s3-24.3.507.
Cornish, W. H. (1975). "On H. Priestley's dual of the category of bounded distributive lattices". Mat. Vesnik. 12 (27): 329–332.
Hochster, M. (1969). "Prime ideal structure in commutative rings". Trans. Amer. Math. Soc. 142: 43–60. doi: 10.1090/S0002-9947-1969-0251026-X .
Bezhanishvili, G.; Bezhanishvili, N.; Gabelaia, D.; Kurz, A (2010). "Bitopological duality for distributive lattices and Heyting algebras" (PDF). Mathematical Structures in Computer Science. 20.
Dickmann, Max; Schwartz, Niels; Tressl, Marcus (2019). Spectral Spaces. New Mathematical Monographs. 35. Cambridge: Cambridge University Press. doi:10.1017/9781316543870. ISBN 978-1-107-14672-3.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Priestley, (1970).

[2] Cignoli, R.; Lafalce, S.; Petrovich, A. (September 1991). "Remarks on Priestley duality for distributive lattices". Order . 8 (3): 299–315. doi:10.1007/BF00383451.

[3] Cornish, (1975).

[4] Bezhanishvili et al. (2010)

[5] Cornish, (1975). Bezhanishvili et al. (2010).

[6] Cornish, (1975). Bezhanishvili et al. (2010).

[7] Bezhanishvili et al. (2010).