
A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In the theory of Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.

Brigadier Ralph Alger Bagnold, OBE, FRS, was an English 20th-century desert explorer, geologist and soldier.
The Physics of Blown Sand and Desert Dunes is a scientific book written by Ralph A. Bagnold. The book laid the foundations of the scientific investigation of the transport of sand by wind. It also discusses the formation and movement of sand dunes in the Libyan Desert. During his expeditions into the Libyan Desert, Bagnold had been fascinated by the shapes of the sand dunes, and after returning to England he built a wind tunnel and conducted the experiments which are the basis of the book.

Terminal velocity is the maximum velocity (speed) attainable by an object as it falls through a fluid. It occurs when the sum of the drag force (Fd) and the buoyancy is equal to the downward force of gravity (FG) acting on the object. Since the net force on the object is zero, the object has zero acceleration. For objects falling through regular air, the buoyant force is usually dismissed and not taken into account as its effects are negligible
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations.

Aeolian processes, also spelled eolian, pertain to wind activity in the study of geology and weather and specifically to the wind's ability to shape the surface of the Earth. Winds may erode, transport, and deposit materials and are effective agents in regions with sparse vegetation, a lack of soil moisture and a large supply of unconsolidated sediments. Although water is a much more powerful eroding force than wind, aeolian processes are important in arid environments such as deserts.

A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact. The constituents that compose granular material are large enough such that they are not subject to thermal motion fluctuations. Thus, the lower size limit for grains in granular material is about 1 μm. On the upper size limit, the physics of granular materials may be applied to ice floes where the individual grains are icebergs and to asteroid belts of the Solar System with individual grains being asteroids.
Darcy's law is an equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on results of experiments on the flow of water through beds of sand, forming the basis of hydrogeology, a branch of earth sciences. It is analogous to Ohm's law in electrostatics, linearly relating the volume flow rate of the fluid to the hydraulic head difference via the hydraulic conductivity.

Soil mechanics is a branch of soil physics and applied mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids and other matter. Along with rock mechanics, soil mechanics provides the theoretical basis for analysis in geotechnical engineering, a subdiscipline of civil engineering, and engineering geology, a subdiscipline of geology. Soil mechanics is used to analyze the deformations of and flow of fluids within natural and man-made structures that are supported on or made of soil, or structures that are buried in soils. Example applications are building and bridge foundations, retaining walls, dams, and buried pipeline systems. Principles of soil mechanics are also used in related disciplines such as geophysical engineering, coastal engineering, agricultural engineering, hydrology and soil physics.
In fluid dynamics, drag is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers or between a fluid and a solid surface.

In geology, saltation is a specific type of particle transport by fluids such as wind or water. It occurs when loose materials are removed from a bed and carried by the fluid, before being transported back to the surface. Examples include pebble transport by rivers, sand drift over desert surfaces, soil blowing over fields, and snow drift over smooth surfaces such as those in the Arctic or Canadian Prairies.

Sediment transport is the movement of solid particles (sediment), typically due to a combination of gravity acting on the sediment, and the movement of the fluid in which the sediment is entrained. Sediment transport occurs in natural systems where the particles are clastic rocks, mud, or clay; the fluid is air, water, or ice; and the force of gravity acts to move the particles along the sloping surface on which they are resting. Sediment transport due to fluid motion occurs in rivers, oceans, lakes, seas, and other bodies of water due to currents and tides. Transport is also caused by glaciers as they flow, and on terrestrial surfaces under the influence of wind. Sediment transport due only to gravity can occur on sloping surfaces in general, including hillslopes, scarps, cliffs, and the continental shelf—continental slope boundary.
The maximum potential intensity of a tropical cyclone is the theoretical limit of the strength of a tropical cyclone.
Shear velocity, also called friction velocity, is a form by which a shear stress may be re-written in units of velocity. It is useful as a method in fluid mechanics to compare true velocities, such as the velocity of a flow in a stream, to a velocity that relates shear between layers of flow.

Stream power, originally derived by R. A. Bagnold in the 1960s, is the amount of energy the water in a river or stream is exerting on the sides and bottom of the river. Stream power is the result of multiplying the density of the water, the acceleration of the water due to gravity, the volume of water flowing through the river, and the slope of that water. There are many forms of the stream power formula with varying utilities, such as comparing rivers of various widths or quantifying the energy required to move sediment of a certain size. Stream power is closely related to other criteria such as stream competency and shear stress. Stream power is a valuable measurement for hydrologists and geomorphologists tackling sediment transport issues as well as for civil engineers, who use it in the planning and construction of roads, bridges, dams, and culverts.

In fluid mechanics, the Reynolds number is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers, flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow. These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation.

In hydrology stream competency, also known as stream competence, is a measure of the maximum size of particles a stream can transport. The particles are made up of grain sizes ranging from large to small and include boulders, rocks, pebbles, sand, silt, and clay. These particles make up the bed load of the stream. Stream competence was originally simplified by the “sixth-power-law,” which states the mass of a particle that can be moved is proportional to the velocity of the river raised to the sixth power. This refers to the stream bed velocity which is difficult to measure or estimate due to the many factors that cause slight variances in stream velocities.
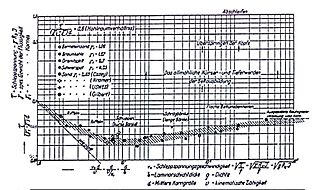
The Shields formula is a formula for the stability calculation of granular material in running water.















