
As originally stated in terms of direct-current resistive circuits only, Thévenin's theorem states that "For any linear electrical network containing only voltage sources, current sources and resistances can be replaced at terminals A–B by an equivalent combination of a voltage source Vth in a series connection with a resistance Rth."
A network, in the context of electrical engineering and electronics, is a collection of interconnected components. Network analysis is the process of finding the voltages across, and the currents through, all network components. There are many techniques for calculating these values. However, for the most part, the techniques assume linear components. Except where stated, the methods described in this article are applicable only to linear network analysis.
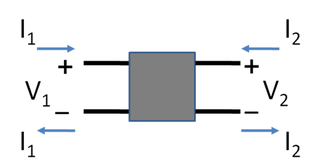
A two-port network is an electrical network (circuit) or device with two pairs of terminals to connect to external circuits. Two terminals constitute a port if the currents applied to them satisfy the essential requirement known as the port condition: the electric current entering one terminal must equal the current emerging from the other terminal on the same port. The ports constitute interfaces where the network connects to other networks, the points where signals are applied or outputs are taken. In a two-port network, often port 1 is considered the input port and port 2 is considered the output port.
This article illustrates some typical operational amplifier applications. A non-ideal operational amplifier's equivalent circuit has a finite input impedance, a non-zero output impedance, and a finite gain. A real op-amp has a number of non-ideal features as shown in the diagram, but here a simplified schematic notation is used, many details such as device selection and power supply connections are not shown. Operational amplifiers are optimised for use with negative feedback, and this article discusses only negative-feedback applications. When positive feedback is required, a comparator is usually more appropriate. See Comparator applications for further information.

In electronics, a current divider is a simple linear circuit that produces an output current (IX) that is a fraction of its input current (IT). Current division refers to the splitting of current between the branches of the divider. The currents in the various branches of such a circuit will always divide in such a way as to minimize the total energy expended.

An attenuator is an electronic device that reduces the power of a signal without appreciably distorting its waveform.
An all-pass filter is a signal processing filter that passes all frequencies equally in gain, but changes the phase relationship among various frequencies. Most types of filter reduce the amplitude of the signal applied to it for some values of frequency, whereas the all-pass filter allows all frequencies through without changes in level.

Electronic filter topology defines electronic filter circuits without taking note of the values of the components used but only the manner in which those components are connected.

Zobel networks are a type of filter section based on the image-impedance design principle. They are named after Otto Zobel of Bell Labs, who published a much-referenced paper on image filters in 1923. The distinguishing feature of Zobel networks is that the input impedance is fixed in the design independently of the transfer function. This characteristic is achieved at the expense of a much higher component count compared to other types of filter sections. The impedance would normally be specified to be constant and purely resistive. For this reason, Zobel networks are also known as constant resistance networks. However, any impedance achievable with discrete components is possible.

The Π pad is a specific type of attenuator circuit in electronics whereby the topology of the circuit is formed in the shape of the Greek letter "Π".
Image impedance is a concept used in electronic network design and analysis and most especially in filter design. The term image impedance applies to the impedance seen looking into a port of a network. Usually a two-port network is implied but the concept can be extended to networks with more than two ports. The definition of image impedance for a two-port network is the impedance, Zi 1, seen looking into port 1 when port 2 is terminated with the image impedance, Zi 2, for port 2. In general, the image impedances of ports 1 and 2 will not be equal unless the network is symmetrical with respect to the ports.
Dual impedance and dual network are terms used in electronic network analysis. The dual of an impedance is its reciprocal, or algebraic inverse . For this reason the dual impedance is also called the inverse impedance. Another way of stating this is that the dual of is the admittance .

A lattice phase equaliser or lattice filter is an example of an all-pass filter. That is, the attenuation of the filter is constant at all frequencies but the relative phase between input and output varies with frequency. The lattice filter topology has the particular property of being a constant-resistance network and for this reason is often used in combination with other constant resistance filters such as bridge-T equalisers. The topology of a lattice filter, also called an X-section is identical to bridge topology. The lattice phase equaliser was invented by Otto Zobel. using a filter topology proposed by George Campbell.

The bridged-T delay equaliser is an electrical all-pass filter circuit utilising bridged-T topology whose purpose is to insert an (ideally) constant delay at all frequencies in the signal path. It is a class of image filter.
An equivalent impedance is an equivalent circuit of an electrical network of impedance elements which presents the same impedance between all pairs of terminals as did the given network. This article describes mathematical transformations between some passive, linear impedance networks commonly found in electronic circuits.
An antimetric electrical network is an electrical network that exhibits anti-symmetrical electrical properties. The term is often encountered in filter theory, but it applies to general electrical network analysis. Antimetric is the diametrical opposite of symmetric; it does not merely mean "asymmetric". It is possible for networks to be symmetric or antimetric in their electrical properties without being physically or topologically symmetric or antimetric.
The Miller theorem refers to the process of creating equivalent circuits. It asserts that a floating impedance element, supplied by two voltage sources connected in series, may be split into two grounded elements with corresponding impedances. There is also a dual Miller theorem with regards to impedance supplied by two current sources connected in parallel. The two versions are based on the two Kirchhoff's circuit laws.

The T pad is a specific type of attenuator circuit in electronics whereby the topology of the circuit is formed in the shape of the letter "T".

In electrical circuit theory, a port is a pair of terminals connecting an electrical network or circuit to an external circuit, as a point of entry or exit for electrical energy. A port consists of two nodes (terminals) connected to an outside circuit which meets the port condition - the currents flowing into the two nodes must be equal and opposite.
A symmetrical lattice is a two-port electrical wave filter in which diagonally-crossed shunt elements are present – a configuration which sets it apart from ladder networks. The component arrangement of the lattice is shown in the diagram below. The filter properties of this circuit were first developed using image impedance concepts, but later the more general techniques of network analysis were applied to it.























