
In physics and electrical engineering, a cutoff frequency, corner frequency, or break frequency is a boundary in a system's frequency response at which energy flowing through the system begins to be reduced rather than passing through.

In optics, a Gaussian beam is a beam of electromagnetic radiation with high monochromaticity whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or TEM00) transverse Gaussian mode describes the intended output of most (but not all) lasers, as such a beam can be focused into the most concentrated spot. When such a beam is refocused by a lens, the transverse phase dependence is altered; this results in a different Gaussian beam. The electric and magnetic field amplitude profiles along any such circular Gaussian beam (for a given wavelength and polarization) are determined by a single parameter: the so-called waist w0. At any position z relative to the waist (focus) along a beam having a specified w0, the field amplitudes and phases are thereby determined as detailed below.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source. Even when there is a propagating electromagnetic wave produced, one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths.
Fourier optics is the study of classical optics using Fourier transforms (FTs), in which the waveform being considered is regarded as made up of a combination, or superposition, of plane waves. It has some parallels to the Huygens–Fresnel principle, in which the wavefront is regarded as being made up of a combination of spherical wavefronts whose sum is the wavefront being studied. A key difference is that Fourier optics considers the plane waves to be natural modes of the propagation medium, as opposed to Huygens–Fresnel, where the spherical waves originate in the physical medium.

The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
A transverse mode of electromagnetic radiation is a particular electromagnetic field pattern of the radiation in the plane perpendicular to the radiation's propagation direction. Transverse modes occur in radio waves and microwaves confined to a waveguide, and also in light waves in an optical fiber and in a laser's optical resonator.
Geometrical optics, or ray optics, is a model of optics that describes light propagation in terms of rays. The ray in geometrical optics is an abstraction useful for approximating the paths along which light propagates under certain circumstances.
In optics, an ultrashort pulse, also known as an ultrafast event, is an electromagnetic pulse whose time duration is of the order of a picosecond or less. Such pulses have a broadband optical spectrum, and can be created by mode-locked oscillators. Amplification of ultrashort pulses almost always requires the technique of chirped pulse amplification, in order to avoid damage to the gain medium of the amplifier.

In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic, cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.

Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers.
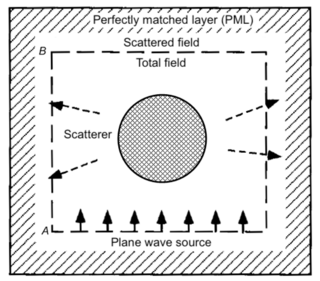
A perfectly matched layer (PML) is an artificial absorbing layer for wave equations, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries, especially in the FDTD and FE methods. The key property of a PML that distinguishes it from an ordinary absorbing material is that it is designed so that waves incident upon the PML from a non-PML medium do not reflect at the interface—this property allows the PML to strongly absorb outgoing waves from the interior of a computational region without reflecting them back into the interior.
In numerical analysis, the split-step (Fourier) method is a pseudo-spectral numerical method used to solve nonlinear partial differential equations like the nonlinear Schrödinger equation. The name arises for two reasons. First, the method relies on computing the solution in small steps, and treating the linear and the nonlinear steps separately. Second, it is necessary to Fourier transform back and forth because the linear step is made in the frequency domain while the nonlinear step is made in the time domain.
In optics, the term soliton is used to refer to any optical field that does not change during propagation because of a delicate balance between nonlinear and dispersive effects in the medium. There are two main kinds of solitons:

In fluid dynamics, the Boussinesq approximation for water waves is an approximation valid for weakly non-linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by John Scott Russell of the wave of translation. The 1872 paper of Boussinesq introduces the equations now known as the Boussinesq equations.

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
Eigenmode expansion (EME) is a computational electrodynamics modelling technique. It is also referred to as the mode matching technique or the bidirectional eigenmode propagation method. Eigenmode expansion is a linear frequency-domain method.
Geometrical acoustics or ray acoustics is a branch of acoustics that studies propagation of sound on the basis of the concept of acoustic rays, defined as lines along which the acoustic energy is transported. This concept is similar to geometrical optics, or ray optics, that studies light propagation in terms of optical rays. Geometrical acoustics is an approximate theory, valid in the limiting case of very small wavelengths, or very high frequencies. The principal task of geometrical acoustics is to determine the trajectories of sound rays. The rays have the simplest form in a homogeneous medium, where they are straight lines. If the acoustic parameters of the medium are functions of spatial coordinates, the ray trajectories become curvilinear, describing sound reflection, refraction, possible focusing, etc. The equations of geometric acoustics have essentially the same form as those of geometric optics. The same laws of reflection and refraction hold for sound rays as for light rays. Geometrical acoustics does not take into account such important wave effects as diffraction. However, it provides a very good approximation when the wavelength is very small compared to the characteristic dimensions of inhomogeneous inclusions through which the sound propagates.
In physics and mathematics, the spacetime triangle diagram (STTD) technique, also known as the Smirnov method of incomplete separation of variables, is the direct space-time domain method for electromagnetic and scalar wave motion.

A frequency-selective surface (FSS) is any thin, repetitive surface designed to reflect, transmit or absorb electromagnetic fields based on the frequency of the field. In this sense, an FSS is a type of optical filter or metal-mesh optical filters in which the filtering is accomplished by virtue of the regular, periodic pattern on the surface of the FSS. Though not explicitly mentioned in the name, FSS's also have properties which vary with incidence angle and polarization as well - these are unavoidable consequences of the way in which FSS's are constructed. Frequency-selective surfaces have been most commonly used in the radio frequency region of the electromagnetic spectrum and find use in applications as diverse as the aforementioned microwave oven, antenna radomes and modern metamaterials. Sometimes frequency selective surfaces are referred to simply as periodic surfaces and are a 2-dimensional analog of the new periodic volumes known as photonic crystals.
















