Bender's method

Last updated

In group theory, Bender's method is a method introduced by Bender (1970) for simplifying the local group theoretic analysis of the odd order theorem. Shortly afterwards he used it to simplify the Walter theorem on groups with abelian Sylow 2-subgroups Bender (1970b), and Gorenstein and Walter's classification of groups with dihedral Sylow 2-subgroups. Bender's method involves studying a maximal subgroup M containing the centralizer of an involution, and its generalized Fitting subgroup F*(M).

One succinct version of Bender's method is the result that if M, N are two distinct maximal subgroups of a simple group with F*(M) ≤ N and F*(N) ≤ M, then there is a prime p such that both F*(M) and F*(N) are p-groups. This situation occurs whenever M and N are distinct maximal parabolic subgroups of a simple group of Lie type, and in this case p is the characteristic, but this has only been used to help identify groups of low Lie rank. These ideas are described in textbook form in Gagen (1976 , p. 43), Huppert & Blackburn (1982 , Chapter X. 15), Gorenstein, Lyons & Solomon (1996 , p. 110, Chapter F.19), and Kurzweil & Stellmacher (2004 , Chapter 10.1).

Related Research Articles

<span class="mw-page-title-main">Classification of finite simple groups</span> Massive theorem assigning all but 27 finite simple groups to a few infinite families

In mathematics, the classification of finite simple groups is a result of group theory stating that every finite simple group is either cyclic, or alternating, or it belongs to a broad infinite class called the groups of Lie type, or else it is one of twenty-six or twenty-seven exceptions, called sporadic. The proof consists of tens of thousands of pages in several hundred journal articles written by about 100 authors, published mostly between 1955 and 2004.

<span class="texhtml mvar" style="font-style:italic;">p</span>-group Group in which the order of every element is a power of p

In mathematics, specifically group theory, given a prime number p, a p-group is a group in which the order of every element is a power of p. That is, for each element g of a p-group G, there exists a nonnegative integer n such that the product of pn copies of g, and not fewer, is equal to the identity element. The orders of different elements may be different powers of p.

<span class="mw-page-title-main">Simple group</span> Group without normal subgroups other than the trivial group and itself

In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, namely a nontrivial normal subgroup and the corresponding quotient group. This process can be repeated, and for finite groups one eventually arrives at uniquely determined simple groups, by the Jordan–Hölder theorem.

<span class="mw-page-title-main">Sylow theorems</span> Theorems that help decompose a finite group based on prime factors of its order

In mathematics, specifically in the field of finite group theory, the Sylow theorems are a collection of theorems named after the Norwegian mathematician Peter Ludwig Sylow that give detailed information about the number of subgroups of fixed order that a given finite group contains. The Sylow theorems form a fundamental part of finite group theory and have very important applications in the classification of finite simple groups.

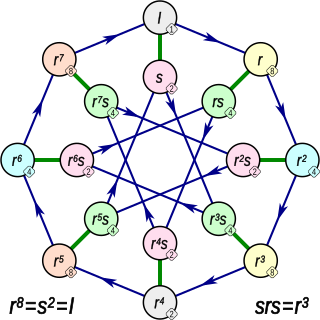
<span class="mw-page-title-main">Quasidihedral group</span>

In mathematics, the quasi-dihedral groups, also called semi-dihedral groups, are certain non-abelian groups of order a power of 2. For every positive integer n greater than or equal to 4, there are exactly four isomorphism classes of non-abelian groups of order 2n which have a cyclic subgroup of index 2. Two are well known, the generalized quaternion group and the dihedral group. One of the remaining two groups is often considered particularly important, since it is an example of a 2-group of maximal nilpotency class. In Bertram Huppert's text Endliche Gruppen, this group is called a "Quasidiedergruppe". In Daniel Gorenstein's text, Finite Groups, this group is called the "semidihedral group". Dummit and Foote refer to it as the "quasidihedral group"; we adopt that name in this article. All give the same presentation for this group:

In mathematics, especially in the area of algebra known as group theory, the Fitting subgroupF of a finite group G, named after Hans Fitting, is the unique largest normal nilpotent subgroup of G. Intuitively, it represents the smallest subgroup which "controls" the structure of G when G is solvable. When G is not solvable, a similar role is played by the generalized Fitting subgroupF*, which is generated by the Fitting subgroup and the components of G.

In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by Walter Feit and John Griggs Thompson.

In mathematics, in the area of abstract algebra known as group theory, an A-group is a type of group that is similar to abelian groups. The groups were first studied in the 1940s by Philip Hall, and are still studied today. A great deal is known about their structure.

In mathematical finite group theory, the Thompson subgroup of a finite p-group P refers to one of several characteristic subgroups of P. John G. Thompson (1964) originally defined to be the subgroup generated by the abelian subgroups of P of maximal rank. More often the Thompson subgroup is defined to be the subgroup generated by the abelian subgroups of P of maximal order or the subgroup generated by the elementary abelian subgroups of P of maximal rank. In general these three subgroups can be different, though they are all called the Thompson subgroup and denoted by .

In mathematics, the Alperin–Brauer–Gorenstein theorem characterizes the finite simple groups with quasidihedral or wreathed Sylow 2-subgroups. These are isomorphic either to three-dimensional projective special linear groups or projective special unitary groups over a finite field of odd order, depending on a certain congruence, or to the Mathieu group . Alperin, Brauer & Gorenstein (1970) proved this in the course of 261 pages. The subdivision by 2-fusion is sketched there, given as an exercise in Gorenstein, and presented in some detail in Kwon et al. (1980).

In mathematics, George Glauberman's ZJ theorem states that if a finite group G is p-constrained and p-stable and has a normal p-subgroup for some odd prime p, then Op′(G)Z(J(S)) is a normal subgroup of G, for any Sylow p-subgroupS.

In abstract algebra, the focal subgroup theorem describes the fusion of elements in a Sylow subgroup of a finite group. The focal subgroup theorem was introduced in and is the "first major application of the transfer" according to. The focal subgroup theorem relates the ideas of transfer and fusion such as described in. Various applications of these ideas include local criteria for p-nilpotence and various non-simplicity criteria focussing on showing that a finite group has a normal subgroup of index p.

In mathematics, a signalizer functor gives the intersections of a potential subgroup of a finite group with the centralizers of nontrivial elements of an abelian group. The signalizer functor theorem gives conditions under which a signalizer functor comes from a subgroup. The idea is to try to construct a -subgroup of a finite group , which has a good chance of being normal in , by taking as generators certain -subgroups of the centralizers of nonidentity elements in one or several given noncyclic elementary abelian -subgroups of The technique has origins in the Feit–Thompson theorem, and was subsequently developed by many people including Gorenstein (1969) who defined signalizer functors, Glauberman (1976) who proved the Solvable Signalizer Functor Theorem for solvable groups, and McBride who proved it for all groups. This theorem is needed to prove the so-called "dichotomy" stating that a given nonabelian finite simple group either has local characteristic two, or is of component type. It thus plays a major role in the classification of finite simple groups.

In mathematical finite group theory, an N-group is a group all of whose local subgroups are solvable groups. The non-solvable ones were classified by Thompson during his work on finding all the minimal finite simple groups.

In mathematics, the Walter theorem, proved by John H. Walter, describes the finite groups whose Sylow 2-subgroup is abelian. Bender (1970) used Bender's method to give a simpler proof.

In finite group theory, a branch of mathematics, a group is said to be of characteristic 2 type or even type or of even characteristic if it resembles a group of Lie type over a field of characteristic 2.

In mathematical finite group theory, the Gorenstein–Harada theorem, proved by Gorenstein and Harada in a 464-page paper, classifies the simple finite groups of sectional 2-rank at most 4. It is part of the classification of finite simple groups.

In finite group theory, a p-stable group for an odd prime p is a finite group satisfying a technical condition introduced by Gorenstein and Walter in order to extend Thompson's uniqueness results in the odd order theorem to groups with dihedral Sylow 2-subgroups.

In mathematical finite group theory, the Thompson transitivity theorem gives conditions under which the centralizer of an abelian subgroup A acts transitively on certain subgroups normalized by A. It originated in the proof of the odd order theorem by Feit and Thompson (1963), where it was used to prove the Thompson uniqueness theorem.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.