Beurling algebra

Last updated March 14, 2019

In mathematics, the term Beurling algebra is used for different algebras introduced by ArneBeurling ( 1949 ), usually it is an algebra of periodic functions with Fourier series

Arne Carl-August Beurling was a Swedish mathematician and professor of mathematics at Uppsala University (1937–1954) and later at the Institute for Advanced Study in Princeton, New Jersey. Beurling worked extensively in harmonic analysis, complex analysis and potential theory. The "Beurling factorization" helped mathematical scientists to understand the Wold decomposition, and inspired further work on the invariant subspaces of linear operators and operator algebras, e.g. Håkan Hedenmalm's factorization theorem for Bergman spaces.

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of 2π radians. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called aperiodic.

In mathematics, a Fourier series is a way to represent a function as the sum of simple sine waves. More formally, it decomposes any periodic function or periodic signal into the weighted sum of a set of simple oscillating functions, namely sines and cosines.

f(x)=\sum a_{n}e^{inx}

Example We may consider the algebra of those functions f where the majorants

c_{k}=\sup _{|n|\geq k}|a_{n}|

of the Fourier coefficients a_n are summable. In other words

\sum _{k\geq 0}c_{k}<\infty .

Example We may consider a weight function w on $\mathbb {Z}$ such that

w(m+n)\leq w(m)w(n),\quad w(0)=1

in which case $A_{w}(\mathbb {T} )=\{f:f(t)=\sum _{n}a_{n}e^{int},\,\|f\|_{w}=\sum _{n}|a_{n}|w(n)<\infty \}\,(\sim \ell _{w}^{1}(\mathbb {Z} ))$ is a unitary commutative Banach algebra.

In mathematics, the unitary group of degree n, denoted U(n), is the group of n × n unitary matrices, with the group operation of matrix multiplication. The unitary group is a subgroup of the general linear group GL(n, C). Hyperorthogonal group is an archaic name for the unitary group, especially over finite fields. For the group of unitary matrices with determinant 1, see Special unitary group.

In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers that at the same time is also a Banach space, i.e. a normed space and complete in the metric induced by the norm. The norm is required to satisfy

These algebras are closely related to the Wiener algebra.

In mathematics, the Wiener algebra, named after Norbert Wiener and usually denoted by $A (T)$ , is the space of absolutely convergent Fourier series. Here $T$ denotes the circle group.

Related Research Articles

In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. Thus, for instance, 6 is the product of 2 and 3, and $is the product of and .$

In mathematics, real analysis is the branch of mathematical analysis that studies the behavior of real numbers, sequences and series of real numbers, and real-valued functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.

In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions $converges uniformly to a limiting function on a set if, given any arbitrarily small positive number, a number can be found such that each of the functions differ from by no more than at every point in . Described in an informal way, if converges to uniformly, then the rate at which approaches is "uniform" throughout its domain in the following sense: in order to determine how large needs to be to guarantee that falls within a certain distance of, we do not need to know the value of in question — there is a single value of independent of, such that choosing to be larger than will suffice.$

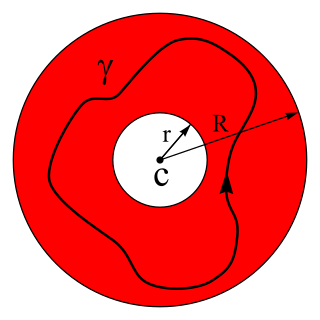
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.

In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.

In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field. In its basic form, it asserts that for a family of continuous linear operators whose domain is a Banach space, pointwise boundedness is equivalent to uniform boundedness in operator norm.

In mathematics, Fatou's lemma establishes an inequality relating the Lebesgue integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions. The lemma is named after Pierre Fatou.

In complex analysis, the Hardy spacesH^p are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz, who named them after G. H. Hardy, because of the paper. In real analysis Hardy spaces are certain spaces of distributions on the real line, which are boundary values of the holomorphic functions of the complex Hardy spaces, and are related to the L^p spaces of functional analysis. For 1 ≤ p ≤ ∞ these real Hardy spaces H^p are certain subsets of L^p, while for p < 1 the L^p spaces have some undesirable properties, and the Hardy spaces are much better behaved.

In mathematics, more specifically in harmonic analysis, Walsh functions form a complete orthogonal set of functions that can be used to represent any discrete function—just like trigonometric functions can be used to represent any continuous function in Fourier analysis. They can thus be viewed as a discrete, digital counterpart of the continuous, analog system of trigonometric functions on the unit interval. But unlike the sine and cosine functions, which are continuous, Walsh functions are piecewise constant. They take the values −1 and +1 only, on sub-intervals defined by dyadic fractions.

In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol. Occasionally, the term multiplier operator itself is shortened simply to multiplier. In simple terms, the multiplier reshapes the frequencies involved in any function. This class of operators turns out to be broad: general theory shows that a translation-invariant operator on a group which obeys some regularity conditions can be expressed as a multiplier operator, and conversely. Many familiar operators, such as translations and differentiation, are multiplier operators, although there are many more complicated examples such as the Hilbert transform.

In mathematics, the Riemann–Lebesgue lemma, named after Bernhard Riemann and Henri Lebesgue, is of importance in harmonic analysis and asymptotic analysis.

In mathematics, there are usually many different ways to construct a topological tensor product of two topological vector spaces. For Hilbert spaces or nuclear spaces there is a simple well-behaved theory of tensor products, but for general Banach spaces or locally convex topological vector spaces the theory is notoriously subtle.

Inequalities are very important in the study of information theory. There are a number of different contexts in which these inequalities appear.

In linear algebra, a subset of the vectors $of a Banach space, sometimes called a "system", is complete if every element in can be approximated arbitrarily well in norm by finite linear combinations of elements in . Such a complete system is overcomplete if removal of a from the system results in a system that is still complete. In different research, such as signal processing and function approximation, overcompleteness can help researchers to achieve a more stable, more robust, or more compact decomposition than using a basis. Overcomplete frames are widely used in mathematics, computer science, engineering, and statistics.$

In mathematical analysis, Lorentz spaces, introduced by George Lorentz in the 1950s, are generalisations of the more familiar $spaces$ .

In mathematics, a summability kernel is a family or sequence of periodic integrable functions satisfying a certain set of properties, listed below. Certain kernels, such as the Fejér kernel, are particularly useful in Fourier analysis. Summability kernels are related to approximation of the identity; definitions of an approximation of identity vary, but sometimes the definition of an approximation of the identity is taken to be the same as for a summability kernel.

In mathematics, the Weil–Brezin map, named after André Weil and Jonathan Brezin, is a unitary transformation that maps a Schwartz function on the real line to a smooth function on the Heisenberg manifold. The Weil–Brezin map gives a geometric interpretation of the Fourier transform, the Plancherel theorem and the Poisson summation formula. The image of Gaussian functions under the Weil–Brezin map are nil-theta functions, which are related to theta functions. The Weil–Brezin map is sometimes referred to as the Zak transform, which is widely applied in the field of physics and signal processing; however, the Weil–Brezin Map is defined via Heisenberg group geometrically, whereas there is no direct geometric or group theoretic interpretation from the Zak transform.

In mathematics, moduli of smoothness are used to quantitatively measure smoothness of functions. Moduli of smoothness generalise modulus of continuity and are used in approximation theory and numerical analysis to estimate errors of approximation by polynomials and splines.

References

Belinsky, E.S.; Liflyand, E.R. (2001) [1994], "B/b130120", in Hazewinkel, Michiel, Encyclopedia of Mathematics , Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
Beurling, Arne (1949), "On the spectral synthesis of bounded functions", Acta Math., 81 (1): 225–238, doi:10.1007/BF02395018, MR 0027891

Michiel Hazewinkel is a Dutch mathematician, and Emeritus Professor of Mathematics at the Centre for Mathematics and Computer and the University of Amsterdam, particularly known for his 1978 book Formal groups and applications and as editor of the Encyclopedia of Mathematics.

The Encyclopedia of Mathematics is a large reference work in mathematics. It is available in book form and on CD-ROM.

International Standard Book Number Unique numeric book identifier

The International Standard Book Number (ISBN) is a numeric commercial book identifier which is intended to be unique. Publishers purchase ISBNs from an affiliate of the International ISBN Agency.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.