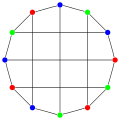
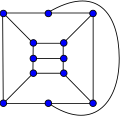
| Bidiakis cube | |
|---|---|
 The Bidiakis cube | |
| Vertices | 12 |
| Edges | 18 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 4 |
| Automorphisms | 8 (D4) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Cubic Hamiltonian Triangle-free Polyhedral Planar |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Bidiakis cube is a 3-regular graph with 12 vertices and 18 edges. [1]
The Bidiakis cube is a cubic Hamiltonian graph and can be defined by the LCF notation [-6,4,-4]4.
The Bidiakis cube can also be constructed from a cube by adding edges across the top and bottom faces which connect the centres of opposite sides of the faces. The two additional edges need to be perpendicular to each other. With this construction, the Bidiakis cube is a polyhedral graph, and can be realized as a convex polyhedron. Therefore, by Steinitz's theorem, it is a 3-vertex-connected simple planar graph. [2] [3]
The Bidiakis cube is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 8, the group of symmetries of a square, including both rotations and reflections.
The characteristic polynomial of the Bidiakis cube is .
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.
In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells.
In solid geometry, a face is a flat (planar) surface that forms part of the boundary of a solid object; a three-dimensional solid bounded exclusively by faces is a polyhedron.
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.
In geometry, the rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
In the mathematical field of graph theory, a snark is a simple, connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, the connectivity is redundant so that removing no one edge would split the graph, and the edges cannot be colored by only three colors without two edges of the same color meeting at a point. In order to avoid trivial cases, snarks are often restricted to have girth at least 5.
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.
In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge whenever two faces of G are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
In the mathematical field of graph theory, the butterfly graph is a planar undirected graph with 5 vertices and 6 edges. It can be constructed by joining 2 copies of the cycle graph C3 with a common vertex and is therefore isomorphic to the friendship graph F2.
In geometry, a vertex, often denoted by letters such as , , , , is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.
In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope. In a polygon, an edge is a line segment on the boundary, and is often called a side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces meet. A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal.
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”
In the mathematical field of graph theory, the Frucht graph is a 3-regular graph with 12 vertices, 18 edges, and no nontrivial symmetries. It was first described by Robert Frucht in 1939.
In the mathematical field of graph theory, the Tutte graph is a 3-regular graph with 46 vertices and 69 edges named after W. T. Tutte. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8.
In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected planar graphs.
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges, the smallest non-Hamiltonian polyhedral graph. It is named after British astronomer Alexander Stewart Herschel.
In the mathematical field of graph theory, the Goldner–Harary graph is a simple undirected graph with 11 vertices and 27 edges. It is named after A. Goldner and Frank Harary, who proved in 1975 that it was the smallest non-Hamiltonian maximal planar graph. The same graph had already been given as an example of a non-Hamiltonian simplicial polyhedron by Branko Grünbaum in 1967.
In the mathematical field of graph theory, a prism graph is a graph that has one of the prisms as its skeleton.
In graph theory, the Golomb graph is a polyhedral graph with 10 vertices and 18 edges. It is named after Solomon W. Golomb, who constructed it as a unit distance graph that requires four colors in any graph coloring. Thus, like the simpler Moser spindle, it provides a lower bound for the Hadwiger–Nelson problem: coloring the points of the Euclidean plane so that each unit line segment has differently-colored endpoints requires at least four colors.
 | Wikimedia Commons has media related to Bidiakis cube . |
